| Α.7.5 Πολλαπλασιασμός ρητών αριθμών |
| |
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ |
 |
Ένας έμπορος διαπίστωσε, ότι κάθε ημέρα του τελευταίου δεκαήμερου των εκπτώσεων έβγαζε κέρδος 524,5€. Το επόμενο, όμως, δεκαήμερο είχε καθημερινή ζημιά 265,4€.
Είναι γνωστό, ότι στα λογιστικά βιβλία το κέρδος καταχωρείται ως θετική εγγραφή και η ζημιά ως αρνητική.
Δηλαδή, το συνολικό κέρδος για το δεκαήμερο των εκπτώσεων θα είναι (+524,5€) · (+10 ημέρες) και για το επόμενο δεκαήμερο η συνολική ζημιά θα είναι (-265,4€) · (+10 ημέρες)
- Προσπάθησε να βρεις το αποτέλεσμα των παραπάνω πράξεων χωρίς να κάνεις τους πολλαπλασιασμούς.
- Τι παρατηρείς για το πρόσημο των αποτελεσμάτων;
|
 |
|
|
| |
 |
Διαπιστώνουμε, λοιπόν, ότι:
- Το γινόμενο δύο θετικών ρητών είναι θετικός ρητός
- Το γινόμενο ενός θετικού και ενός αρνητικού ρητού είναι αρνητικός ρητός
|
Μικροπείραμα  |
| Ας δούμε τώρα πώς βρίσκουμε το γινόμενο δύο αρνητικών ακεραίων. |
| (-10) · (+9) = -90 |
|
|
| (-10) · (+8) = -80 |
|
Σημειώνουμε τους πολλαπλασιασμούς δύο παραγόντων, |
| (-10) · (+7) = -70 |
|
από τους οποίους ο ένας μένει σταθερός, το -10, και ο |
| (-10) · (+6) = -60 |
|
άλλος μειώνεται διαδοχικά κατά 1 κάθε φορά. |
| (-10) · (+5) = -50 |
|
|
| (-10) · (+4) = -40 |
|
Παρατηρούμε ότι τα γινόμενα αυξάνονται διαδοχικά κατά 10 |
| (-10) · (+3) = -30 |
|
|
| (-10) · (+2) = -20 |
|
Αν υποθέσουμε ότι και μετά το μηδενισμό του δεύτερου |
| (-10) · (+1) = -10 |
|
παράγοντα τα γινόμενα συνεχίζουν να αυξάνονται με τον |
| (-10) · 0 = 0 |
|
ίδιο τρόπο, πρέπει να ορίσουμε ότι: |
| (-10) · (-1) = ; |
|
(-10) · (-1) = +10 = +(10 · 1) |
| (-10) · (-2) = ; |
|
(-10) · (-2) = +20 = +(10 · 2) |
| (-10) · (-3) = ; |
|
(-10) · (-3) = +30 = +(10 · 3) |
| (-10) · (-4) = ; |
|
(-10) · (-4) = +40 = +(10 · 4) |
| ......................... |
|
.............................................. |
|
 |
Διαπιστώνουμε, επομένως, ότι:
- Το γινόμενο δύο αρνητικών ακεραίων είναι θετικός ακέραιος
Γενικότερα:
- Το γινόμενο δύο αρνητικών ρητών είναι θετικός ρητός.
|
|
Προσομοίωση  |
|
|
 |
Ιδιότητες τoυ πολλαπλασιασμού
| Παρατηρούμε ότι: |
Γενικά ισχύει ότι: |
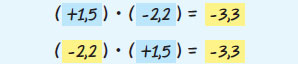 |
- Αντιμεταθετική ιδιότητα
(Μπορούμε να αλλάζουμε τη σειρά δύο παραγόντων ενός γινομένου)
|
 |
| α · (β · γ) = (α · β) · γ |
|
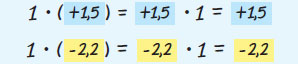 |
- Το γινόμενο ενός ρητού αριθμού με τη μονάδα ισούται με τον ίδιο τον αριθμό.
|
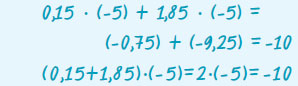 |
- Επιμεριστική ιδιότητα του πολλαπλασιασμού ως προς την πρόσθεση και την αφαίρεση:
| α · (β + γ) = α · β + α · γ και α · (β - γ) = α · β - α · γ |
|
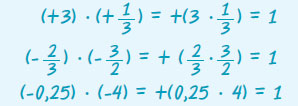 |
- Οι ρητοί αριθμοί α και β λέγονται αντίστροφοι, όταν είναι διάφοροι του μηδενός και το γινόμενό τους είναι ίσο με τη μονάδα:
Ο καθένας από τους α και β είναι αντίστροφος του άλλου. |
 |
- Το γινόμενο ενός ρητού αριθμού επί το μηδέν
ισούται με το μηδέν.
|
|
| |
Γινόμενο πολλών παραγόντων
Πώς εργαζόμαστε όταν έχουμε να υπολογίσουμε ένα γινόμενο με περισσότερους από δύο παράγοντες;
Γνωρίζουμε ότι το γινόμενο θετικών ρητών είναι πάντα θετικό. Αν υπάρχει ένας παράγοντας που είναι αρνητικός μετατρέπει το γινόμενο σε αρνητικό. Στην περίπτωση που υπάρχει και δεύτερος αρνητικός παράγοντας ξαναμετατρέπει το γινόμενο σε θετικό κ.ο.κ.
Άρα:
- Για να υπολογίσουμε ένα γινόμενο πολλών παραγόντων (που κανένας δεν είναι μηδέν), πολλαπλασιάζουμε τις απόλυτες τιμές τους και στο γινόμενο βάζουμε:
- Το πρόσημο +, αν το πλήθος των αρνητικών παραγόντων είναι άρτιο (ζυγό).
- Το πρόσημο -, αν το πλήθος των αρνητικών παραγόντων είναι περιττό (μονό).
- Αν τουλάχιστον ένας παράγοντας είναι μηδέν, τότε και το γινόμενο είναι ίσο με μηδέν
Το σημείο του πολλαπλασιασμού «.» μεταξύ των γραμμάτων και των παρενθέσεων παραλείπεται. |
| |
| ΠΑΡΑΔΕΙΓΜΑΤΑ - ΕΦΑΡΜΟΓΕΣ |
|
| |
| ΑΣΚΗΣΕΙΣ ΚΑΙ ΠΡΟΒΛΗΜΑΤΑ |
|
Να συμπληρωθούν τα παρακάτω κενά:
α) Το πρόσημο του γινομένου δύο ομόσημων ρητών είναι πάντα ............................................................ .
(β) Το πρόσημο του γινομένου δύο ετερόσημων ρητών είναι πάντα ......................................................................... .
(γ) Ένας ρητός όταν πολλαπλασιάζεται με το 1 δεν ................................................................................................. .
(δ) Το γινόμενο δύο αντίστροφων αριθμών είναι πάντα ίσο με................................................................................... .
(ε) Το πρόσημο γινομένου πολλών παραγόντων εξαρτάται από το πλήθος των ............................................. παραγόντων. |
 |
 |
Υπολόγισε τα γινόμενα: (α) (-1)(-1), (β) -3(-10), (γ) -1,2(-0,5), (δ) 0(-10589), 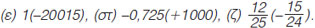
Μικροπείραμα  |
 |
Υπολόγισε την τιμή των παραστάσεων με τις λιγότερες δυνατές πράξεις:
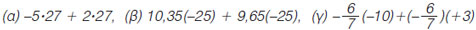
|
 |
| Συμπλήρωσε τον πίνακα: |
| • |
-1 |
-$\dfrac{1}{2}$ |
0 |
+2 |
+3 |
| -2 |
|
|
|
|
|
| -3,2 |
|
|
|
|
|
| +$\dfrac{3}{2}$ |
|
|
|
|
|
| +10 |
|
|
|
|
|
Άσκηση  |
|
 |
Κάνε τις πράξεις: 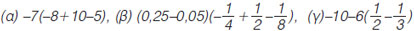 |
 |
Κάνε τις πράξεις: (α) (5+α)(2+β), (β) (α+7)(α-7), (γ) (α-3)(β-3), (δ) (γ+8)(δ+5). |
 |
Υπολόγισε τα γινόμενα: (α) (-1)(-1), (β) (-1)(-1)(-1), (γ) (-1)(-1)(-1)(-1) |
 |
Υπολόγισε την τιμή των παραστάσεων:
Α = (α-1)(α+1)(α-2)(α+2), |
|
όταν α = 3 |
| B = β(β-3)(β+3)(β-5)(β+5), |
|
όταν β = 2 |
| Γ = γ(2γ-1)(3γ+1)(4γ-2)(γ+2)(γ-2), |
|
όταν γ=0,5 |
|
 |
| Συμπλήρωσε τον πίνακα: |
| x |
y |
z |
ω |
A=xyz |
B=yxω |
Γ=xA-B |
AB+Γ |
| -2 |
0,5 |
+1 |
-3 |
|
|
|
|
| -$\dfrac{1}{2}$ |
+6 |
-4 |
-0,3 |
|
|
|
|
| -2 |
+$\dfrac{3}{2}$ |
0,2 |
-7 |
|
|
|
|
|
|
|
|