| Α.7.4. Αφαίρεση ρητών αριθμών |
| |
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ |
 |
Στο σχήμα βλέπουμε τη μέση θερμοκρασία μιας περιοχής για τους 12 μήνες του χρόνου σε συγκεκριμένη ώρα της ημέρας.
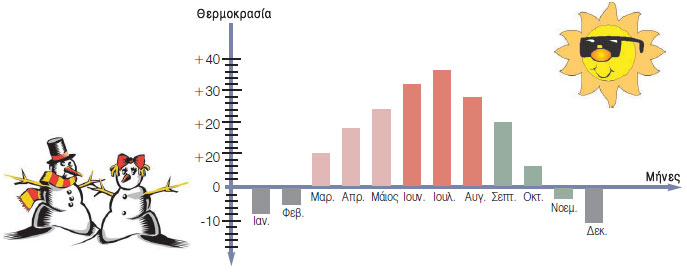
Ποιος είναι ο πιο ζεστός μήνας του έτους και ποιος ο πιο κρύος;
Ποια είναι η διαφορά θερμοκρασίας μεταξύ αυτών των μηνών;
Ποια είναι η διαφορά θερμοκρασίας μεταξύ κάθε δύο διαδοχικών μηνών; |
|
Προσομοίωση 1 Προσομοίωση 2 Προσομοίωση 2 |
|
 |
Για να αφαιρέσουμε από τον αριθμό α τον αριθμό β, προσθέτουμε στον α τον αντίθετο του β.
|
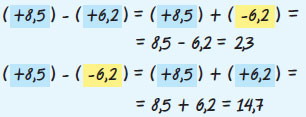 |
Στους ρητούς αριθμούς η αφαίρεση μετατρέπεται σε πρόσθεση και επομένως είναι πάντα δυνατή (δηλαδή, δεν απαιτείται να είναι ο μειωτέος πάντα μεγαλύτερος από τον αφαιρετέο, όπως ίσχυε μέχρι τώρα). |
|
Απαλοιφή παρενθέσεων
Σε αρκετές περιπτώσεις αριθμητικών παραστάσεων εμφανίζονται περισσότεροι του ενός αριθμοί με τα πρόσημά τους μέσα σε παρενθέσεις, μπροστά από τις οποίες μπορεί να υπάρχουν τα πρόσημα + ή -. Για να απαλείψουμε τις παρενθέσεις εργαζόμαστε ως εξής: |
- Όταν μια παρένθεση έχει μπροστά της το + (ή δεν έχει πρόσημο), μπορούμε να την απαλείψουμε μαζί με το + (αν έχει) και να γράψουμε τους όρους που περιέχει με τα πρόσημά τους.
|
(+5) + (-7) = +5 - 7 = -2
(9,1-6,2+3,4) + (-7,5+10-8,3) =
= 9,1-6,2 + 3,4-7,5 + 10-8,3 |
- Όταν μια παρένθεση έχει μπροστά της το -, μπορούμε να την απαλείψουμε μαζί με το - και να γράψουμε τους όρους που περιέχει με αντίθετα πρόσημα.
|
(-5) - (-7) = -5 + 7 = +2
-(9,1-6,2+3,4) - (-7,5+10-8,3) =
= -9,1+6,2-3,4+7,5-10+8,3 |
|
| |
| ΠΑΡΑΔΕΙΓΜΑΤΑ - ΕΦΑΡΜΟΓΕΣ |
 |
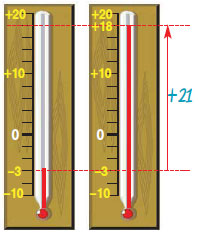
Ένα βράδυ το θερμόμετρο στο μπαλκόνι ενός σπιτιού έδειχνε -3° C και μέσα στο σπίτι 18°C. Πόση ήταν η διαφορά θερμοκρασίας; |
 |
|
 |
To πρόβλημα ζητάει να υπολογίσουμε τη διαφορά των θερμοκρασιών, δηλαδή τη διαφορά (+18) - (-3).
Αν παρατηρήσουμε το σχήμα θα δούμε ότι η διαφορά θερμοκρασίας μεταξύ του εσωτερικού του σπιτιού και του εξωτερικού του ήταν +21° C.
Σύμφωνα με τον ορισμό της αφαίρεσης ρητών θα έχουμε:
(+18) - (-3) = (+18) + (+3) = (+21) |
 |
Μικροπείραμα |
 |
Ένας έμπορος χρωστάει στον προμηθευτή του 897,56 € και του οφείλει ένας πελάτης 527,42 €. Πόσα € πρέπει να έχει στο ταμείο για να ξεχρεώσει; |
 |
|
| |
Αν x είναι το ποσό των χρημάτων που χρειάζεται, θα είναι:
x + (+527,42) = +897,56. Γνωρίζουμε ότι: x = (+897,56) - (+527,42).
Σύμφωνα με τον κανόνα της αφαίρεσης ρητών, έχουμε ότι:
x = (+897,56) + (-527,42). Άρα, x = +(897,56 - 527,42) ή x = +370,14 € |
 |
Να λυθούν οι εξισώσεις: (α) x + (+3) = (-9), (β) (-8) - x = +7 |
 |
|
| |
| (α) |
Αν είναι: x + (+3) = (-9) τότε x = (-9) - (+3) ή x = (-9) + (-3) ή x = (-12). Δηλαδή, x = -12. |
| (β) |
Εφ' όσον (-8) - x = +7 θα ισχύει ότι: (-8) = (+7) + x και επίσης: x = (-8) - (+7) ή x = (-8) + (-7) δηλαδή x = -15. |
|
 |
Να βρεθεί η τιμή της παράστασης: -13 - (0,38 - 11 - 13) + (0,38-11). |
 |
|
| |
| Έχουμε: |
-13 - (0,38 - 11 - 13) + (0,38 - 11) =
= -13 - 0,38 + 11 + 13 + 0,38 - 11 =
= -13 + 13 - 0,38 + 0,38 - 11 + 11 =
= 0 + 0 + 0 = 0 |
|
|
| |
| ΑΣΚΗΣΕΙΣ ΚΑΙ ΠΡΟΒΛΗΜΑΤΑ
Άσκηση 
|

|
| Τοποθέτησε ένα "x" στην αντίστοιχη θέση |
ΣΩΣΤΟ |
ΛΑΘΟΣ |
| (α) |
Στους ρητούς αριθμούς η αφαίρεση σημαίνει πάντα ελάττωση |
|
|
| (β) |
Αν η διαφορά δύο ρητών είναι αρνητικός αριθμός, τότε και οι δύο ρητοί είναι αρνητικοί αριθμοί. |
|
|
| (γ) |
Ισχύει στην αφαίρεση η αντιμεταθετική ιδιότητα: α - β = β - α |
|
|
| (δ) |
Ισχύει ότι: 6-(+8) + (+5) + (-3) + (2) + (-1) = 0 |
|
|
| (ε) |
Λύση της εξίσωσης x + (-3) = -2 είναι ο αριθμός +1 |
|
|
| (στ) |
Οι εξισώσεις x+ (-2) = +5 και x-( +7)=-Ί0+(+5) έχουν τηνίδια λύση. |
|
|
| (ζ) |
Λύση της εξίσωσης x - (-2) = -8 + (+7) - (-4) είναι ο αριθμός +1 |
|
|
|
 |
Υπολόγισε τις διαφορές:
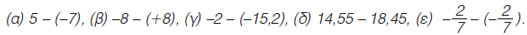
|
 |
Κάνε τις πράξεις:
(α |+3| +|-2| + |-9|, (β) |-20| + |-10| -|+ 10|, (γ) |-3| - |-2| + |-5| -|+6|. |
 |
Κάνε τις πράξεις:
(α) (+5) - (+3) + (+8), (β) (-25) + (-4) - (-10), (γ) (+12) + (+2) - (-8). |
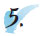 |
| Συμπλήρωσε τον πίνακα με τους κατάλληλους αριθμούς: |
| α |
β |
α+β |
α-β |
| +3 |
|
-5 |
|
| |
-8 |
+10 |
|
| -2 |
-5 |
|
|
| -9 |
|
+6 |
|
|
|
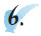 |
Να λύσεις τις εξισώσεις: (α) x+(-8)=-18, (β) x+12=-14, (γ) x+5/4=7/8, (δ) x-5/4=2 |
 |
| Συμπλήρωσε τις δύο τελευταίες στήλες του πίνακα: Τι συμπεραίνεις για τους αριθμούς των δύο αυτών στηλών; |
| α |
β |
α-β |
β-α |
| 7 |
3 |
|
|
| 2 $\dfrac{3}{4}$ |
3 $\dfrac{1}{4}$ |
|
|
| -5,55 |
-2,45 |
|
|
| 3 |
-2,1 |
|
|
|
|
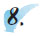 |
Υπολόγισε την τιμή των παραστάσεων με δύο τρόπους: (α) 11-(12-2) + (10-5)-(8+5),
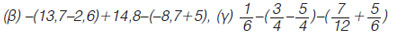
|
 |
| Συμπλήρωσε τον πίνακα: |
| x |
3,5 |
|
1,89 |
-$\dfrac{1}{4}$ |
| y |
-1,5 |
4,3 |
|
-$\dfrac{1}{4}$ |
| z |
|
-2,3 |
3,11 |
|
| x+y+z |
0 |
|
0,22 |
$\dfrac{1}{2}$ |
| x-y-z |
|
0 |
|
|
|
|
|
| |
|