Α.7.2. Απόλυτη τιμή ρητού - Αντίθετοι ρητοί

Μέρος Α' - Κεφάλαιο 7ο - Θετικοί και Αρνητικοί Αριθμοί

Α.7.2. Απόλυτη τιμή ρητού - Αντίθετοι ρητοί - Σύγκριση ρητών

ΔΡΑΣΤΗΡΙΟΤΗΤΑ 1η

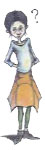Βρες πόσες μονάδες απέχουν από την αρχή Ο του άξονα τα σημεία Α, Β, Γ και Δ.

Εικόνα

Μικροπείραμα

ΔΡΑΣΤΗΡΙΟΤΗΤΑ 2η

Στην παρακάτω ευθεία βρες τις τετμημένες των σημείων Μ' και Μ.

Εικόνα

Τι παρατηρείς για τις τετμημένες των σημείων Μ' και Μ;
Προσπάθησε να τοποθετήσεις στην παραπάνω ευθεία των ρητών τα σημεία Α' και Α που απέχουν από την αρχή Ο του άξονα 3,5 μονάδες.
Κάνε το ίδιο για τα σημεία Β' και Β που απέχουν από την αρχή Ο του άξονα 6 μονάδες.

Μικροπείραμα

Θυμόμαστε - Μαθαίνουμε

Η απόλυτη τιμή ενός ρητού αριθμού α εκφράζει την απόσταση
του σημείου μετετμημένη α από την αρχή Ο του άξονα και συμβολίζεται με |α|.

Αντίθετοι ονομάζονται δύο αριθμοί που
είναι ετερόσημοι και έχουν την ίδια απόλυτη τιμή

Ο αντίθετος του x είναι ο -x.

Μικροπείραμα

H απόλυτη τιμή ενός θετικού αριθμού είναι ο ίδιος ο αριθμός.
H απόλυτη τιμή ενός αρνητικού αριθμού είναι ο αντίθετός του.
H απόλυτη τιμή του μηδενός είναι το μηδέν.

Δύο σημεία που βρίσκονται σε ίση απόσταση, δεξιά και αριστερά από την αρχή των αξόνων, έχουν τετμημένες, αντίθετους αριθμούς.

ΔΡΑΣΤΗΡΙΟΤΗΤΑ 3η

Μια κρύα μέρα του χειμώνα ο Κώστας κοιτούσε τη θερμοκρασία κάθε δύο ώρες. Οι ενδείξεις του θερμομέτρου, που έβλεπε, φαίνονται παρακάτω:

Εικόνα

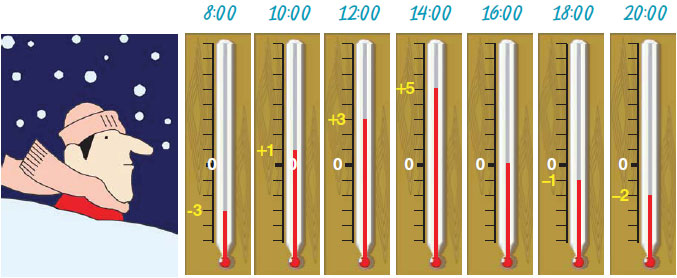
Μπορείς να καταγράψεις όλες τις ενδείξεις του θερμομέτρου με αύξουσα ή φθίνουσα σειρά;

Θυμόμαστε - Μαθαίνουμε

Ο μεγαλύτερος από δύο ρητούς αριθμούς είναι εκείνος που βρίσκεται δεξιότερα από τον άλλο πάνω στον άξονα.

Κάθε θετικός ρητός είναι μεγαλύτερος από κάθε αρνητικό ρητό αριθμό.

Το μηδέν είναι μικρότερο από κάθε θετικό αριθμό και μεγαλύτερο από κάθε αρνητικό αριθμό.
Ο μεγαλύτερος από δύο θετικούς ρητούς είναι εκείνος που έχει την μεγαλύτερη απόλυτη τιμή, δηλαδή αυτός που βρίσκεται δεξιότερα από τον άλλο πάνω στον άξονα.
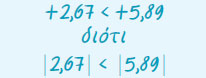Ο μεγαλύτερος από δύο αρνητικούς ρητούς είναι εκείνος που έχει την μικρότερη απόλυτη τιμή, δηλαδή αυτός που βρίσκεται δεξιότερα από τον άλλο πάνω στον άξονα.

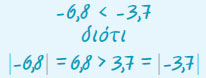ΠΑΡΑΔΕΙΓΜΑΤΑ - ΕΦΑΡΜΟΓΕΣ

Στον άξονα των αριθμών να τοποθετηθούν οι αριθμοί:

Εικόνα

Το σημείο Κ έχει τετμημένη -7. Να βρεθεί το σημείο Λ με αντίθετη τετμημένη.

Εικόνα

Πάνω σε άξονα x'Ox βρίσκουμε το σημείο K με τετμημένη -7. Τότε το Λ έχει τετμημένη τον αριθμό +7.

Εάν η απόλυτη τιμή του αριθμού α είναι 2, να βρεθεί ο αριθμός α.

Εφόσον \|α\|=2 τότε ο αριθμός α θα είναι, είτε το +2 είτε το -2, διότι \|+2\| = 2 και \|-2\| = 2 .
Παρατηρούμε ότι οι αριθμοί -2 και +2, έχουν την ίδια απόλυτη τιμή αλλά αντίθετο πρόσημο.

ΑΣΚΗΣΕΙΣ ΚΑΙ ΠΡΟΒΛΗΜΑΤΑ

Άσκηση Άσκηση

Εικόνα

Συμπλήρωσε τα παρακάτω κενά:
(α)	Η απόσταση του σημείου, με το οποίο αναπαριστάνεται ένας ρητός αριθμός, από την αρχή του άξονα λέγεται ......................................................... του αριθμού και είναι πάντα ......................................................... αριθμός.
(β)	Δύο ρητοί αριθμοί που έχουν την ίδια απόλυτη τιμή και είναι ετερόσημοι λέγονται .........................................................
(γ)	Αν ένας αριθμός α είναι θετικός ο αντίθετος του είναι ......................................................... Αν η απόλυτη τιμή ενός αριθμού είναι ίση με 6 τότε ο αριθμός είναι ο .............................. ή ο ..............................
(δ)	Από δύο θετικούς ρητούς μικρότερος είναι εκείνος που έχει την ......................................................... απόλυτη τιμή.
(ε)	Από δύο αρνητικούς ρητούς μεγαλύτερος είναι εκείνος που έχει την ......................................................... απόλυτη τιμή.

Να συμπληρώσεις τον πίνακα που ακολουθεί:

Αριθμός	-2,73	+7,66	-1,05	0	+8,07	-8
Απόσταση του σημείου που αντιστοιχεί από την αρχή του άξονα

Τοποθέτησε ένα "x" στην αντίστοιχη θέση		ΣΩΣΤΟ	ΛΑΘΟΣ
(α)	Iσχύει η ανισότητα: –5,7 < 5,7.
(β)	Ισχύει η ανισότητα: -7,6 > -6,7.
(γ)	Στην ανισότητα 2,3 < x < 4,7 ο x μπορεί να πάρει 2 ακέραιες τιμές.
(δ)	Υπάρχουν 5 ακριβώς ακέραιοι που αληθεύουν τη σχέση: -2≤x ≤+2
(ε)	Δύο ακέραιοι με αντίθετο πρόσημο είναι αντίθετοι.

Βρες την απόλυτη τιμή των ρητών: (α) +7,25, (β) -2,5, (γ) +16, (δ) -20,05, (ε) -58.

Βρες τους αριθμούς που έχουν ως απόλυτη τιμή: (α) 100, (β) 21,7, (γ) 0, (δ) 7,03, (ε) 5,2.

Συμπλήρωσε τον πίνακα:	Αριθμός	1		-19
	Αντίθετος				-8	12
	Απόλυτη τιμή		2				7

Τοποθέτησε στον άξονα x'Οx τα σημεία με τετμημένες:

-9, -5,5, +8, -3, -7,25, +1, +12, +3, +9. Ποια από αυτά είναι συμμετρικά ως προς την αρχή του άξονα;

Σχεδίασε τον άξονα x'Ox, με κατάλληλη μονάδα για να παραστήσεις τα σημεία με τετμημένες τους αριθμούς: -20,5, +15, -39,75, -68,25, +70, +52,25,+43, -69.

Να συγκρίνεις τους αριθμούς: (α) +41 και +38, (β) 9 και 11, (γ) -3 και -2, (δ) -9 και -16, (ε) 7 και -8, (στ) 0 και -3, (ζ) 0 και +4.

Να συγκρίνεις τους αριθμούς: (α) 11, -11 και |11|, (β) -3, +3 και |3|. Τι συμπεραίνεις;

Να γράψεις τους αριθμούς: -2, +7, +15, -3, 0, -4, +5, -8 και -10 σε αύξουσα σειρά.

Να συμπληρώσεις με το κατάλληλο σύμβολο: <, > ή = τα κενά, ώστε να προκύψουν αληθείς σχέσεις: (α) -3 ... -8,

(β) -4 ... 10, (γ) 0 ... -1, (δ) +3 ... 0, (ε) -5 ... -|-5|, (στ) -5 ... -(+5), (ζ) |+7| ...|-7|, (η) -(-8) ... -8, (θ) +3 ... -(+4), (ι) 0 ... -|-4|.

Το x παριστάνει έναν ακέραιο αριθμό. Για ποιες τιμές του x θα ισχύουν οι σχέσεις: (α) -13 < χ < -8, (β) -4 > χ > -5,
(γ) -2 < x < 5.