| Α.7.1. Θετικοί και Αρνητικοί Αριθμοί (Ρητοί αριθμοί) - H ευθεία των ρητών - Τετμημένη σημείου |
Οι αριθμοί που γνωρίσαμε, μέχρι τώρα, οι φυσικοί, οι δεκαδικοί και οι κλασματικοί, μπορούν να εκφράσουν τα φυσικά μεγέθη, όχι όμως και όλες τις ανθρώπινες δραστηριότητες και καταστάσεις. Άλλωστε, όταν τοποθετήσαμε τους φυσικούς αριθμούς πάνω σε μια ευθεία, πήραμε αυθαίρετα ένα σημείο ως αρχή και συνεχίσαμε "δεξιά", σε ίσες αποστάσεις, να γράφουμε τους γνωστούς μας αριθμούς. Κάθε "δεξιά" όμως μιας αρχής, προϋποθέτει και το "αριστερά". Όπως το δεξί χέρι προϋποθέτει το αριστερό του. Και ακόμα, δεν θα υπήρχε το "πάνω" χωρίς το "κάτω", το "ζεστό" χωρίς το "κρύο" κ.λπ. Έτσι, αν το πρώτο πούμε "θετικό" θα πρέπει να υπάρχει το αντίθετό του και να το πούμε "αρνητικό". Επίσης, σε κάθε στοιχείο του ενός χρειάζεται να αντιστοιχήσουμε ακριβώς ένα στοιχείο του άλλου και να βρούμε τρόπο να το συμβολίσουμε. Δε θα είναι δύσκολο, αφού είναι πράγματα που τα βιώνουμε καθημερινά. Όπως π.χ. η πρόβλεψη του καιρού στη δραστηριότητα που ακολουθεί. |
| |
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ 1η |
 |
 |
|
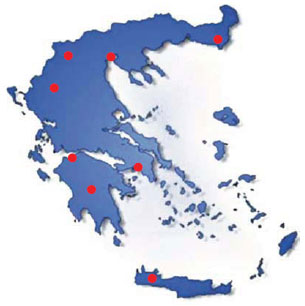
H μετεωρολογική υπηρεσία προέβλεψε ότι οι θερμοκρασίες στις διάφορες πόλεις θα είναι αυτές που αναγράφονται στον παρακάτω πίνακα:
| Αθήνα |
7° |
πάνω από το μηδέν |
| Θεσσαλονίκη |
3° |
κάτω από το μηδέν |
| Ιωάννινα |
5° |
κάτω από το μηδέν |
| Πάτρα |
2° |
πάνω από το μηδέν |
| Αλεξανδρούπολη |
8° |
κάτω από το μηδέν |
| Φλώρινα |
10° |
κάτω από το μηδέν |
| Τρίπολη |
6° |
κάτω από το μηδέν |
| Χανιά |
11° |
πάνω από το μηδέν |
|
| |
- Προσπάθησε να σημειώσεις στο χάρτη αριθμούς που να εκφράζουν τις συγκεκριμένες θερμοκρασίες.
|
Μικροπείραμα  |
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ 2η |
| |
Στον ανελκυστήρα ενός γκαράζ υπάρχουν τα κουμπιά που βλέπεις δίπλα.
- Τι εκφράζουν οι αριθμοί που είναι γραμμένοι στα κουμπιά;
|
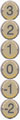 |
Μικροπείραμα  |
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ 3η |
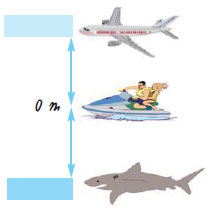 |
Στο διπλανό σχήμα παρατηρούμε ότι το αεροπλάνο πετάει στα 200 m και ο καρχαρίας βρίσκεται σε βάθος 200 m κάτω από την επιφάνεια της θάλασσας;
- Προσπάθησε να εκφράσεις με κατάλληλους αριθμούς τις θέσεις του αεροπλάνου και του καρχαρία σε σχέση με την επιφάνεια της θάλασσας;
| Σκεφτόμαστε |
Αν ο αριθμός 0 εκφράζει τη θέση της επιφάνειας της θάλασσας, τότε το αεροπλάνο πετάει στα +200 m και ο καρχαρίας βρίσκεται στα -200 m. |
|
|
|
Μετά από τα παραπάνω συμφωνούμε ότι: |
 |
Τα σύμβολα «+» και «-» λέγονται πρόσημα. Γράφονται πριν από τους αριθμούς και τους χαρακτηρίζουν, αντίστοιχα, ως θετικούς ή αρνητικούς. |
 |
Οι αριθμοί που συναντήσαμε μέχρι τώρα ήταν μόνο θετικοί και επομένως δεν υπήρχε ανάγκη να χρησιμοποιούμε πρόσημο. Η εισαγωγή των αρνητικών αριθμών δημιουργεί την ανάγκη της τοποθέτησης πρόσημου μπροστά από όλους τους αριθμούς. Έτσι γίνεται φανερό ποιοι αριθμοί είναι οι θετικοί και ποιοι οι αρνητικοί. |
 |
- Το μηδέν δεν είναι ούτε θετικός ούτε αρνητικός αριθμός
|
|
- Ομόσημοι λέγονται οι αριθμοί που έχουν το ίδιο πρόσημο.
|
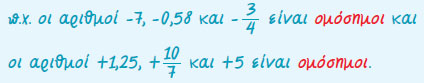 |
- Ετερόσημοι λέγονται οι αριθμοί που έχουν διαφορετικό πρόσημο
|
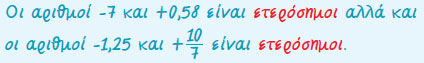 |
|
 |
|
|
Μικροπείραμα 
|
 |
Παράσταση των ρητών αριθμών με σημεία μιας ευθείας |
- Αν θεωρήσουμε αριστερά της αρχής Ο του ημιάξονα Οx των αριθμών, τον αντικείμενο αυτού ημιάξονα Ox', μπορούμε να παραστήσουμε τους αρνητικούς αριθμούς σε συμμετρικά σημεία, ως προς Ο, των αντιστοίχων σημείων που παριστάνουν τους θετικούς αριθμούς. Με τον ίδιο τρόπο μπορούμε να βρούμε σημεία που να παριστάνουν κλασματικούς ή δεκαδικούς αριθμούς.

- Ο άξονας x'Οx περιλαμβάνει όλους τους ρητούς αριθμούς (αρνητικούς, θετικούς και το μηδέν).
- Η θέση ενός σημείου Α επάνω στην ευθεία ορίζεται με έναν αριθμό που ονομάζεται τετμημένη του σημείου.

Το σημείο Α έχει τετμημένη 4 και το σημείο Β έχει τετμημένη -2. |
|
Μικροπείραμα  |
| ΠΑΡΑΔΕΙΓΜΑ - ΕΦΑΡΜΟΓΗ |
 |
|
Να εκφραστούν με τη βοήθεια των θετικών και αρνητικών ρητών αριθμών: (α) 13,75 m κάτω από την επιφάνεια της θάλασσας, (β) 20° Κέλσιου πάνω από το μηδέν, (γ) κέρδος 3.368,97 €, (δ) αύξηση κατά 2.527,15 €, (ε) μείωση κατά 50 μονάδες και (στ) έκπτωση 15% επί της τιμής. |
| |
 |
|
| |
|
(α) -13,75 m, (β) +20°, (γ) +3.368,07 €, (δ) +2.527,15 €, (ε) -50, (στ) -15% |
Μικροπείραμα  |
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ ΠΑ ΤΟ ΣΠΙΤΙ |
 |
|
Ας υποθέσουμε, ότι η στιγμή της γέννησής σου είναι το μηδέν, δηλαδή η αρχή της μέτρησης του χρόνου. Βρες μέχρι δέκα χρονολογίες, που αφορούν τα πιο σημαντικά, για σένα, προσωπικά και οικογενειακά γεγονότα και τοποθέτησέ τα στην παρακάτω ευθεία.

|
|
| |
| ΑΣΚΗΣΕΙΣ ΚΑΙ ΠΡΟΒΛΗΜΑΤΑ |

|
| Συμπλήρωσε τα παρακάτω κενά: |
| (α) |
Οι ρητοί που έχουν πρόσημο "+" λέγονται ..................................................................., ενώ αυτοί που
έχουν πρόσημο "-" λέγονται ................................................................... |
| (β) |
Οι αριθμοί με το ίδιο πρόσημο λέγονται ..................................................................., ενώ αυτοί με
διαφορετικό πρόσημο λέγονται ................................................................... |
| (γ) |
Στην ευθεία των αριθμών, δεξιά του μηδενός βρίσκονται οι ...................................................................
ρητοί και αριστερά του μηδενός οι ................................................................... ρητοί. |
|
 |
Να κατατάξεις τους παρακάτω αριθμούς σε δύο ομάδες, τους θετικούς και τους αρνητικούς: -3,1, +5, +8, -20, 7, -3, 18. |
 |
| Τοποθέτησε ένα "x" στην αντίστοιχη θέση |
ΣΩΣΤΟ |
ΛΑΘΟΣ |
| (α) |
Οι ακόλουθοι αριθμοί είναι όλοι θετικοί: +1, +5, +216, +3701 |
|
|
| (β) |
Οι αριθμοί που ακολουθούν είναι όλοι αρνητικοί: -3, -8, 7, -22 |
|
|
| |
Οι επόμενες τρεις ερωτήσεις αναφέρονται στο σχήμα που ακολουθεί. |
|
|
| |
 |
|
|
| (γ) |
H τετμημένη του σημείου Κ είναι +2 |
|
|
| (δ) |
Η τετμημένη του σημείου Λ είναι -4 |
|
|
| (ε) |
Tα σημεία Κ και Μ έχουν την ίδια τετμημένη |
|
|
|
 |
Στα ζεύγη αριθμών που ακολουθούν να βρεις ποιοι αριθμοί είναι ομόσημοι και ποιοι είναι ετερόσημοι: (α) 3 και +3, (β) 2 και 5, (γ) -2 και -4, (δ) 7 και +9, (ε) -2 και 1, (στ) 17 και -20, (ζ) -9 και -3,2, (η) -10,5 και 11, (θ) -3 και -100, (ι) +6,7 και +12,3. |
 |
Να εκφράσεις με ρητούς αριθμούς τις παρακάτω προτάσεις: (α) Κατάθεση 50.000 € (β) Ανάληψη 78.000 €, (γ) Αύξηση μισθού κατά 500 €, (δ) Μείωση επιτοκίου κατά 1 μονάδα, (ε) 30 μέτρα αριστερά. |
 |
Βρες τη λέξη που σχηματίζεται από τα γράμματα με τετμημένες -6, 10, 9, -9, 5, -5, 0 στο παρακάτω σχήμα. Στη συνέχεια γράψε μ' αυτό τον τρόπο ένα όνομα που σου αρέσει.

|
 |
Τα σημεία Α και Β έχουν τετμημένες α και β, αντίστοιχα. Να βρεθεί η τετμημένη του μέσου Μ του τμήματος ΑΒ όταν: (α) α = +5 και β = +8, (β) α = -4 και β = -13. |
|
|