Α.6.6. Αντιστρόφως ανάλογα ποσά |
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ 1η |
Ξεκινούν ταυτόχρονα από μια πόλη:
| (α) |
ένα αυτοκίνητο που τρέχει με ταχύτητα 120 Κm/h |
| (β) |
ένα αεροπλάνο με 600 Κm/h |
| (γ) |
μία μοτοσικλέτα με 75 Κm/h |
| (δ) |
ένα λεωφορείο που τρέχει με 80 Κm/h |
| (ε) |
ένα ελικόπτερο με 300 Κm/h |
| (στ) |
ένα ταξί με 100 Κm/h |
| (ζ) |
μία βέσπα με 60 Κm/h και |
| (η) |
ένα πούλμαν με 90 Κm/h |
To τέλος της διαδρομής είναι μια άλλη πόλη, που απέχει 600 Km.
- Βρες σε πόσες ώρες, θα φθάσει το καθένα στον προορισμό του και συμπλήρωσε τον παρακάτω πίνακα:
| Ταχύτητα σε Km/h |
|
|
|
|
|
|
|
|
| Χρόνος σε ώρες |
|
|
|
|
|
|
|
|
- Ποια σχέση συνδέει τα μεγέθη της ταχύτητας και του χρόνου;
- Τοποθέτησε τα ζεύγη των τιμών που βρήκες, σε ένα σύστημα ημιαξόνων και ένωσε τα σημεία, που ορίζουν τα ζεύγη αυτά, με μία γραμμή. Τι παρατηρείς;
Μικροπείραμα  |
 |
|
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ 2η |
Ένα συνεργείο που αποτελείται από 8 εργάτες χρειάζεται 30 ημέρες για να ολοκληρώσει ένα οικοδομικό έργο.
- Πόσες ημέρες θα χρειαστεί το
συνεργείο, που αποτελείται από
2, 4, 6, 10, 12, 24 ή 48 εργάτες για
να τελειώσει το ίδιο έργο;
- Μπορείς να συμπληρώσεις τον παρακάτω πίνακα;
|
 |
| |
Εργάτες συνεργείου |
2 |
4 |
6 |
8 |
10 |
12 |
24 |
48 |
| |
Ημέρες εργασίας |
|
|
|
30 |
|
|
|
|
|
- Τι παρατηρείς για το γινόμενο "εργάτες" · "ημέρες";
- Τοποθέτησε τα ζεύγη των τιμών του πίνακα, σε ένα σύστημα ημιαξόνων και ένωσε τα σημεία, που ορίζουν τα ζεύγη αυτά, με μία γραμμή. Τι παρατηρείς;
|
|
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ 3η |
Ένα ορθογώνιο παραλληλόγραμμο έχει διαστάσεις x και y. Αν γνωρίζεις ότι το εμβαδόν του ορθογωνίου είναι 144 m2, μπορείς να βρεις δεκατέσσερις ακέραιες τιμές των διαστάσεών του και να συμπληρώσεις τον παρακάτω πίνακα;
- Ποια σχέση συνδέει τις διαστάσεις του ορθογωνίου με το εμβαδόν του;
- Τοποθέτησε τα ζεύγη των τιμών του πίνακα, σε ένα σύστημα ημιαξόνων και ένωσε τα σημεία, που ορίζουν τα ζεύγη αυτά, με μία γραμμή. Τι παρατηρείς;
- Ποιο ορθογώνιο, απ' αυτά που βρήκες, έχει τη μικρότερη περίμετρο;
Μικροπείραμα  Μικροπείραμα Μικροπείραμα  |
|
| |
|
| |
| ΠΑΡΑΔΕΙΓΜΑ – ΕΦΑΡΜΟΓΗ |

|
Ένας ελαιοπαραγωγός χρησιμοποιεί δοχεία των 20 lt, 15 lt, 10 lt και 5 lt, για να συσκευάσει το λάδι που παράγει. Η παραγωγή του είναι 3.600 lt. Θέλει να συσκευάσει την ίδια ποσότητα λαδιού σε κάθε μία από τις τέσσερις διαφορετικές συσκευασίες.
| (α) |
Πόσα δοχεία χρειάζεται από κάθε είδος; |
| (β) |
Πόσο θα κοστίσει η συσκευασία της παραγωγής του αν στοιχίζει 0,4 € το δοχείο των 20 lt, 0,3 € το δοχείο των 15 lt, 0,2 € το δοχείο των 10 lt και 0,1 € το δοχείο των 5 lt; |
|
 |
|
| (α) |
Ο παραγωγός θέλει να συσκευάσει την ίδια ποσότητα λαδιού σε 4 διαφορετικά είδη δοχείων, άρα
σε κάθε είδος δοχείου θα συσκευάσει το 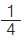 της
παραγωγής του, της
παραγωγής του,
δηλαδή 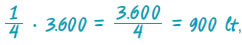 για κάθε είδος δοχείων. για κάθε είδος δοχείων.
Συνεπώς, θα ισχύει: x (Χωρητικότητα) ·y (Αριθμός Δοχείων) = 900 lt. Τότε, θα είναι:
| για x = 20 lt, είναι: |
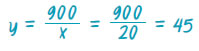 |
| για x = 15 lt, είναι: |
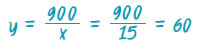 |
| για x = 10 lt, είναι: |
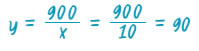 |
| για x = 5 lt, είναι: |
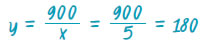 |
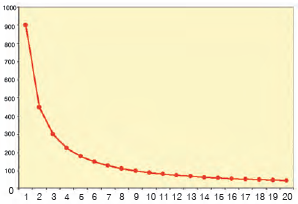
Έτσι, θα έχουμε τον παρακάτω πίνακα και το αντίστοιχο διάγραμμα.
| |
x (χωρητικότητα) |
20 |
15 |
10 |
5 |
| |
y (αριθμός δοχείων) |
45 |
60 |
90 |
180 |
|
 |
|
| (β) |
Τα ποσά Αριθμών δοχείων και Κόστος συσκευασίας είναι ανάλογα.
Έτσι σε κάθε είδος δοχείου θα έχουμε:
| Δοχεία 20 lt |
Αριθμός δοχείων |
1 |
45 |
Δηλαδή: |
ω = 45 · 0,4 |
άρα |
ω = 18 € |
| |
Κόστος δοχείων |
0,4 |
ω |
|
|
|
|
| Δοχεία 15 lt |
Αριθμός δοχείων |
1 |
60 |
Δηλαδή: |
ω = 60 · 0,3 |
άρα |
ω = 18 € |
| |
Κόστος δοχείων |
0,3 |
ω |
|
|
|
|
| Δοχεία 10 lt |
Αριθμός δοχείων |
1 |
90 |
Δηλαδή: |
ω = 90 · 0,2 |
άρα |
ω = 18 € |
| |
Κόστος δοχείων |
0,2 |
ω |
|
|
|
|
| Δοχεία 5 lt |
Αριθμός δοχείων |
1 |
180 |
Δηλαδή: |
ω = 180 · 0,1 |
άρα |
ω = 18 € |
| |
Κόστος δοχείων |
0,1 |
ω |
|
|
|
|
Έτσι, το συνολικό κόστος της συσκευασίας θα είναι το άθροισμα του κόστους των δοχείων και των τεσσάρων ειδών.
Συνολικό κόστος = 18 € + 18 € + 18 € +18 € = 72 €
Μικροπείραμα  |
|
|
| |
| ΑΣΚΗΣΕΙΣ ΚΑΙ ΠΡΟΒΛΗΜΑΤΑ |

|
Ποια από τα παρακάτω ποσά είναι αντιστρόφως ανάλογα; |
|
|
(Τοποθέτησε ένα "x" στην αντίστοιχη θέση) |
ΣΩΣΤΟ |
ΛΑΘΟΣ |
| (α) |
Η βάση και το εμβαδόν ενός τριγώνου, με σταθερό ύψος. |
|
|
| (β) |
Η παροχή μιας βρύσης και ο χρόνος που χρειάζεται για να γεμίσει μια μπανιέρα |
|
|
| (γ) |
Το εμβαδόν της ρωγμής ενός πλοίου και ο χρόνος που απαιτείται, για να γεμίσουν τα αμπάρια του με νερό. |
|
|
| |
|
| (δ) |
Ο αριθμός ατόμων και το βάρος του παγωτού που θα φάνε, από ένα οικογενειακό παγωτό 2 Κg. |
|
|
| |
|
| (ε) |
Η χωρητικότητα των μπουκαλιών και ο αριθμός μπουκαλιών που χρειαζόμαστε, για να εμφιαλώσουμε 100 lt κρασιού. |
|
|
| |
|
| (στ) |
Ο αριθμός των ατόμων και οι σκηνές των 2 ατόμων που χρειάζονται, για να κατασκηνώσουν. |
|
|
|
 |
Συμπλήρωσε τα παρακάτω κενά:
| (α) |
Δύο ποσά είναι αντιστρόφως ανάλογα και η τιμή του ενός διπλασιάζεται, τότε η αντίστοιχη τιμή του άλλου …………………………………. |
| (β) |
Η γραφική αναπαράσταση δύο αντιστρόφως ανάλογων ποσών είναι ………………….. γραμμή και ονομάζεται ………………………………….. |
|
 |
| (α) |
| x |
1 |
2 |
3 |
4 |
| y |
2 |
1 |
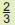 |
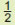 |
|
(β) |
| x |
0,25 |
0,4 |
0,5 |
| y |
10 |
6,25 |
5 |
|
| |
| (γ) |
| x |
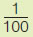 |
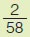 |
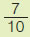 |
4 |
| y |
100 |
29 |
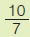 |
$\dfrac{1}{4}$ |
|
(δ) |
|
Ποιοι από αυτούς είναι πίνακες τιμών αντιστρόφως ανάλογων ποσών; |
 |
Τα ποσά x και y είναι αντιστρόφως ανάλογα.
| (α) |
Συμπλήρωσε τον πίνακα :
| |
x |
0,2 |
0,5 |
0,7 |
1 |
|
|
2,3 |
3 |
|
10 |
12 |
| |
y |
|
|
|
3,5 |
2,5 |
1,75 |
|
|
0,875 |
|
|
|
| (β) |
Βρες τα σημεία που παριστάνουν κάθε ζευγάρι τιμών (x, y), σε κατάλληλο σύστημα ορθογωνίων ημιαξόνων και σχεδίασε την υπερβολή. |
Μικροπείραμα  |
 |
Για την αναδάσωση μιας πλαγιάς, εργάστηκαν 20 εργάτες για 10 ημέρες. Πόσοι εργάτες, ίδιας απόδοσης, χρειάζονται για να αναδασώσουν την έκταση αυτή, σε 8 ημέρες; |
 |
Σε ένα αγρόκτημα, τοποθέτησαν ντομάτες σε 50 καφάσια, των 12 Κg το καθένα. Πόσα καφάσια των 20 Kg θα χρειαζόντουσαν για να τοποθετήσουν τις ντομάτες. Αν κάθε καφάσι των 12 Kg στοιχίζει 0,28 € και κάθε καφάσι των 20 Kg 0,46 €, ποια συσκευασία τους συμφέρει, ώστε να ελαχιστοποιηθεί το κόστος συσκευασίας του προϊόντος τους; |
 |
Το πετρέλαιο που υπάρχει στη δεξαμενή μιας πολυκατοικίας, επαρκεί για 30 ημέρες, όταν καταναλώνονται 80 lt την ημέρα. Όταν το κρύο δυναμώνει, η ημερήσια κατανάλωση αυξάνεται, κατά 20%. Για πόσες ημέρες θα φτάσει το πετρέλαιο; |
|
|