Α.6.2. Λόγος δύο αριθμών – Αναλογία |
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ 1η |
 |
Έχουμε τα παρακάτω τρία τετράγωνα:
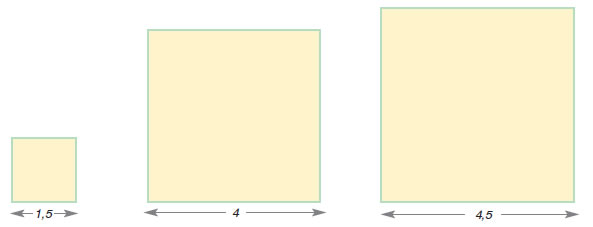
- Συμπλήρωσε τον παρακάτω πίνακα:
| Πλευρά τετραγώνου |
1,5 cm |
4 cm |
4,5 cm |
| Περίμετρος τετραγώνου |
|
|
|
- Εξήγησε πώς προκύπτουν οι αριθμοί της δεύτερης σειράς.
- Βρες για κάθε τετράγωνο το κλάσμα πλευρά προς περίμετρο.
- Ποιο είναι το συμπέρασμα που βγάζεις;
Μικροπείραμα  |
|
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ 2η |
Χρησιμοποιούμε τη φωτογραφική μηχανή για να απεικονίσουμε εικόνες αντικειμένων. Οι εικόνες αυτές δείχνουν τα πραγματικά αντικείμενα σε σμίκρυνση. Στη φωτογραφία το ύψος ενός παιδιού είναι 2 cm ενώ γνωρίζουμε ότι το πραγματικό του ύψος είναι 1,65 m = 165 cm.
- Πόση θα είναι τότε η σμίκρυνσή του στη φωτογραφία;
|
 |
|
|
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ 3η |
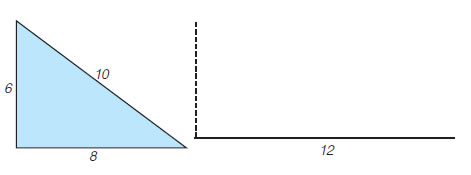
Σχεδίασε το τρίγωνο του παρακάτω σχήματος και μετά σχεδίασέ το μεγεθυσμένο, ώστε η πλευρά μήκους 8 cm να έχει νέο μήκος 12 cm.
|
 |
Μικροπείραμα  |
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ 4η |
|
| |
|
 |
- Το πηλίκο δύο αριθμών λέγεται και λόγος των αριθμών αυτών.
- Η ισότητα λόγων ονομάζεται αναλογία.
- Ο λόγος της απόστασης δύο σημείων μιας εικόνας ενός αντικειμένου προς την
απόσταση των δύο αντίστοιχων σημείων του ιδίου αντικειμένου, εφόσον οι
απόστάσεις μετριούνται με την ίδια μονάδα, ονομάζεται κλίμακα.
- Δύο σχήματα λέγονται όμοια όταν το ένα αποτελεί σμίκρυνση ή μεγέθυνση του άλλου (π.χ. στην παραπάνω δραστηριότητα το ΑΒΓΔ είναι μεγέθυνση του ΕΖΘΗ με λόγο 2:1).
- Αν οι λόγοι των αντιστοίχων πλευρών δύο παραλληλογράμμων είναι ίσοι,
τότε αυτοί θα είναι ίσοι και με τον λόγο των περιμέτρων τους.
- Κάθε σχέση αναλογίας
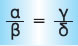 είναι ισοδύναμη με τη σχέση είναι ισοδύναμη με τη σχέση 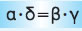
|
|
|
| |
| ΠΑΡΑΔΕΙΓΜΑ - ΕΦΑΡΜΟΓΗ |
|
Μετρούμε μια απόσταση, σε χάρτη, με κλίμακα 1:10.000.000 και τη βρίσκουμε ίση με 2,4 cm. Ποια είναι η πραγματική απόσταση των δύο σημείων; |
 |
 |
|
| |
Αφού δίνεται η κλίμακα 1:10.000.000, στο 1 cm του χάρτη αντιστοιχούν 10.000.000 cm στην πραγματικότητα.
Συνεπώς, αν τα 2,4 cm του χάρτη αντιστοιχούν σε x cm στην πραγματικότητα
θα έχουμε: 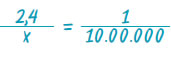 . Επομένως ισχύει ότι: . Επομένως ισχύει ότι:
1 ·x = 2,4 · 10.000.000 ή x = 24.000.000 cm = 240.000 m = 240 Km. |
|
| |
| ΑΣΚΗΣΕΙΣ ΚΑΙ ΠΡΟΒΛΗΜΑΤΑ |

|
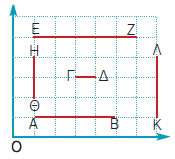
Να βρεις τους λόγους των διαφόρων ευθύγραμμων τμημάτων που είναι στο σχέδιο.
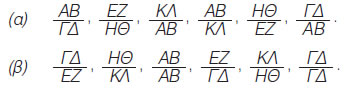
|
 |
|
 |
|
 |
Σε μια φωτογραφία το ύψος ενός ανθρώπου είναι 4 cm, ενώ το πραγματικό το ύψος είναι 1,76 m. Πόσο έχουν σμικρυνθεί όλα τα αντικείμενα της φωτογραφίας;
Μικροπείραμα  |
 |
|
 |
Ένας προβολέας διαφανειών προβάλλει το κείμενο μιας διαφάνειας στον απέναντι τοίχο. Αν ένα "Α" έχει ύψος 7 mm στη διαφάνεια και 4,2 cm στον τοίχο, ποια είναι η μεγέθυνση που δίνει ο προβολέας; |
 |
Η σύνθεση μιας μπλούζας είναι 80% βαμβάκι και το υπόλοιπο πολυεστέρας. Αν η μπλούζα ζυγίζει 820 gr, πόσα γραμμάρια ζυγίζουν τα νήματα του πολυεστέρα που περιέχει; |
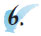 |
| Να συμπληρώσεις τον πίνακα: |
| Κλίμακα |
1 : 5 |
3 : 8 |
1 : 30 |
|
1 : 100 |
| Μήκος σε σχέδιο |
4 cm |
|
12 cm |
2 cm |
3,5 cm |
| Πραγματικό μήκος |
|
24 cm |
|
10 cm |
|
|
|
 |
Οι διαστάσεις ενός ορθογωνίου παραλληλογράμμου είναι x + 2 και x. |
| (α) |
Να γράψεις τη σχέση που συνδέει την περίμετρο Π του ορθογωνίου με το x. |
| (β) |
Να συμπληρώσεις τον πίνακα: |
|
|
|
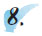 |
Αν οι διαστάσεις ενός δωματίου, σε ένα σχέδιο με κλίμακα 1 : 250, είναι 3 x 5, οι πραγματικές διαστάσεις του δωματίου θα είναι ….. x …. . |
 |
| Αν ανακατέψουμε 2 κιλά κόκκινο χρώμα και 3 κιλά κίτρινο χρώμα, φτιάχνουμε μια συγκεκριμένη απόχρωση του πορτοκαλί. Αν ανακατέψεις 5 κιλά κόκκινο χρώμα και 6 κιλά κίτρινο, θα πάρεις την ίδια απόχρωση; Δικαιολόγησε την απάντησή σου. |
 |
|
|
| |
| ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ ΓΙΑ ΤΟ ΣΠΙΤΙ |
|
| ΙΣΤΟΡΙΚΗ ΑΝΑΔΡΟΜΗ |
| Οι μαθηματικές έννοιες διαμορφώθηκαν και εξελίχτηκαν παράλληλα με την ανθρώπινη σκέψη. Φυσικά μεγέθη, όπως το βάρος, το μήκος, η επιφάνεια και ο όγκος, έδιναν αφορμές για μέτρηση και για σύγκριση, δηλαδή για λόγους και αναλογίες. Η συστηματική, όμως, μελέτη των εννοιών αυτών άρχισε στην αρχαία Ελλάδα τον 6ο π.Χ. αιώνα. |
 |
Ο Πυθαγόρας, που έζησε από το 580 π.Χ. μέχρι πιθανόν το 490 π.Χ., ήταν από τους πρώτους Έλληνες που ασχολήθηκε με τους λόγους και τις αναλογίες των φυσικών αριθμών. Υπάρχει μια παράδοση που αναφέρει τον τρόπο με τον οποίο ο Πυθαγόρας οδηγήθηκε σε αυτήν την έρευνα. Στην Αλεξάνδρεια, όπου έζησε αρκετά χρόνια, βρέθηκε μια μέρα κοντά σε κάποιο σιδηρουργείο όπου τέσσερις τεχνίτες κτυπούσαν με τα σφυριά τους ένα πυρακτωμένο μέταλλο. Ο ήχος από τα κτυπήματα ήταν παράξενα μελωδικός. Αυτό κέντρισε την περιέργεια του Πυθαγόρα, που αναζήτησε το λόγο της απροσδόκητης μελωδίας αυτών των ήχων.
Πυθαγόρας  |
Ζήτησε από τους τεχνίτες να εξετάσει τα σφυριά τους. Παρατήρησε ότι το βάρος τους δεν ήταν το ίδιο. Συγκρίνοντας το πιο βαρύ με τα υπόλοιπα, βρήκε τους λόγους 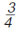 , , 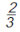 και και 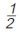 αντίστοιχα. Σκέφτηκε ότι οι λόγοι αυτοί, πιθανόν, να είχαν κάποια σχέση με τους ήχους που άκουσε. Πήρε τότε τέσσερις μεταλλικές χορδές και τις τέντωσε έτσι, ώστε τα μήκη τους να έχουν αντίστοιχους λόγους. Δηλαδή, η δεύτερη είχε μήκος ίσο με τα αντίστοιχα. Σκέφτηκε ότι οι λόγοι αυτοί, πιθανόν, να είχαν κάποια σχέση με τους ήχους που άκουσε. Πήρε τότε τέσσερις μεταλλικές χορδές και τις τέντωσε έτσι, ώστε τα μήκη τους να έχουν αντίστοιχους λόγους. Δηλαδή, η δεύτερη είχε μήκος ίσο με τα 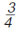 του μήκους της πρώτης. Η τρίτη του μήκους της πρώτης. Η τρίτη 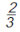 και η τέταρτη είχε μήκος ίσο με το και η τέταρτη είχε μήκος ίσο με το 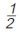 της πρώτης. της πρώτης. |
| Έκρουσε τις χορδές και διαπίστωσε ότι οι ήχοι είχαν την ίδια μελωδική σχέση με αυτήν που άκουσε στο σιδηρουργείο. Ήταν μια "αρμονία" ήχων (συγχορδία). Με τον τρόπο αυτό, ο Πυθαγόρας ανακάλυψε αρμονικούς τόνους της μουσικής κλίμακας. |
| Έτσι, οι λόγοι των φυσικών αριθμών ερμήνευαν φαινόμενα που κανείς μέχρι τότε δεν μπόρεσε να συσχετίσει και να εξηγήσει. Ο δρόμος για την αναζήτηση της γνώσης είχε ανοίξει. Η έρευνα και η ερμηνεία των φαινομένων της φύσης είχε ήδη διαμορφώσει στο νου των ανθρώπων ένα νέο κώδικα, μια νέα "παγκόσμια" γλώσσα: τα μαθηματικά. |
|
| ΣΧΕΔΙΟ ΕΡΓΑΣΙΑΣ |
| Στο σχήμα βλέπεις τρεις διαφορετικούς τρόπους, με τους οποίους το σημείο Μ χωρίζει ένα ευθύγραμμο τμήμα ΑΒ, ορίζοντας τις αντίστοιχες αναλογίες, ανάμεσα στα μέρη του. |
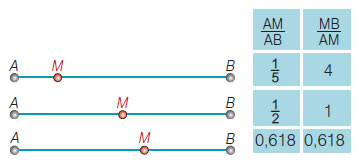 |
|
 |
Οι αρχαίοι Έλληνες είχαν επιλέξει τον τρίτο τρόπο ως καλύτερο αισθητικά και κατασκεύαζαν όλα τα μνημεία τους χρησιμοποιώντας αυτή τη συγκεκριμένη αναλογία στις διαστάσεις τους, όπως π.χ. μεταξύ των δύο
διαστάσεων της βάσης του ναού του Παρθενώνα της
Ακρόπολης των Αθηνών. Η αναλογία αυτή ονομάστηκε "χρυσή τομή".
Χρυσή τομή  |
 |
|
Αλλά και η φύση φαίνεται ότι έχει
παρόμοιες προτιμήσεις!
Την αναλογία της "χρυσής τομής"
βρίσκουμε ανάμεσα στα μήκη των
μελών του ανθρώπινου σώματος,
αλλά και στις διαστάσεις των σχημάτων πολλών φυτών και ζώων. |
 |
|
-
Υπάρχει τέτοια αναλογία στα διάφορα αντικείμενα που παρατηρούμε
γύρω μας.
-
Προσπάθησε να βρεις την αναλογία της "χρυσής τομής" σε:
(α) μνημεία, (β) ζωγραφικούς πίνακες, (γ) ανθρώπινες κατασκευές, (δ) σχήματα ζώων και φυτών, (ε) ανθρώπινο σώμα και άλλα.
-
Συνδέεται η επιλογή της "χρυσής τομής" από τους ανθρώπους στη συγκεκριμένη εποχή με επιστημονικά, αισθητικά, κοινωνικά, θρησκευτικά, οικονομικά, πολιτιστικά κ.λπ. αίτια; Εάν ναι προσπάθησε να δικαιολογήσεις την απάντησή σου.
-
Προσπάθησε να αποτυπώσεις, με τη βοήθεια ίσως και του υπολογιστή, σχέδια των μορφών ή των σχημάτων που έχουν την αναλογία της "χρυσής τομής".
Μικροπείραμα  |
|
|