Α.4.3. Παραδείγματα επίλυσης προβλημάτων |
| |
| ΠΑΡΑΔΕΙΓΜΑΤΑ - ΕΦΑΡΜΟΓΕΣ |
|
Η Χριστίνα ξόδεψε τα μισά της χρήματα για να αγοράσει 2 τετράδια και μαρκαδόρους. Αν είναι γνωστό, ότι κάθε τετράδιο στοιχίζει 1 € και όλοι οι μαρκαδόροι 3 €, ποιο είναι το ποσό των χρημάτων που είχε η Χριστίνα πριν από τις αγορές αυτές; |

|

|
Το ζητούμενο του προβλήματος είναι το ποσό των
χρημάτων που είχε η Χριστίνα, δηλαδή ο άγνωστος x του προβλήματος.
Το πρόβλημα μπορεί να
περιγραφεί απλούστερα με την εξίσωση:
«τα χρήματα που ξοδεύτηκαν» = «τα χρήματα που
κόστιζαν οι αγορές»
ή «τα μισά χρήματα της Χριστίνας»
= «το κόστος των τετραδίων»
+ «το κόστος μαρκαδόρων»
| ή |
x : 2 |
= 2 · 1 + 3 |
| ή |
x : 2 |
= 2 + 3 |
| ή |
x : 2 |
= 5 |
| ή |
x |
= 5 · 2 |
| ή |
x |
= 10 |
Επαλήθευση:
Τα μισά των 10 € είναι 5 € και τα έξοδα είναι 2 · 1 € + 3 € = 5 €. |
 |
Η δεξαμενή της κοινότητας χωράει 3.000 m3 νερό. Κάθε μέρα ξοδεύονται 300 m3 από τα νοικοκυριά και
άλλα 200 m3 από τις βιοτεχνίες. Για τη συντήρηση του δικτύου, σταμάτησε η παροχή νερού προς τη δεξαμενή. Τέσσερις ημέρες μετά την έναρξη των εργασιών αποφασίζεται να ξοδεύονται μόνο 400 m3 συνολικά κάθε ημέρα. Πόσες ημέρες ακόμη πρέπει να κρατήσουν τα έργα συντήρησης, ώστε να μη μείνουν χωρίς νερό οι κάτοικοι της κοινότητας; |
 |
|
| |
Το ζητούμενο του προβλήματος είναι το επιπλέον πλήθος των ημερών συντήρησης του δικτύου, δηλαδή ο άγνωστος x του προβλήματος.
Το πρόβλημα μπορεί να περιγραφεί με την εξίσωση:
"ποσό νερού που καταναλώνεται"= "ποσό νερού
δεξαμενής"
ή αναλυτικότερα
"ποσό νερού που καταναλώνεται στις τέσσερις ημέρες της συντήρησης" + "ποσό νερού που καταναλώνεται στις επιπλέον ημέρες συντήρησης"
= "ποσό νερού δεξαμενής"
| ή |
(300 + 200) |
· 4 |
+ 400 · |
x = 3.000 |
| ή |
500 |
· 4 |
+ 400 · |
x = 3.000 |
| ή |
2.000 |
|
+ 400 · |
x = 3.000 |
| ή |
|
|
400 · |
x = 3.000 – 2.000 |
| ή |
|
|
400 · |
x = 1.000 |
| ή |
|
|
|
x = 1.000 : 400 |
| ή |
|
|
|
x = 2,5 ημέρες |
|
Επαλήθευση: 2,5 · 400 + 4 · (200 + 300) = 3.000 ή 1.000 + 2.000 = 3.000 ή 3.000 = 3.000
|
 |
Ένας εργάτης για μια εργασία πέντε ημερών συμφώνησε να πάρει προκαταβολή το
μισό της αμοιβής του και το υπόλοιπο αυτής να το πληρωθεί όταν τελειώσει η εργασία.
Αν η προκαταβολή ήταν 180€, ποιό ήταν το μεροκάματό του; |
 |
|
| |
Έστω ότι είναι x το μεροκάματο του εργάτη. Τότε η αμοιβή του εργάτη για την πενθήμερη εργασία θα είναι 5 · x και το μισό αυτής θα είναι $\dfrac{5 \cdot x}{2}$. Συνεπώς η εξίσωση που περιγράφει το πρόβλημα θα είναι:
$\dfrac{5 \cdot x}{2}$=180 ή $\dfrac{5}{2} \cdot x = 180$ ή χ=180:$\dfrac{5}{2}$ ή χ=180 $\cdot\dfrac{2}{5}$ ή χ=$\dfrac{360 }{5}$ ή χ=72€ |
Μικροπείραμα  Μικροπείραμα Μικροπείραμα  |
|
 |
| Μετά τη συνεδρίαση και τα 10
μέλη του διοικητικού συμβουλίου
μιας εταιρείας ανταλλάσσουν
μεταξύ τους χειραψίες. Πόσες
χειραψίες γίνονται συνολικά; |
 |
|
 |
| |
| 1ος τρόπος: |
Αν υποθέσουμε ότι φεύγει ένας - ένας και χαιρετάει τους υπόλοιπους θα έχουμε ότι:
Ο πρώτος θα ανταλλάξει, συνολικά, 9 χειραψίες. Ο δεύτερος 8, ο τρίτος 7, ο τέταρτος 6, ο πέμπτος 5, ο έκτος 4, ο έβδομος 3, ο όγδοος 2, ο ένατος 1 και δέκατος καμία.
Επομένως, ο συνολικός αριθμός θα είναι: |
| 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 9) + (2 + 8) + (3 + 7) + (4 + 6) + 5 = 10 + 10 + 10 + 10 + 5 = 45 |
| |
Άρα, η λύση είναι ότι θα γίνουν συνολικά 45 χειραψίες. |
| 2ος τρόπος: |
Γνωρίζουμε ότι ο καθένας κάνει χειραψία με τους υπόλοιπους.
Επομένως, αφού όλοι είναι 10, ο καθένας θα κάνει 10 – 1 = 9 χειραψίες.
Άρα συνολικά θα γίνουν 10 φορές επί 9, δηλαδή 10 · 9 = 90 χειραψίες.
Όμως, μεταξύ δύο ανθρώπων η χειραψία είναι μία και εμείς τη μετρήσαμε διπλή (μία για καθένα από τους δύο).
Επομένως, αυτές που έγιναν συνολικά θα είναι οι μισές, δηλαδή
90 : 2 = 45.
Μικροπείραμα 
 |
|
|
| |
| ΑΣΚΗΣΕΙΣ ΚΑΙ ΠΡΟΒΛΗΜΑΤΑ |
|
Η διαφορά της ηλικίας της κόρης από τη μητέρα της είναι 25 χρόνια.
Αν η κόρη είναι 18 ετών, πόσων ετών είναι η μητέρα; |
 |
 |
Πόσοι μαθητές είναι τα 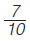 των μαθητών ενός σχολείου, αν τα των μαθητών ενός σχολείου, αν τα 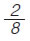 των μαθητών, αυτού του σχολείου, είναι 60 μαθητές; των μαθητών, αυτού του σχολείου, είναι 60 μαθητές;
Μικροπείραμα  |
 |
Να βρεις τρεις διαδοχικούς φυσικούς αριθμούς που έχουν άθροισμα 1533.
Μικροπείραμα  |
 |
Βρες το ψηφίο που λείπει από τον αριθμό 75  3, ώστε αυτός να διαιρείται με το 9. 3, ώστε αυτός να διαιρείται με το 9. |
 |
Σε ένα διαγώνισμα, κάθε μαθητής πρέπει να απαντήσει σε 100 ερωτήσεις. Θα πάρει 3 μονάδες, για κάθε σωστή απάντηση και μόνο 1 μονάδα, για κάθε λανθασμένη. Ένας μαθητής πήρε συνολικά 220 μονάδες. Σε πόσες ερωτήσεις απάντησε σωστά; |
 |
Η ηλικία ενός πατέρα είναι τετραπλάσια από την ηλικία του γιου του. Οι δύο ηλικίες
μαζί συμπληρώνουν μισό αιώνα. Πόσο χρονών είναι ο καθένας; |
 |
Τρία αδέλφια μοιράζονται, εξίσου, μια κληρονομιά, που είναι ένα χωράφι και ένα διαμέρισμα. Ο πρώτος παίρνει το χωράφι. Ο δεύτερος παίρνει το διαμέρισμα, αλλά δίνει στον πρώτο 600 € και στον τρίτο 15.000 €. Ποια ήταν η αξία του χωραφιού και ποια του διαμερίσματος; |
 |
| Σε κάθε μια από τις πράξεις (α) και (β) τα γράμματα αντιστοιχούν σε διαφορετικά μεταξύ τους ψηφία. Αντικατέστησε τα γράμματα Α, Β, Γ και Δ με τα κατάλληλα ψηφία. |
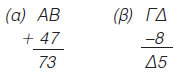 |
|
 |
Από μία ποσότητα κρασιού, αφαιρούμε 18 lt. Η υπόλοιπη ποσότητα χωράει σε δοχεία
των 7 lt. Αν γνωρίζεις ότι η αρχική ποσότητα είναι μικρότερη από 100 lt και μεγαλύτερη
από 90 lt, πόσα lt είναι η ποσότητα αυτή; Πόσα δοχεία θα χρησιμοποιήσουμε; |
 |
Ένας παραγωγός έφτιαξε 100 lt ξύδι και θέλει να το συσκευάσει σε μπουκάλια που χωράνε 0,75 lt. Να βρεις: (α) Πόσα μπουκάλια θα χρειαστεί, (β) Πόσα lt θα του περισσέψουν. |
 |
Δύο συνεργεία καθαρισμού ακτών καθαρίζουν μία μεγάλη παραλία μήκους 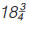 Κm. Το πρώτο συνεργείο καθαρίζει Κm. Το πρώτο συνεργείο καθαρίζει 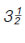 Κm και το δεύτερο συνεργείο Κm και το δεύτερο συνεργείο 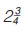 Κm, κάθε μέρα. Τα δύο συνεργεία εργάζονται, στα δύο άκρα της παραλίας, έως ότου συναντηθούν. Σε πόσες ημέρες θα έχουν ολοκληρώσει τον καθαρισμό της παραλίας; Κm, κάθε μέρα. Τα δύο συνεργεία εργάζονται, στα δύο άκρα της παραλίας, έως ότου συναντηθούν. Σε πόσες ημέρες θα έχουν ολοκληρώσει τον καθαρισμό της παραλίας; |
 |
Ένα κατάστημα προσφέρει τους υπολογιστές με έκπτωση 20%. Ο Γιώργος πήγε με
τον πατέρα του και αγόρασε έναν υπολογιστή και ένα κινητό τηλέφωνο αξίας 230 € και
πλήρωσαν συνολικά 1.070€. Ποια ήταν η αρχική αξία του υπολογιστή;
|
 |
Αυτή τη χρονιά η ηλικία ενός ανθρώπου είναι πολλαπλάσιο του 7 και την επόμενη χρονιά είναι πολλαπλάσιο του 9. Αν γνωρίζουμε ότι δεν είναι αιωνόβιος, ποια είναι η ηλικία του; |
|
|