| Α.3.5. Μονάδες μέτρησης |
| Η φιλοδοξία δεν είναι εύκολο να μετρηθεί. Ούτε ο φόβος. Υπάρχουν όμως πράγματα που μπορούν να μετρηθούν, όπως π.χ. το μήκος, το βάρος, ο χρόνος. Για να τα μετρήσουμε χρειαζόμαστε για το καθένα μια μονάδα μέτρησης. Αλλά και αυτό δεν φτάνει, διότι δεν είναι όλα τα μεγέθη ακέραια πολλαπλάσια της μονάδας. Θα πρέπει, λοιπόν, να δημιουργήσουμε και υποδιαιρέσεις της μονάδας. Έτσι θα είμαστε πιο ακριβείς στις μετρήσεις μας. Ας προχωρήσουμε τώρα με μια δραστηριότητα που μετράει τις δραστηριότητες του Γιάννη που δεν πέρασε καθόλου άσχημα το πρωί της Κυριακής. |
| |
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ 1η |
 |
Ο Γιάννης ξύπνησε την Κυριακή το πρωί, στις οκτώ και τέταρτο και ως τις έντεκα και μισή έπαιζε. Από τις έντεκα και μισή, ως τις δώδεκα, είδε τηλεόραση.
- Πόσο χρόνο πέρασε σε
κάθε δραστηριότητά του;
α) Με μονάδα μέτρησης
την ώρα;
β) Με μονάδα μέτρησης το τέταρτο;
γ) Με μονάδα μέτρησης το πεντάλεπτο;
δ) Με μονάδα μέτρησης το λεπτό;
ε) Με μονάδα μέτρησης το δευτερόλεπτο;
- Τι παρατηρείς; Πώς σχετίζονται μεταξύ
τους οι μετρήσεις του κάθε χρονικού
διαστήματος με διαφορετικές μονάδες
μέτρησης του χρόνου;
|
 |
|
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ 2η |
| |
Η μάζα του κυπέλλου του σχήματος να μετρηθεί με μονάδα μέτρησης τα 50 g, τα 100 g, τα 500 g και το 1 Κg.
|
 |
|
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ 3η |
 |
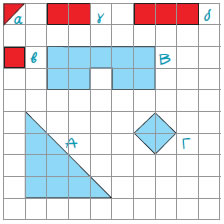
Προσπάθησε να μετρήσεις στην επόμενη σελίδα τα Α, Β και Γ, με βάση τις τέσσερις διαφορετικές μονάδες μέτρησης α, β, γ και δ.
Από τη μέτρηση θα έχουμε τα παρακάτω αποτελέσματα:
| Α = 16 α, |
Α = 8 β, |
Α = 4 γ, |
Α = 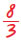 δ δ |
| Β = 18 α, |
Β = 9 β, |
Β = 4,5 γ, |
Β = 3 δ |
| Γ = 4 α, |
Γ = 2 β, |
Γ = 1 γ, |
Γ = 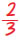 δ δ |
Παρατηρούμε ότι ο αριθμός που εκφράζει το εμβαδόν μιας επίπεδης επιφάνειας εξαρτάται από τη μονάδα μέτρησης που χρησιμοποιούμε. |
 |
|
 |
Βρες τον όγκο του παρακάτω σχήματος με μονάδα μέτρησης τους όγκους α, β και γ.
Ο όγκος του σχήματος θα είναι αντίστοιχα: 56α, 28β, 8γ. |
 |
Παρατηρούμε, ότι ο αριθμός που εκφράζει τον όγκο ενός στερεού εξαρτάται από τη μονάδα μέτρησης που χρησιμοποιούμε. |
|
|
|
 |
| Μονάδες μέτρησης μήκους |
- Η βασική μονάδα μήκους είναι το μέτρο (συμβολίζεται με m)
Υποδιαιρέσεις του μέτρου:
|
|
– 1 δεκατόμετρο ή παλάμη (dm) |
1dm = 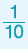 m = 0,1m m = 0,1m |
– 1 εκατοστόμετρο ή πόντος (cm) |
1cm =  m = 0,01m m = 0,01m |
− 1 χιλιοστόμετρο ή χιλιοστό (mm)
Πολλαπλάσια του μέτρου |
1mm = 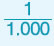 m = 0,001m m = 0,001m |
| − 1 χιλιόμετρο (Km) |
1Km = 1000m |
|
- Στη ναυσιπλοία, ως μονάδα μέτρησης μήκους, χρησιμοποιούμε το ναυτικό μίλι.
|
1 ναυτικό μίλι = 1.852 m |
|
|
Μονάδες μέτρησης εμβαδού
- Η βασική μονάδα μέτρησης εμβαδού είναι τo τετραγωνικό μέτρο (συμβολίζεται με m2) που είναι η επιφάνεια ενός τετραγώνου με πλευρά ένα μέτρο.
Υποδιαιρέσεις του τετραγωνικού μέτρου:
|
| − 1 τετραγωνικό δεκατόμετρο (dm2) |
1 dm2 =  m2 = 0,01 m2 m2 = 0,01 m2 |
| − 1 τετραγωνικό εκατοστόμετρο (cm2) |
1 cm2 = 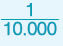 m2 =0,0001 m2 m2 =0,0001 m2 |
| − 1 τετραγωνικό χιλιοστόμετρο (mm2) |
1 mm2 = 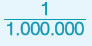 m2 =0,000001 m2 m2 =0,000001 m2 |
- Στην Ελλάδα ως μονάδα επιφανείας χρησιμοποιούμε το στρέμμα.
|
1 Km2 = 1.000.000 m2 = 106 m2
1 στρέμμα= 1000 m2 |
Μονάδες μέτρησης όγκου
- Η βασική μονάδα μέτρησης όγκου είναι τo κυβικό μέτρο (συμβολίζεται με m3) που είναι ο όγκος ενός κύβου ακμής ενός μέτρου.
Υποδιαιρέσεις του κυβικού μέτρου:
|
| − 1 κυβικό δεκατόμετρο (dm3) |
1 dm3 = 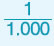 m3 = 0,001 m3 m3 = 0,001 m3 |
| − 1 κυβικό εκατοστόμετρο (cm3) |
1 cm3 = 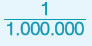 m3 =0,000001 m3 m3 =0,000001 m3 |
| − 1 κυβικό χιλιοστόμετρο (mm3) |
1 mm3 =  m3 =0,0000000001 m3 m3 =0,0000000001 m3 |
- Το dm3 ονομάζεται και λίτρο (lt) και
συνήθως χρησιμοποιείται για τη
μέτρηση όγκου υγρών.
|
1 lt = 1 dm3 = 0,001 m3 |
- To cm3 λέγεται χιλιοστόλιτρο (ml)
|
1 ml = 0,001 lt = 1cm3 = 0,000001 m3 |
Μονάδες μέτρησης χρόνου
- Η μονάδα μέτρησης του χρόνου είναι το δευτερόλεπτο (συμβολίζεται με s)
Πολλαπλάσια:
|
| - 1 λεπτό (min) |
|
|
|
|
= |
60 s |
| - 1 ώρα (h) |
|
|
= |
60 min |
= |
3.600 s |
| - 1 ημέρα |
= |
24 h |
= |
1.440 min |
= |
86.400 s |
Μονάδες μέτρησης μάζας
- Η βασική μονάδα μέτρησης μάζας είναι το χιλιόγραμμο ή κιλό (συμβολίζεται με Κg)
Υποδιαιρέσεις του κιλού:
|
| - 1 γραμμάριο (g) |
|
|
|
1 g |
= |
0,001 Kg |
| - 1 χιλιοστόγραμμο (mg) |
|
1 mg |
= |
0,001 g |
= |
0,000001 Kg |
| Πολλαπλάσιο του κιλού: |
| - 1 τόνος (t) |
|
1 t |
|
|
= |
1000 Kg |
|
|
| |
| ΠΑΡΑΔΕΙΓΜΑΤΑ - ΕΦΑΡΜΟΓΕΣ |
 |
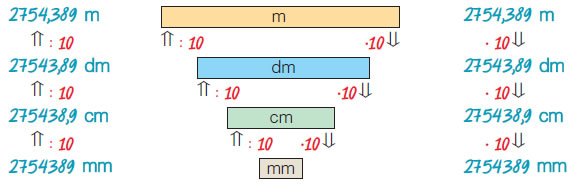
Να εκφραστεί το μήκος των 2.754,389 m, σε όλες τις υποδιαιρέσεις του m. |
 |
 |
|
| |
Για τις μετατροπές από μία μονάδα σε άλλη, φτιάχνουμε μια "σκάλα", που για να την "ανέβουμε", πρέπει από κάθε σκαλοπάτι στο επόμενο, να διαιρούμε με το 10, ενώ για να την "κατέβουμε" πρέπει να πολλαπλασιάσουμε με το 10.
|
 |
Η επιφάνεια ενός κύβου έχει εμβαδόν 96 cm2. Να βρεθεί ο όγκος του. |
 |
|
| |
Επειδή ο κύβος έχει 6 έδρες, η κάθε έδρα του θα έχει εμβαδόν 96 cm2 : 6 = 16 cm2 .
Αλλά είναι 16 cm2 = 4 cm  4 cm = (4 cm)2, άρα, η ακμή του κύβου είναι 4 cm. 4 cm = (4 cm)2, άρα, η ακμή του κύβου είναι 4 cm.
Επομένως, ο όγκος του κύβου είναι: (4 cm)3 = 4 cm  4 cm 4 cm  4 cm = 64 cm3 4 cm = 64 cm3 |
 |
| Μια αμαξοστοιχία διανύει την απόσταση Αθήνας - Πύργου σε 4 ώρες και 57 λεπτά. Αν η αμαξοστοιχία ξεκινά από την Αθήνα στις 9:10 π.μ., ποια ώρα θα φτάσει στον Πύργο; |
 |
|
 |
|
| |
Η αμαξοστοιχία θα φτάσει στις 9h 10min + 4h 57min = 13h 67min = 14h 7min, δηλαδή, θα φτάσει στον Πύργο στις 2:07 μ.μ., μετά το μεσημέρι. |
 |
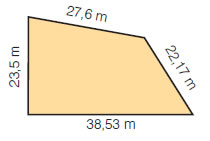
Να βρεθεί η περίμετρος του σχήματος: (α) σε μέτρα, (β) σε εκατοστά και (γ) σε χιλιόμετρα. |
 |
|
| |
| α) |
Η περίμετρος σε μέτρα είναι ίση με το άθροισμα των μηκών των πλευρών του, δηλαδή:
26,6 m + 23,5 m + 22,17 m + 38,53 m = 111,8 m. |
| (β) |
Είναι 111,8 m =111,8 m  0,001 = 0,1118 Km. 0,001 = 0,1118 Km. |
| (γ) |
Επίσης είναι 111,8 m  100 = 11180 cm. 100 = 11180 cm. |
|
 |
|
 |
Μια δεξαμενή νερού τρύπησε και χύνονται 2 σταγόνες κάθε δευτερόλεπτο. Αν οι 25 σταγόνες έχουν μάζα 1,5 g, να βρεθεί η μάζα του νερού που χάνεται κάθε ώρα. |
 |
|
| |
Κάθε δευτερόλεπτο χύνονται 2 σταγόνες νερού, άρα σε 1h = 3600s θα χυθούν: 3600  2 = 7200 σταγόνες νερού. 2 = 7200 σταγόνες νερού.
Αυτές θα έχουν μάζα: (7200 : 25)  1,5 g = 288 1,5 g = 288  1,5 g = 432 g = 0,432 Kg 1,5 g = 432 g = 0,432 Kg |
|
| |
| ΑΣΚΗΣΕΙΣ ΚΑΙ ΠΡΟΒΛΗΜΑΤΑ |
|
Να συμπληρώσεις τα κενά:
(α) 23 dm = …………… cm,
(β) 3,1 m = …………… Km,
(γ) 45,83 cm = …………… m,
(δ) 67,2 Κm = …………… mm,
(ε) 95,5 mm = …………… cm. |
 |
 |
Ένα ορθογώνιο παραλληλεπίπεδο έχει ακμές μήκους α = 3,1 m, β = 4,2 m και γ= 2,3 m. Να υπολογίσεις το μήκος των ακμών του σε mm και να το γράψεις σε τυποποιημένη μορφή. |
 |
Γράψε τα παρακάτω μήκη σε αύξουσα σειρά: 986 m, 0,023 Κm, 456 cm, 678 dm. |
 |
Ένα ορθογώνιο παραλληλόγραμμο έχει διαστάσεις πλευρών α = 23 cm και β = 45 cm. Να βρεις το εμβαδόν του, σε cm2και σε mm2. |
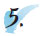 |
Συμπλήρωσε τα κενά: (α) 56 Κm2 = ……………… m22 (β) 0,987 στρέμματα = ………….. m2, (γ) 350 στρέμματα = …………….. m2. |
 |
Ένα οικόπεδο έχει σχήμα τετραγώνου με πλευρά 210 m. Να υπολογίσεις το εμβαδόν του σε m2 και σε στρέμματα. |
 |
Μια αυλή σχήματος ορθογωνίου παραλληλογράμμου, έχει διαστάσεις 5 m και 7,2 m. Θέλουμε να τη στρώσουμε, με τετράγωνες πλάκες, πλευράς 40 cm. Πόσες πλάκες θα χρειαστούμε; |
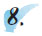 |
O όγκος ενός στερεού είναι 15 dm3 29 cm3. Να βρεις τον όγκο του στερεού σε cm3, m3 και mm3. |
 |
Ένας οινοπαραγωγός έχει αποθηκεύσει το κρασί του σε 3 ίσες δεξαμενές, σχήματος ορθογωνίου παραλληλεπιπέδου, με διαστάσεις 3 m, 2 m και 5 m. Αν πουλήσει το κρασί του προς 4 € το λίτρο, πόσα χρήματα θα εισπράξει; |
 |
Να υπολογίσεις τον χρόνο, από τις 8h 10min το πρωί, ως τις 5h 20min το απόγευμα. |
 |
Συμπλήρωσε τα κενά: (α) 4h 52min = ……… min=.......s, (β) 3h 12min = ……… min = ……… s (γ) 5h 20min 30s = ………… min = …………… s (δ) 56min 45s = ………… min = …………… s. |
 |
Nα υπολογίσεις: (α) το 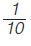 της ώρας, (β) το της ώρας, (β) το 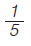 της ώρας, (γ) το της ώρας, (γ) το 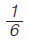 της ώρας. της ώρας.
|
 |
Διαθέτουμε σταθμά των 50 g, 500 g και δύο σταθμά του 1 Κg. Πώς θα ζυγίσουμε ένα βάρος (α) 3 Κg και 600 g και (β) 2 Κg και 450 g. |
 |
Πώς θα ζυγίσουμε (α) ένα σώμα μάζας 5 Κg, με σταθμά των 9 Κg, 3 Κg και 1 Κg (β) ένα σώμα μάζας 3 Κg, με σταθμά 10 Κg, 5 Κg και 1 Κg. |
 |
Διαθέτουμε τρία δοχεία που χωράνε 2 lt, 0,5 lt και 0,1 lt. Πώς θα μετρήσουμε ένα υγρό, όγκου (α) 5 lt, (β) 2,8 lt, (γ) 2,4 lt. |
 |
Σε μια πολυκατοικία θέλουν να κατασκευάσουν μια δεξαμενή που να χωράει 3 t πετρέλαιο και να έχει μήκος 2,5 m και πλάτος 1 m. Αν γνωρίζεις ότι ο 1 t πετρελαίου έχει όγκο 1200 lt, υπολόγισε το ύψος της δεξαμενής και πόσα lt πετρελαίου αντιστοιχούν σε κάθε cm ύψους; |
 |
Μια δεξαμενή έχει σχήμα ορθογωνίου παραλληλεπιπέδου με ύψος 1,2 m και βάση τετράγωνο πλευράς 80 cm. Μια αντλία αδειάζει από την δεξαμενή 8 lt το λεπτό. Να βρεθεί: (α) σε πόσο χρόνο η στάθμη του νερού θα κατέβει κατά 10 cm, (β) σε πόσο χρόνο θα αδειάσει η δεξαμενή και (γ) πόσο θα κατέβει η στάθμη του νερού σε μισή ώρα |
 |
| Ένας ποδηλάτης διήνυσε μια απόσταση σε χρόνο 1h 15 min, ενώ ένας δεύτερος διήνυσε την ίδια απόσταση σε χρόνο 1h 45min.
(α) Ποιο μέρος του χρόνου του δεύτερου είναι ο χρόνος του πρώτου ποδηλάτη; (β) Ποιο μέρος του
χρόνου του πρώτου είναι ο χρόνος του
δεύτερου ποδηλάτη; Τι παρατηρείς; |
 |
|
|
| |
 |
| |
| ΣΧΕΔΙΟ ΕΡΓΑΣΙΑΣ |
Ο άνθρωπος από τα πρώτα του βήματα φαίνεται να αναζήτησε τρόπους σύγκρουσης μεγεθών όπως είναι το μήκος, η επιφάνεια, ο όγκος, ο χρόνος και το βάρος ή η μάζα των διαφόρων αντικειμένων που χρησιμοποιούσε, αντάλλασσε, εμπορευόταν κ.λπ.
Οι ανθρώπινες επιλογές για τον καθορισμό των "μέτρων και σταθμών" είχαν ανέκαθεν και κοινωνικό, πολιτιστικό, οικονομικό, ιστορικό, επιστημονικό αλλά και πολιτικό χαρακτήρα. |
 |
- Προσπάθησε να βρεις και να καταγράψεις (σε ένα σχετικό πίνακα) τα "μέτρα και σταθμά" για τα βασικά μεγέθη (μήκος, επιφάνεια, όγκος, χρόνος και βάρος) που χρησιμοποιήθηκαν από το 3000 π.Χ. μέχρι σήμερα, από διάφορους λαούς (Αιγυπτίους, Βαβυλώνιους, Ινδούς, Κινέζους, Αρχαίους Έλληνες, Ρωμαίους, Άγγλους, Γάλλους, Ολλανδούς, Αμερικάνους, Ευρωπαίους και
Νεοέλληνες), τα οποία διατηρήθηκαν για μεγάλο χρονικό διάστημα, ώστε να είναι άξια λόγου για να αναφερθούν.
- Πότε, με ποιο τρόπο, για ποιο λόγο και από ποιους έγιναν προσπάθειες να επικρατήσει ένα διεθνές σύστημα μέτρησης μεγεθών; Γιατί απέτυχαν μερικές προσπάθειες από αυτές;
- Πόσο ρόλο έπαιξε στις τελικές επιλογές για τα «μέτρα και σταθμά» των βασικών μεγεθών, ο επιστημονικός παράγοντας;
- Ποια είναι η κατάσταση που επικρατεί σήμερα διεθνώς, για τα «μέτρα και σταθμά» των βασικών μεγεθών;
|
|
|