| Α.3.2. Πράξεις με δεκαδικούς αριθμούς - Δυνάμεις με βάση δεκαδικό αριθμό |
| Στους δεκαδικούς οι πράξεις δεν παρουσιάζουν καμιά ιδιαίτερη δυσκολία. Αρκεί να προσέχουμε τη θέση της υποδιαστολής. Ας τις δούμε, όμως, πιο αναλυτικά. |
| |
|
 |
- Η Πρόσθεση και η Αφαίρεση δεκαδικών αριθμών γίνεται, όπως και στους φυσικούς αριθμούς.
Προσθέτουμε ή αφαιρούμε τα ψηφία της ίδιας τάξης, τοποθετώντας τους αριθμούς τον ένα κάτω από τον άλλο έτσι, ώστε οι υποδιαστολές να γράφονται στην ίδια στήλη.
|
 |
- Ο Πολλαπλασιασμός δεκαδικών αριθμών γίνεται, όπως και των φυσικών αριθμών.
Τοποθετούμε στο αποτέλεσμα της πράξης την υποδιαστολή τόσες θέσεις από τα δεξιά προς τα αριστερά, όσα είναι συνολικά τα ψηφία στα δεκαδικά μέρη και των δύο παραγόντων.
|
 |
-
Η Διαίρεση δεκαδικού αριθμού με δεκαδικό αριθμό γίνεται, όπως και η ευκλείδεια διαίρεση.
Πολλαπλασιάζουμε το διαιρέτη και το διαιρετέο με την κατάλληλη δύναμη του 10 έτσι, ώστε ο διαιρέτης να γίνει φυσικός αριθμός.
Όταν εξαντληθεί το ακέραιο μέρος του διαιρετέου, "κατεβάζουμε" το μηδέν, ως πρώτο δεκαδικό ψηφίο από τον διαιρετέο και τοποθετούμε στο πηλίκο υποδιαστολή.
|
 |
- Όταν πολλαπλασιάζουμε με 0,1, 0,01, 0,001… ή όταν διαιρούμε ένα δεκαδικό αριθμό με 10, 100, 1000, … μεταφέρουμε την υποδιαστολή προς τα αριστερά μια, δυο, τρεις, … αντίστοιχα θέσεις.
|
258  0,1 = 258 ή 258 : 10 = 25,8 0,1 = 258 ή 258 : 10 = 25,8
8,45  0,01 = 0,0845 ή 0,01 = 0,0845 ή
8,45 : 100 = 0,0845
12,45  0,001 = 0,01245 ή 0,001 = 0,01245 ή
12,45 : 1000 = 0,01245 |
- Όταν πολλαπλασιάζουμε ένα δεκαδικό αριθμό με 10, 100, 1000… μεταφέρουμε την υποδιαστολή του αριθμού προς τα δεξιά μία, δύο, τρεις, … θέσεις αντίστοιχα.
|
28,34  10 = 283,4 10 = 283,4
38,0945  100 = 3809,45 100 = 3809,45
1,3245  1000 = 1324,5 1000 = 1324,5
0,009  1000 = 9 1000 = 9 |
- Οι Δυνάμεις των δεκαδικών αριθμών έχουν τις ιδιότητες των δυνάμεων των φυσικών αριθμών.
Το πλήθος των δεκαδικών ψηφίων, που έχει το αποτέλεσμα, προκύπτει από το πλήθος των δεκαδικών ψηφίων της βάσης επί τον εκθέτη της δύναμης.
|
| (2,5)2 =2,52=6,25 |
1 x 2 = 2 |
| (1,25)2 =1,252=1,5625 |
2 x 2 = 4 |
| (0,115)2 =0,1152=0,013225 |
3 x 2 = 6 |
| (1,5)3 =1,53=3,375 |
1 x 3 = 3 |
| (0,15)3 =0,153=0,003375 |
2 x 3 = 6 |
| (0,5)4 =0,54=0,0625 |
1 x 4 = 4 |
| (0,15)4 =0,154=0,00050625 |
2 x 4 = 8 |
|
|
|
| |
 ΑΣΚΗΣΕΙΣ ΚΑΙ ΠΡΟΒΛΗΜΑΤΑ ΑΣΚΗΣΕΙΣ ΚΑΙ ΠΡΟΒΛΗΜΑΤΑ |
|
|
|
Να υπολογίσεις τα αθροίσματα: (α) 48,18 + 3,256 + 7,129 (β) 3,59 + 7,13 + 8,195.
Μικροπείραμα  |
|
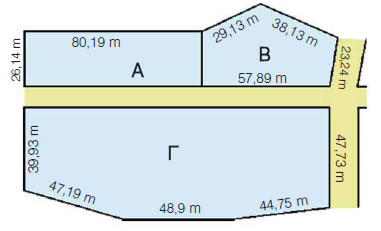
Να υπολογίσεις το μήκος της περιμέτρου καθενός από τα οικόπεδα του παρακάτω σχήματος. |
 |
 |
Να υπολογίσεις τις διαφορές:
(α) 15,833 - 4,791
(β) 13,902 - 12,5025
(γ) 20,0005 - 12,501. |
 |
Να κάνεις τις παρακάτω διαιρέσεις: (α) 579 : 48 (β) 314 : 25 (γ) 520 : 5,14 (δ) 49,35 : 7 |
 |
Να κάνεις τις πράξεις: (α) 520 $\cdot$ 0,1 + 0,32 $\cdot$ 100 (β) 4,91 $\cdot$ 0,01 + 0,819 $\cdot$ 10. |
 |
Να κάνεις τις πράξεις: (α) 4,7 : 0,1 – 45 : 10 (β) 0,98 : 0,0001 – 6785 : 1000 |
 |
Η περίμετρος ενός τετραγώνου είναι 20,2. Να υπολογίσεις την πλευρά του. |
 |
Η περίμετρος ενός ισοσκελούς τριγώνου είναι 48,52. Αν η βάση του είναι 10,7, πόσο είναι η κάθε μία από τις ίσες πλευρές του; |
 |
Να υπολογίσεις τις τιμές των αριθμητικών παραστάσεων: (α) 24 $\cdot$ 5 – 2 + 3 $\cdot$ 5 (β) 3 $\cdot$ 11 – 2 + 54,1 : 2. |
 |
Να υπολογίσεις τις δυνάμεις: (α) 3,12 (β) 7,012 (γ) 4,52 (δ) 0,52 (ε) 0,22 (στ) 0,33. |
 |
| Τοποθέτησε ένα "x" στην αντίστοιχη θέση |
ΣΩΣΤΟ |
ΛΑΘΟΣ |
| (α) |
2,75 + 0,05 + 1,40 + 16,80 = 21 |
|
|
| (β) |
420,510 + 72,490 + 45,19 + 11,81 = 500 |
|
|
| (γ) |
4 – 3,852 = 1,148 |
|
|
| (δ) |
32,01 – 4,001 = 28,01 |
|
|
| (ε) |
41900 $\cdot$ 0,0001 – 0,0419 $\cdot$ 1000 = 0
| |
|
| (στ) |
56,89 $\cdot$0,01 + 4311 : 10000 = 1 |
|
|
| (ζ) |
(3,2 + 7,2 $\cdot$ 2 + 24 $\cdot$ 0,1) : 100 = 0,2 |
|
|
|
|
|