| Α.2.4. Πρόσθεση και Αφαίρεση κλασμάτων |
| |
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ 1η |
|
| Σκεφτόμαστε |
|
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ 2η |
|
| ΔΡΑΣΤΗΡΙΟΤΗΤΑ 3η |
| |
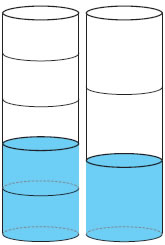
Μια βρύση γεμίζει, σε 1 ώρα, τα 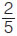 της δεξαμενής. Μια άλλη βρύση γεμίζει το της δεξαμενής. Μια άλλη βρύση γεμίζει το 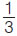 της ίδιας δεξαμενής, επίσης σε 1 ώρα. της ίδιας δεξαμενής, επίσης σε 1 ώρα.
- Αν και οι δύο βρύσες τρέχουν ταυτόχρονα μέσα στη δεξαμενή, τι μέρος της δεξαμενής θα γεμίσουν σε 1 ώρα;
|
 |
| Σκεφτόμαστε |
|
Αν οι βρύσες "τρέχουν" ταυτόχρονα στη δεξαμενή για 1 ώρα θα έχουν γεμίσει ένα τμήμα της που αντιστοιχεί στο άθροισμα των τμημάτων αυτής που η κάθε μία γεμίζει ξεχωριστά. Δηλαδή το ... |
|
Μικροπείραμα  |
|
|
| |
| ΠΑΡΑΔΕΙΓΜΑΤΑ - ΕΦΑΡΜΟΓΕΣ |
 |
Να υπολογισθεί το άθροισμα 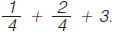 |
 |

|
Μετατρέπουμε το φυσικό αριθμό σε κλάσμα με παρονομαστή 4.
Είναι: 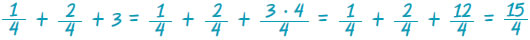 |
 |
Να αποδειχθεί ότι: 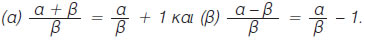 |
 |

|
 |
Να υπολογισθεί η διαφορά και το άθροισμα των κλασμάτων 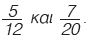 |
 |
Τα κλάσματα είναι ετερώνυμα και πρέπει πρώτα να μετατραπούν σε ισοδύναμα ομώνυμα.
Έχουμε: ΕΚΠ(12, 20) = 60 οπότε: 60 : 12 = 5 και 60 : 20 = 3
Άρα: 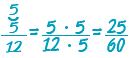 και και 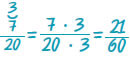 . Επειδή . Επειδή 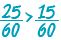 μπορεί να υπολογιστεί μπορεί να υπολογιστεί
η διαφορά: 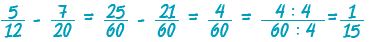
και 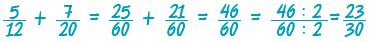 |
 |
Να βρεθεί η διαφορά: 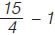 και το αποτέλεσμα να γίνει μεικτός. και το αποτέλεσμα να γίνει μεικτός. |
 |
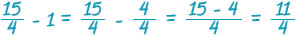 . Για να τρέψουμε το αποτέλεσμα σε μεικτό αριθμό εκτελούμε την ευκλείδεια διαίρεση: 11 = 4 · 2 + 3 και έχουμε: . Για να τρέψουμε το αποτέλεσμα σε μεικτό αριθμό εκτελούμε την ευκλείδεια διαίρεση: 11 = 4 · 2 + 3 και έχουμε:
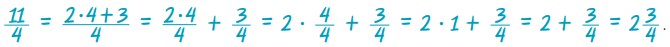
|
 |
Να βρεθεί το άθροισμα: 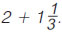 |
 |
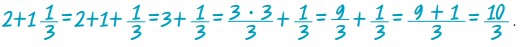
|
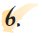 |
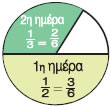 Την πρώτη ημέρα ένας κηπουρός κούρεψε το γκαζόν στο Την πρώτη ημέρα ένας κηπουρός κούρεψε το γκαζόν στο 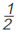 μιας στρογγυλής πλατείας. Την δεύτερη ημέρα, εξαιτίας μιας δυνατής βροχής, κατάφερε να κουρέψει μόνο το μιας στρογγυλής πλατείας. Την δεύτερη ημέρα, εξαιτίας μιας δυνατής βροχής, κατάφερε να κουρέψει μόνο το 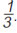 του αρχικού γκαζόν. Ποιό μέρος από το γκαζόν της πλατείας κουρεύτηκε μέχρι και το τέλος της δεύτερης ημέρας; του αρχικού γκαζόν. Ποιό μέρος από το γκαζόν της πλατείας κουρεύτηκε μέχρι και το τέλος της δεύτερης ημέρας;
|
 |
Για να βρούμε το μέρος της πλατείας που κουρεύτηκε, στο τέλος της δεύτερης ημέρας, δεν έχουμε παρά να προσθέσουμε τα δύο κλάσματα, δηλαδή το 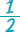 και το και το 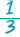 . Αλλά, για να εκτελέσουμε αυτή την πρόσθεση πρέπει να μετατρέψουμε τα δύο κλάσματα σε ομώνυμα. Άρα, θα έχουμε: . Αλλά, για να εκτελέσουμε αυτή την πρόσθεση πρέπει να μετατρέψουμε τα δύο κλάσματα σε ομώνυμα. Άρα, θα έχουμε: 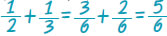 . Για να βρούμε ποιο κλάσμα της πλατείας έχει απομείνει για κούρεμα, πρέπει να αφαιρέσουμε από το όλο μέρος, δηλαδή: . Για να βρούμε ποιο κλάσμα της πλατείας έχει απομείνει για κούρεμα, πρέπει να αφαιρέσουμε από το όλο μέρος, δηλαδή: 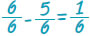 |
|
Μικροπείραμα  |
|
| |
| ΑΣΚΗΣΕΙΣ ΚΑΙ ΠΡΟΒΛΗΜΑΤΑ |
|
| |
ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ ΓΙΑ ΤΟ ΣΠΙΤΙ |
|
| |
 ΝΟΤΕΣ ΚΑΙ ΚΛΑΣΜΑΤΑ ΝΟΤΕΣ ΚΑΙ ΚΛΑΣΜΑΤΑ
|
Ανάμεσα στα κοινά στοιχεία όλων των ανθρωπίνων πολιτισμών είναι η δυνατότητα αρίθμησης και μουσικής έκφρασης.
- Ο άνθρωπος δημιουργεί μουσική, ήδη, από τους προϊστορικούς χρόνους, αφού το αρχαιότερο σχετικό εύρημα, που έχει ηλικία 35.000 χρόνων, είναι οστά από μαμούθ τα οποία χρησιμοποιήθηκαν για την παραγωγή ρυθμικών ήχων.
- Οι μελέτες έχουν δείξει, ότι η έννοια του αριθμού εμφανίζεται στον άνθρωπο από τα πρώτα του βήματα. Διαπιστώθηκε ότι αυτή η πρώιμη ικανότητα αρίθμησης σχετίζεται με την ικανότητα της κατάτμησης του χρόνου, που δημιουργεί η αντιστοιχία γεγονότων και χρονικών στιγμών και μάλιστα χωρίς, τη χρήση της έννοιας του αριθμού. Εξάλλου η αρίθμηση είναι μια πολιτιστική αναγκαιότητα, ένα καθολικό στοιχείο πολιτισμού.
Η συνάντηση της Μουσικής με τα Μαθηματικά πραγματοποιείται μέσα από την αίσθηση, που έχουμε για τον χρόνο και εντοπίζεται σε δύο βασικούς άξονες κάθε μουσικής έκφρασης, το Ρυθμό και την Αρμονία. Ο άνθρωπος έχει την ικανότητα να εντοπίζει και να απομονώνει τις χρονικές στιγμές. Το διάστημα που μεσολαβεί μεταξύ δύο στιγμών, δημιουργεί την αίσθηση της διάρκειας. Ο χωρισμός του χρόνου από τα γεγονότα δημιουργεί ένα πυκνό σύνολο από στιγμές. Έτσι, ο ρυθμός και ο αριθμός έχουν κοινή καταγωγή, το χωρισμό του χρόνου σε στιγμές και την αντιστοίχιση των χρονικών στιγμών με γεγονότα. Ο ρυθμός είναι από τις πρώτες μουσικές ανθρώπινες κατακτήσεις, όπως ακριβώς ο αριθμός είναι από τις πρώτες θεμελιώδεις Μαθηματικές ανθρώπινες επινοήσεις. Ο ρυθμός, λοιπόν, είναι το πρώτο είδος μουσικής που δημιούργησε ο άνθρωπος. Το μουσικό μέτρο, το οποίο είναι απαραίτητο για την εκτέλεση ενός μουσικού θέματος, δηλώνεται με ένα κλάσμα που καθορίζει το ρυθμό. Σήμερα οι δύο αυτές έννοιες, του ρυθμού και του αριθμού - κλάσματος, συνυπάρχουν στον τρόπο με τον οποίο γράφεται η Δυτική Μουσική. Ας δούμε ένα παράδειγμα: Στο σχήμα φαίνεται ένα μέρος ενός μουσικού κομματιού. Η χρονική αξία του πρώτου και δεύτερου συμβόλου είναι 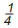 και και 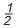 αντίστοιχα, ενώ κάθε ένα από τα σύμβολα (νότες), που είναι ενωμένα έχουν εξ ορισμού αξία αντίστοιχα, ενώ κάθε ένα από τα σύμβολα (νότες), που είναι ενωμένα έχουν εξ ορισμού αξία 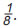 Το κλάσμα Το κλάσμα 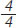 στην αρχή καθορίζει πως κάθε μέτρο, κάθε διάστημα δηλαδή, το οποίο περιέχει μια μουσική φράση, πρέπει να περιέχει σύμβολα (νότες) συνολικής αξίας στην αρχή καθορίζει πως κάθε μέτρο, κάθε διάστημα δηλαδή, το οποίο περιέχει μια μουσική φράση, πρέπει να περιέχει σύμβολα (νότες) συνολικής αξίας 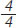 . Πράγματι εικόνα . Πράγματι εικόνα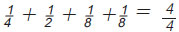 . Με αυτόν τον τρόπο ο αριθμός - κλάσμα καθορίζει το ρυθμό και επιτρέπει να εκτελείται ένα μουσικό κομμάτι συγχρονισμένα από τους μουσικούς. . Με αυτόν τον τρόπο ο αριθμός - κλάσμα καθορίζει το ρυθμό και επιτρέπει να εκτελείται ένα μουσικό κομμάτι συγχρονισμένα από τους μουσικούς. |
| |
| ΣΧΕΔΙΟ ΕΡΓΑΣΙΑΣ |
- Βρες παρτιτούρες από τραγούδια με διαφορετικούς ρυθμούς και γράψε τα κλάσματα, που αντιστοιχούν στους ρυθμούς των τραγουδιών αυτών.
- Αναζήτησε και βρες ορισμένα χαρακτηριστικά τραγούδια με διαφορετικούς ρυθμούς και προσπάθησε να συσχετίσεις τα κλάσματα, που αντιστοιχούν στους ρυθμούς αυτούς, με την ονομασία του εκάστοτε συγκεκριμένου ρυθμού
|
 |
|
|