7-8 ΣΩΜΑΤΙΔΙΟ ΠΑΓΙΔΕΥΜΕΝΟ ΣΕ ΠΗΓΑΔΙ ΔΥΝΑΜΙΚΟΥ

Σχ. 7.11 (α) Η διάταξη αυτή περιορίζει τα ελεύθερα ηλεκτρόνια του αγωγού σ' ένα μήκος L πάνω στον άξονα των x. (β) Το πηγάδι δυναμικού που δημιουργεί η διάταξή μας. Τα ελεύθερα ηλεκτρόνια που βρίσκονται στα όρια του L έχουν δυναμική ενέργεια, U=0 ενώ έξω από τα όρια του L δυναμική ενέργεια U ≠ 0. Για να βγει ένα ηλεκτρόνιο από το πηγάδι πρέπει να έχει κινητική ενέργεια μεγαλύτερη από το βάθος του πηγαδιού U₀. Στην πράξη το πηγάδι δυναμικού που δημιουργεί η διάταξή μας έχει στρογγυλεμένα χείλη και τοιχώματα που γέρνουν ελαφρά προς τα έξω.

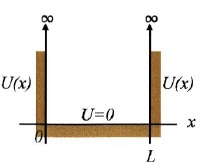Σχ. 7.12

Σωματίδιο παγιδευμένο σε πηγάδι δυναμικού είναι ένα σωματίδιο που λόγω εξωτερικών δυνάμεων είναι παγιδευμένο σε μία περιοχή του χώρου. Αν θεωρήσουμε για παράδειγμα σαν σωμάτιο ένα ηλεκτρόνιο, τέτοιου είδους παγίδες είναι τα άτομα. Η διάταξη του σχήματος 7.11 μας δίνει μια πιο χειροπιαστή εικόνα του τι είναι ένα πηγάδι δυναμικού.

Α) ΠΗΓΑΔΙ ΔΥΝΑΜΙΚΟΥ ΑΠΕΙΡΟΥ ΒΑΘΟΥΣ

Έστω ότι έχουμε ένα ηλεκτρόνιο που κινείται μόνο κατά τη διεύθυνση των x και είναι παγιδευμένο σ' ένα πηγάδι δυναμικού άπειρου βάθους όπως στο σχήμα 7.12. Αυτό σημαίνει ότι εάν το ηλεκτρόνιο βρίσκεται στο διάστημα 0 ≤ x ≤ L έχει δυναμική ενέργεια U=0 ενώ αν x < 0 ή x > L η δυναμική ενέργεια απειρίζεται.

Με τους παραπάνω περιορισμούς η λύση της εξίσωσης (7.6) είναι

Ψ(x) = 0 αν x<0 ή x>L και

Ψ(x) = Αημ για 0≤ x≤ L όπου n=1,2,3....

Η Ψ(x) είναι η κυματοσυνάρτηση που περιγράφει το ηλεκτρόνιο μας για κάποια δεδομένη χρονική στιγμή.

Το μήκος κύματος της ημιτονοειδούς αυτής μορφής μπορεί να πάρει τις τιμές

λ = (n=1,2,3....)

Αν θέσουμε τις τιμές του λ που βρήκαμε στη σχέση p=h/λ προκύπτει

Εικόνα (7.7)

Βλέπουμε ότι η ορμή του ηλεκτρονίου δεν μπορεί να πάρει οποιαδήποτε τιμή αλλά τιμές που είναι ακέραια πολλαπλάσια της ποσότητας h/2L. Δηλαδή η ορμή είναι κβαντισμένη.

Κάτι αντίστοιχο συμβαίνει και με την ενέργεια του ηλεκτρονίου που μπορεί να είναι μόνο κινητική. E=K =
Αντικαθιστώντας στη σχέση αυτή την ορμή από την (7.7) βρίσκουμε

Εικόνα (7.8)

Η ενέργεια του ηλεκτρονίου μας είναι υποχρεωτικά κβαντισμένη.

Ας δούμε τώρα αν μπορούμε να εντοπίσουμε τη θέση του ηλεκτρονίου.

Είδαμε ότι, σύμφωνα με την παραδοχή του Born, το τετράγωνο του μέτρου της κυματοσυνάρτησης είναι η πιθανότητα θέσης ανά μονάδα όγκου. Στο πρόβλημα που μελετάμε το ηλεκτρόνιο κινείται μόνο στη διεύθυνση του άξονα των x.

Άρα το |Ψ(x)|² θα είναι η πιθανότητα θέσης ανά μονάδα μήκους για τη δεδομένη στιγμή που εξετάζουμε.

Σχ. 7.13 (α) Γραφικές παραστάσεις της Ψ(x) για τους τρεις πρώτους κβαντικούς αριθμούς .(β) Οι αντίστοιχες παραστάσεις για το |Ψ(x)|². Η τιμή του |Ψ(x)|² για κάθε σημείο δείχνει την πιθανότητα να βρεθεί το ηλεκτρόνιο σ' ένα στοιχειώδες dx γύρω από το σημείο αυτό. (γ) Οι αντίστοιχες ενεργειακές στάθμες του ηλεκτρονίου. Η απόσταση ανάμεσα σε δύο διαδοχικές στάθμες δεν είναι σταθερή, μεγαλώνει όσο αυξάνει το n

Σχ. 7.14

Σχ. 7.15

Σχ. 7.15

Β. ΠΗΓΑΔΙ ΠΕΠΕΡΑΣΜΕΝΟΥ ΒΑΘΟΥΣ
Έστω ότι το ηλεκτρόνιο της προηγούμενης παραγράφου είναι εγκλωβισμένο σ' ένα πηγάδι πεπερασμένου βάθους (σχ. 7.14). Τώρα, αν το ηλεκτρόνιο βρίσκεται στο διάστημα [0-L] έχει δυναμική ενέργεια U= 0, αν βρίσκεται έξω από το διάστημα [0-L] έχει δυναμική ενέργεια U₀. Το ηλεκτρόνιο που εξετάζούμε έχει ενέργεια μικρότερη από U₀. Με αυτές τις οριακές συνθήκες, η 7.6, για 0≤x≤L έχει μια ημιτονοειδή λύση ανάλογη με αυτή που βρήκαμε στο πηγάδι άπειρου βάθους. Για x<0 και x>L όμως, δεν προκύπτει Ψ(x) = 0, όπως πριν, αλλά μία εκθετικά φθίνουσα συνάρτηση του x. Τελικά η κυματοσυνάρτηση έχει μία μορφή σαν αυτήν του σχήματος 7.15.

Και στην περίπτωση του πηγαδιού πεπερασμένου βάθους οι καταστάσεις στις οποίες μπορεί να βρεθεί το ηλεκτρόνιο είναι διακριτές (κβαντισμένες). Εκεί που μας περιμένει μία κβαντική έκπληξη είναι στη γραφική παράσταση του |Ψ(x)|² συναρτήσει του x. Βλέπουμε ότι το |Ψ(x)|² δε μηδενίζεται αμέσως για x < 0 και x > L. Δηλαδή ακόμη κι αν το ηλεκτρόνιο δεν έχει την απαιτούμενη κινητική ενέργεια για να βγει από το πηγάδι, σύμφωνα με τις προβλέψεις της κλασικής θεωρίας, υπάρχει κάποια πιθανότητα να βρεθεί έξω απ' αυτό.

Σχ. 7.16 (α) Γραφικές παραστάσεις της Ψ (χ) για τους τρεις πρώτους κβαντικούς αριθμούς, (β) Οι αντίστοιχες ενεργειακές στάθμες ταυ ηλεκτρονίου, (γ) Οι αντίστοιχες παραστάσεις για το |Ψ(x)|2 . Η τιμή του |Ψ(x)|2 για κάθε σημείο δείχνει την πιθανότητα να βρεθεί το ηλεκτρόνιο σ' ένα στοιχειώδες dx γύρω από το σημείο αυτό. Βλέπουμε ότι οι καμπύλες εκτείνονται και έξω από τα όρια του πηγαδιού.

Σχ. 7.16 (α) Γραφικές παραστάσεις της Ψ (x) για τους τρεις πρώτους κβαντικούς αριθμούς, (β) Οι αντίστοιχες ενεργειακές στάθμες ταυ ηλεκτρονίου, (γ) Οι αντίστοιχες παραστάσεις για το |Ψ(x)|² . Η τιμή του |Ψ(x)|² για κάθε σημείο δείχνει την πιθανότητα να βρεθεί το ηλεκτρόνιο σ' ένα στοιχειώδες dx γύρω από το σημείο αυτό. Βλέπουμε ότι οι καμπύλες εκτείνονται και έξω από τα όρια του πηγαδιού.

Ας συνοψίσουμε όσα έχουμε μάθει μέχρι τώρα :

1. Το ηλεκτρόνιο - αντίθετα με ό,τι προβλέπει η κλασική θεωρία – δε μπορεί να έχει οποιαδήποτε τιμή ενέργειας ή ορμής όταν βρίσκεται μέσα στο πηγάδι.
2. Το ηλεκτρόνιο δεν ηρεμεί μέσα στην παγίδα του. Η χαμηλότερη στάθμη κινητικής ενέργειας στην οποία μπορεί να βρεθεί αντιστοιχεί σε n=1 και είναι διάφορη του μηδενός. Είναι κάτι που έρχεται σε αντίθεση με την κλασική θεωρία.
3. Το ηλεκτρόνιο είναι πιθανότερο να βρεθεί σε ορισμένα τμήματα της παγίδας απ' ό,τι σε άλλα. Αν βρίσκεται στη θεμελιώδη κατάσταση (n=1 ) (αναφέρεται και σαν εδαφική κατάσταση) είναι πολύ πιθανότερο να

βρεθεί γύρω από το μέσον της παγίδας παρά κοντά στα άκρα της. Μόνο για ψηλές ενεργειακές στάθμες η πιθανότητα να βρίσκεται σε κάποια θέση κατανέμεται πιο ομοιόμορφα και συγκλίνει στην άποψη της κλασικής θεωρίας που θεωρεί όλες τις θέσεις εξίσου πιθανές.
4. Το ηλεκτρόνιο μπορεί να διαφύγει από την παγίδα του. Εάν το πηγάδι του δυναμικού δεν έχει άπειρο βάθος το ηλεκτρόνιο έχει κάποια πιθανότητα (μικρή αλλά όχι μηδενική) να βρεθεί έξω από το πηγάδι κι ας μην έχει την θεωρητικά απαιτούμενη ενέργεια για να συμβεί αυτό. Η πιθανότητα αυτή μεγαλώνει όσο το ηλεκτρόνιο βρίσκεται σε ψηλότερη ενεργειακή στάθμη.