 Εικ. 7.2 Wilchelm Rontgen (1845- 1923). Ολλανδία, Ελβετία, Γερμανία. Η ανακάλυψη των ομώνυμων ακτίνων έφερε επανάσταση στην ιατρική. Νόμπελ Φυσικής το 1902.
 Εικ. 7.3 Arthur Holly Compton (1892-1962) Αμερική. |
7-4 ΤΟ ΦΑΙΝΟΜΕΝΟ COMPTON
Οι ακτίνες Χ Το 1895 ο Wilchelm Rontgen (Ρέντγκεν) ανακάλυψε ότι όταν ένα μέταλλο «βομβαρδιστεί» με ηλεκτρόνια που κινούνται με μεγάλη ταχύτητα εκπέμπει ηλεκτρομαγνητική ακτινοβολία. Η ακτινοβολία αυτή ονομάστηκε ακτίνες Χ ή ακτίνες Rontgen. Ακτίνες Χ χρησιμοποιούνται καθημερινά σήμερα για την λήψη κοινών ακτινογραφιών. Οι ακτίνες Χ έχουν μήκη κύματος από 0,001 nm, έως 1 nm . Ο μηχανισμός παραγωγής των ακτίνων Χ είναι ακριβώς ο αντίστροφος του φωτοηλεκτρικού φαινομένου. Στο φωτοηλεκτρικό φαινόμενο μια μεταλλική επιφάνεια «βομβαρδίζεται» με ηλεκτρομαγνητικό κύμα και εκπέμπει ηλεκτρόνια. Στις ακτίνες Χ η μεταλλική επιφάνεια «βομβαρδίζεται» με ηλεκτρόνια και εκπέμπει ηλεκτρομαγνητικό κύμα. Όταν τα ηλεκτρόνια της δέσμης φτάνουν στην επιφάνεια του μετάλλου επιβραδύνονται απότομα. Η επιβράδυνση αυτή συνοδεύεται από εκπομπή ακτινοβολίας, το φωτόνιο της οποίας θα έχει ενέργεια μικρότερη ή ίση με την ενέργεια του ηλεκτρονίου στο οποίο οφείλεται η εκπομπή του. Υπάρχει και άλλη αιτία για την οποία εκπέμπεται ακτινοβολία από τη μεταλλική επιφάνεια. Καθώς τα ηλεκτρόνια συγκρούονται με τα άτομα της επιφάνειας του μετάλλου τούς μεταφέρουν ενέργεια. Τα άτομα διεγείρονται, τα ηλεκτρόνιά τους δηλαδή μεταφέρονται σε στιβάδες μεγαλύτερης ενέργειας. Όταν αποδιεγείρονται, όταν δηλαδή τα ηλεκτρόνια επανέλθουν στην αρχική τους στιβάδα, εκπέμπουν στο περιβάλλον ενέργεια υπό μορφή ηλεκτρομαγνητικής ακτινοβολίας. Η ύπαρξη φωτονίων επιβεβαιώθηκε πειραματικά το 1924 από τον Αμερικανό Arthur Holly Compton. Ο Compton παρατήρησε ότι όταν ακτίνες Χ προσπίπτουν πάνω σε μια υλική επιφάνεια ένα μέρος τους εκτρέπεται από τα σωματίδια της ύλης (σκεδάζεται). Ο Compton διαπίστωσε ότι το σκεδαζόμενο τμήμα της ακτινοβολίας έχει μήκος κύματος μεγαλύτερο από το μήκος κύματος της προσπίπτουσας ακτινοβολίας (μικρότερη συχνότητα). Οι μετρήσεις του Compton έδειξαν ότι η μεταβολή του μήκους κύματος ανάμεσα στην προσπίπτουσα και τη σκεδαζόμενη δέσμη εξαρτάται μόνο από τη γωνία ανάμεσα στις δύο δέσμες και μάλιστα υπακούει στη σχέση
Σύμφωνα με την κλασική θεωρία ένα ηλεκτρομαγνητικό κύμα συχνότητας f που προσπίπτει σ' ένα υλικό αναγκάζει τα ηλεκτρόνια του υλικού να ταλαντώνονται με την ίδια συχνότητα και, επακόλουθα, να παράγουν με τη σειρά τους σαν μικρές κεραίες, ηλεκτρομαγνητικό κύμα της ίδιας συχνότητας f. Η κλασική θεωρία, λοιπόν, θα περίμενε η σκεδαζόμενη δέσμη να έχει την ίδια συχνότητα και, αντίστοιχα, ίδιο μήκος κύματος με την προσπίπτουσα δέσμη. |
Τα πράγματα φωτίζονται αν δούμε την ηλεκτρομαγνητική ακτινοβολία ως ρεύμα φωτονίων, δηλαδή σωματίων με μηδενική μάζα ηρεμίας που μεταφέρουν ενέργεια και ορμή. Τότε το πρόβλημα της σκέδασης της ακτινοβολίας μετατρέπεται σε πρόβλημα κρούσης ανάμεσα σ' ένα φωτόνιο και ένα ηλεκτρόνιο. Ας υποθέσουμε ότι ένα φωτόνιο μήκους κύματος λ συγκρούεται μ' ένα πρακτικώς ακίνητο ηλεκτρόνιο (σχ. 7.7). Μετά τη σκέδαση το φωτόνιο κινείται σχηματίζοντας γωνία ψ με την αρχική διεύθυνση κίνησης και έχοντας χάσει τμήμα της αρχικής του ενέργειας αφού ένα μέρος της αρχικής του ενέργειας θα μεταφερθεί στο ηλεκτρόνιο. Το σκεδαζόμενο φωτόνιο θα έχει μετατραπεί σε φωτόνιο μήκους κύματος λ' με λ' > λ. Κατά τη διάρκεια της σκέδασης πρέπει να διατηρούνται η ενέργεια και η ορμή του συστήματος. Σχ. 7.7 Το φωτόνιο έχει πριν τη σκέδαση ενέργεια Ε = hf = hc/λ και μετά τη σκέδαση Ε' = hc/λ' .Θα πρέπει λοιπόν να ισχύει
όπου Ke η κινητική ενέργεια του ανακρουσμένου ηλεκτρονίου. Επειδή το ηλεκτρόνιο μετά την κρούση μπορεί να κινείται με ταχύτητα που πλησιάζει την ταχύτητα του φωτός καλό είναι να χρησιμοποιήσουμε τη σχέση 6.17 για την κινητική του ενέργεια οπότε
Η ορμή του φωτονίου πριν είναι p = E/c = h/λ και η ορμή του φωτονίου μετά είναι p' = h/λ'. Η ορμή του ηλεκτρονίου θα είναι σύμφωνα με τη σχέση (6.15) pe= p = p' + pe pe = p - p' Χρησιμοποιώντας τον νόμο του συνημίτονου στο διανυσματικό διάγραμμα του σχήματος 7.8 προκύπτει pc2 = p2 + p'2 - 2pp'συνφ Δηλαδή |
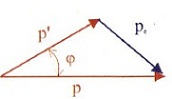 Σχ. 7.8. |
ΠΑΡΑΔΕΙΓΜΑ 7-2
Δέσμη ακτίνων X με λ = 0,1nm (10-10m) σκεδάζεται από επιφάνεια άνθρακα. Η σκεδασθείσα δέσμη σχηματίζει γωνία 90° με την προσπίπτουσα. Να βρεθούν : Απάντηση α) Ε = hf = p = β) λ' - λ = άρα λ' = λ + E' = p' = h/λ' = γ) Ke = E - E' = 291 eV |