4-8 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΣΤΡΟΦΟΡΜΗΣ

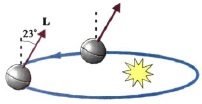
Σχ. 4.29 Η στροφορμή της Γης -λόγω της ιδιοπεριστροφής της- διατηρείται σταθερή

Στη στροφική κίνηση ισχύει ένας νόμος διατήρησης, ανάλογος με το νόμο διατήρησης της ορμής που ισχύει στη μεταφορική κίνηση. Το μέγεθος που διατηρείται στη στροφική κίνηση είναι η στροφορμή.

Η διατήρηση της στροφορμής σε ένα σώμα

Αν σε ένα σώμα το αλγεβρικό άθροισμα των ροπών είναι μηδέν, από τη σχέση Στ= προκύπτει ότι = 0 επομένως, L = σταθ. Η στροφορμή του σώματος παραμένει σταθερή.

Για παράδειγμα, κατά την περιστροφή της Γης γύρω από τον εαυτό της (ιδιοπεριστροφή), επειδή η ελκτική δύναμη που δέχεται από τον Ήλιο δε δημιουργεί ροπή, αφού ο φορέας της διέρχεται από το κέντρο μάζας της, η στροφορμή της Γης παραμένει σταθερή. Επομένως η χρονική διάρκεια περιστροφής της Γης γύρω από τον εαυτό της παραμένει σταθερή -24 ώρες.

Η διατήρηση της στροφορμής σε σύστημα σωμάτων.

0 δεύτερος νόμος του Newton για τη στροφική κίνηση στην περίπτωση συστήματος σωμάτων έχει τη μορφή Στ_εξ = . Από τη σχέση αυτή προκύπτει ότι αν το αλγεβρικό άθροισμα των ροπών των εξωτερικών δυνάμεων στο σύστημα είναι μηδέν, η στροφορμή του συστήματος διατηρείται σταθερή. Η πρόταση αυτή είναι γνωστή ως αρχή της διατήρησης της στροφορμής.

Εάν η συνολική εξωτερική ροπή σε ένα σύστημα είναι μηδέν η ολική στροφορμή του συστήματος παραμένει σταθερή.

Αν, λόγω ανακατανομής της μάζας (εξαιτίας εσωτερικών δυνάμεων), μεταβληθεί η ροπή αδράνειας ενός σώματος ως προς τον άξονα περιστροφής του, μεταβάλλεται και η γωνιακή ταχύτητά του αλλά η στροφορμή του διατηρείται σταθερή. Μπορούμε επομένως να γράψουμε:

I₁ω₁ = I₂ω₂

Τα παραδείγματα φαινομένων στα οποία διατηρείται η στροφορμή είναι πολλά. Στην εικόνα 4.4 φαίνεται μια αθλήτρια του καλλιτεχνικού πατινάζ, που στριφογυρίζει στο παγοδρόμιο. Η αθλήτρια μπορεί, συμπτύσσοντας τα χέρια και τα πόδια της, να αυξήσει τη γωνιακή ταχύτητα περιστροφής της. Εάν η τριβή των παγοπέδιλων με τον πάγο θεωρηθεί αμελητέα, οι εξωτερικές δυνάμεις - όπως το βάρος και η δύναμη που δέχεται από το έδαφος - δε δημιουργούν ροπή ως προς τον άξονα περιστροφής της, επομένως η στροφορμή της διατηρείται, δηλαδή το γινόμενο Iω παραμένει σταθερό. Συμπτύσσοντας τα χέρια και τα πόδια της η ροπή αδράνειας μειώνεται, οπότε, αφού το γινόμενο Ιω μένει σταθερό, αυξάνεται η γωνιακή ταχύτητα περιστροφής της.

Όταν οι ακροβάτες θέλουν να κάνουν πολλές στροφές στον αέρα συμπτύσσουν τα χέρια και τα πόδια τους. Κατά την κίνηση του ακροβάτη στον αέρα, μοναδική εξωτερική δύναμη είναι το βάρος του, το οποίο, επειδή διέρχεται από το κέντρο μάζας, δε δημιουργεί ροπή και η στροφορμή του διατηρείται. Με τη σύμπτυξη των άκρων μειώνεται η ροπή αδράνειας, επομένως αυξάνεται η γωνιακή ταχύτητα περιστροφής. Στο σχήμα 4.30 φαίνεται πως, με την τεχνική αυτή, μια κατάδυση μπορεί να γίνει πολύ θεαματική.

Σχ. 4.30 Με τη σύμπτυξη των άκρων μειώνεται η ροπή αδράνειας της καταδύτριας με συνέπεια την αύξηση της γωνιακής ταχύτητας περιστροφής της.

Τα αστέρια τα οποία στο τελευταίο στάδιο της ζωής τους έχουν μάζα από 1,4 έως 2,5 φορές τη μάζα του Ήλιου, μετατρέπονται σε αστέρες νετρονίων ή pulsars. Τα αστέρια αυτά, όταν εξαντλήσουν τις πηγές ενέργειας που διαθέτουν, συρρικνώνονται λόγω της βαρύτητας μέχρις ότου η πυρήνες των ατόμων τους αρχίσουν να εφάπτονται, με αποτέλεσμα η ακτίνα ενός τέτοιου αστεριού να είναι μόνο 15-20 km. Επειδή η συρρίκνωση οφείλεται σε

Εικ. 4.4 Η χορεύτρια συμπτύσσοντας τα άκρα της αυξάνει τη γωνιακή ταχύτητα περιστροφής της.

Σχ. 4.30 Με τη σύμπτυξη των άκρων μειώνεται η ροπή αδράνειας της καταδύτριας με συνέπεια την αύξηση της γωνιακής ταχύτητας περιστροφής της.

εσωτερικές δυνάμεις η στροφορμή διατηρείται σταθερή και επειδή η ροπή αδράνειας του αστεριού μειώνεται δραματικά έχουμε μια αντίστοιχη αύξηση της ταχύτητας περιστροφής. Υπολογίζεται ότι ένας αστέρας νετρονίων περιστρέφεται με συχνότητα 3000 στροφές το δευτερόλεπτο. Για σύγκριση, να αναφέρουμε ότι η περίοδος περιστροφής του Ήλιου είναι 25 μέρες.

ΠΑΡΑΔΕΙΓΜΑ 4-11

Ο άνθρωπος στο σχήμα 4.31, έχει τα χέρια του τεντωμένα και στο κάθε χέρι του κρατάει ένα βαράκι μάζας Μ= 4 kg. Εξαιτίας μιας ώθησης που δέχτηκε, ο άνθρωπος περιστρέφεται με γωνιακή ταχύτητα ω₁ = 4 rad/s. Με ποια γωνιακή ταχύτητα θα στρέφεται αν συμπτύξει τα χέρια του; Το κάθισμα πάνω στο οποίο κάθεται, ο άνθρωπος μπορεί να στρέφεται χωρίς τριβές, γύρω από κατακόρυφο άξονα, που είναι ο άξονας συμμετρίας. Η ροπή αδράνειας του ανθρώπου (χωρίς τα βαράκια που κρατάει) όταν έχει τα χέρια του τεντωμένα είναι 3,25 kgm² και όταν συμπτύσσει τα χέρια του είναι 2,5 kgm².

Σχ. 4.31

Κάθε βαράκι απέχει από τον άξονα περιστροφής 1 m, στην αρχή και 0,2 m στο τέλος. Η ροπή αδράνειας του καθίσματος είναι αμελητέα.

Απάντηση :

Η αρχική ροπή αδράνειας I₁ , του συστήματος ως προς τον άξονα περιστροφής, όταν ο άνθρωπος είχε τα χέρια του τεντωμένα, ήταν το άθροισμα της ροπής αδράνειας του ανθρώπου και της ροπής αδράνειας των σωμάτων που κρατάει.

I₁ = I₁^ανθρ + I₁^βαρ = I₁^ανθρ + 2MR₁² = 11,25 kg m²

Η ροπή αδράνειας Ι₂ του συστήματος, όταν ο άνθρωπος κατεβάσει τα χέρια του είναι η νέα ροπή αδράνειας του ανθρώπου και η ροπή αδράνειας των σωμάτων.

I₂ = I₂^ανθρ + I₂^βαρ = I₂^ανθρ + 2MR₂² = 2,82 kg m²

Επειδή στο σύστημα δεν ενεργούν εξωτερικές ροπές ως προς τον άξονα περιστροφής, η στροφορμή του διατηρείται. Δηλαδή ισχύει:

I₁ω₁ = I₂ω₂ ή ω₂ = ω₁ = 16 rad/s