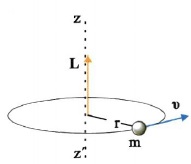
 Σχ. 4.26 Το υλικό σημείο μάζας m κινείται κυκλικά. Η στροφορμή του είναι κάθετη στο επίπεδο της τροχιάς του.
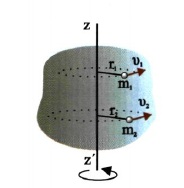 Σχ. 4.27 Το στερεό μπορεί να θεωρηθεί ότι αποτελείται από στοιχειώδη τμήματα με μάζες m1 m2 ... Κάθε μάζα εκτελεί κυκλική κίνηση γύρω από τον άξονα περιστροφής.
Σχ. 4.28 Ο κώνος του σχήματος περιστρέφεται γύρω από τον άξονα z'z με γωνιακή ταχύτητα ω. Η στροφορμή του σώματος είναι Ιω, βρίσκεται πάνω στον άξονα και η φορά της δίνεται από τον κανόνα του δεξιού χεριού.
|
4-7 ΣΤΡΟΦΟΡΜΗ
Η ορμή αποδείχτηκε μέγεθος ιδιαίτερα χρήσιμο για την περιγραφή της μεταφορικής κίνησης των στερεών. Το αντίστοιχο της ορμής του στερεού στη στροφική κίνηση το ονομάζουμε στροφορμή. Θα ορίσουμε πρώτα τη στροφορμή ενός υλικού σημείου που κάνει κυκλική κίνηση, στη συνέχεια θα ορίσουμε τη στροφορμή στερεού σώματος και, τέλος, τη στροφορμή συστήματος σωμάτων.
Έστω ένα υλικό σημείο μάζας m και ορμής ρ που κινείται σε περιφέρεια κύκλου ακτίνας r (σχ. 4.26).
L = pr ή L = mυr
Έστω το στερεό του σχήματος 4.27 που περιστρέφεται γύρω από το σταθερό άξονα z΄z με γωνιακή ταχύτητα ω. Κατά την περιστροφή του σώματος τα διάφορα σημεία του διαγράφουν κυκλικές τροχιές τα επίπεδα των οποίων είναι κάθετα στον άξονα περιστροφής. Όλα τα σημεία περιστρέφονται με την ίδια γωνιακή ταχύτητα ω, η γραμμική ταχύτητά τους όμως είναι διαφορετική, και μάλιστα ανάλογη με την απόσταση τους από τον άξονα περιστροφής. Χωρίζουμε το σώμα σε στοιχειώδη τμήματα, με μάζες m1, m2 .... , τόσο μικρά ώστε καθένα από αυτά να μπορεί να θεωρηθεί υλικό σημείο. Οι στροφορμές των στοιχειωδών αυτών μαζών έχουν όλες την ίδια κατεύθυνση και μέτρα, L1 = m1υ1r1, L2 = m2υ2r2 .... Η στροφορμή του σώματος είναι το άθροισμα των στροφορμών των υλικών σημείων που το αποτελούν. L = m1υ1r1 + m2υ2r2 +.......... Επειδή τα υλικά σημεία m1, m2 ... κάνουν κυκλική κίνηση οι ταχύτητές τους υ1,υ2 ... μπορούν να γραφούν υ1 = ωr1, υ2 = ωr2 κ. ο. κ. οπότε L = m1ωr12 + m2ωr22 +....... = ω (m1r12 + m2r22 + ........) όμως m1r12 + m2r22+..... = Ι επομένως
L = Ιω (4.17)
|
Στροφορμή μερικών σωμάτων
|
|
Ο νόμος αυτός ισχύει και σε σύστημα σωμάτων. Σε ένα σύστημα σωμάτων, το αλγεβρικό άθροισμα όλων των ροπών, δηλαδή των ροπών που οφείλονται στις εξωτερικές δυνάμεις καθώς και εκείνων που οφείλονται στις εσωτερικές δυνάμεις, είναι ίσο με το ρυθμό μεταβολής της στροφορμής του συστήματος. Η ολική ροπή των εσωτερικών δυνάμεων είναι μηδενική. Σύμφωνα με τον τρίτο νόμο του Newton οι εσωτερικές δυνάμεις απαντούν κατά ζεύγη (δράση - αντίδραση). Σε κάθε τέτοιο ζεύγος οι δυνάμεις είναι αντίθετες. Η ροπή κάθε τέτοιου ζεύγους ως προς οποιοδήποτε σημείο είναι μηδενική και επομένως το αλγεβρικό άθροισμα των ροπών όλων των εσωτερικών δυνάμεων να είναι μηδέν. Έτσι η σχέση 4.18 για σύστημα σωμάτων γράφεται Στεξ = όπου τεξ η ροπή μιας εξωτερικής δύναμης και L η στροφορμή του συστήματος. |