Φυσική Θετικών Σπουδών & Σπουδών Υγείας Γ΄ τάξη Γενικού Λυκείου (ΤΕΥΧΟΣ Γ΄)



Σχ. 4.17 Το στερεό μπορεί να θεωρηθεί ότι αποτελείται από στοιχειώδη τμήματα.
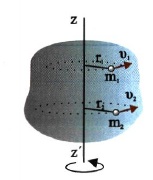
Σχ. 4.17 Το στερεό μπορεί να θεωρηθεί ότι αποτελείται από στοιχειώδη τμήματα.
4-5 ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ

Έστω ένα στερεό το οποίο στρέφεται γύρω από το σταθερό άξονα zz' (σχ.4.17). Χωρίζουμε το σώμα σε στοιχειώδη τμήματα με μάζες m1, m2 ...., τόσο μικρά ώστε καθένα από αυτά να μπορεί να θεωρηθεί υλικό σημείο. Οι μάζες m1, m2... κινούνται κυκλικά γύρω από τον άξονα, σε κύκλους ακτίνων r1,r2 ...

  1. Ονομάζουμε ροπή αδράνειας ενός στερεού ως προς κάποιο άξονα το άθροισμα των γινομένων των στοιχειωδών μαζών από τις οποίες αποτελείται το σώμα επί τα τετράγωνα των αποστάσεων τους από τον άξονα περιστροφής.

 

I = m1r12 + m2r22 +....

 

Η ροπή αδράνειας είναι μονόμετρο μέγεθος και έχει μονάδα το 1 kg m2.

Ο υπολογισμός της ροπής αδράνειας ενός σώματος συνήθως δεν είναι εύκολος.

Στον πίνακα που ακολουθεί δίνονται οι ροπές αδράνειας κάποιων σωμάτων ως προς έναν από τους άπειρους άξονες που διέρχονται από το κέντρο μάζας τους. Ο συγκεκριμένος άξονας για κάθε σώμα εικονίζεται στο σχήμα.

ΠΙΝΑΚΑΣ ΜΕ ΤΙΣ ΡΟΠΕΣ ΑΔΡΑΝΕΙΑΣ ΟΡΙΣΜΕΝΩΝ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΣΩΜΑΤΩΝ ΩΣ ΠΡΟΣ ΑΞΟΝΑ ΠΟΥ ΔΙΕΡΧΕΤΑΙ ΑΠΟ ΤΟ ΚΕΝΤΡΟ ΜΑΖΑΣ


Εικόνα

Μεταξύ της ροπής αδράνειας Icm ενός σώματος ως προς άξονα που διέρχεται από το κέντρο μάζας του και της ροπής αδράνειας Ip ως προς οποιοδήποτε άλλο άξονα ρ, παράλληλο με τον πρώτο σε απόσταση d από αυτόν, υπάρχει μια απλή σχέση, γνωστή ως το θεώρημα παραλλήλων αξόνων ή θεώρημα Steiner (Στάινερ).

  1. Αν Icm η ροπή αδράνειας ενός σώματος μάζας Μ, ως προς άξονα που διέρχεται από το κέντρο μάζας, η ροπή αδράνειάς του ως προς ένα άξονα που είναι παράλληλος και απέχει απόσταση d από τον πρώτο είναι ίση με το άθροισμα της ροπής αδράνειας ως προς τον άξονα που διέρχεται από το κέντρο μάζας του σώματος και του γινομένου της μάζας του σώματος επί το τετράγωνο της απόστασης d.

 

Ip = Icm + Md2

 Σχ. 4.18 Το θεώρημα παραλλήλων αξόνων δίνει τη ροπή αδράνειας ως προς τυχαίο άξονα που απέχει απόσταση d από το κέντρο μάζας

Σχ. 4.18 Το θεώρημα παραλλήλων αξόνων δίνει τη ροπή αδράνειας ως προς τυχαίο άξονα που απέχει απόσταση d από το κέντρο μάζας
ΠΑΡΑΔΕΙΓΜΑ 4-5

Υπολογίστε τη ροπή αδράνειας ομογενούς δακτυλίου μάζας Μ και ακτίνας R, ως προς άξονα που διέρχεται από το κέντρο του και είναι κάθετος στο επίπεδο που ορίζει. Το πάχος του δακτυλίου είναι αμελητέο σε σχέση με την ακτίνα του.

Απάντηση :


Θεωρούμε ότι ο δακτύλιος αποτελείται από τις στοιχειώδεις μάζες m1, m2....
 aaa

        Σχ. 4.19


Είναι φανερό ότι m1 + m2 + ....... = M

Επειδή το πάχος του δακτυλίου είναι αμελητέο σε σχέση με την ακτίνα του R, όλες οι στοιχειώδεις μάζες έχουν την ίδια απόσταση R από τον άξονα περιστροφής.

Σύμφωνα με τον ορισμό της ροπής αδράνειας

Ι = m1r12 + m2r22 + ...... = m1R2 + m2R2 + ..... = (m1 + m2 +.......)R2

Άρα                                        I = MR2

ΠΑΡΑΔΕΙΓΜΑ 4-6

Δυο σώματα αμελητέων διαστάσεων, με ίσες μάζες m1 και m2,(m1= m2=m),  συνδέονται μεταξύ τους με αβαρή ράβδο, μήκους l. Ποια είναι η ροπή αδράνειας του συστήματος, ως προς άξονα που είναι κάθετος στη ράβδο και διέρχεται α) από το μέσον της ράβδου β) από τη μάζα m1;

Απάντηση :
α) Ι = m1Εικόνα+ m2Εικόνα = 2m Εικόνα = Εικόνα
β) I = m1l2 + 0 = ml2

 aaa

        Σχ. 4.20
ΠΑΡΑΔΕΙΓΜΑ 4-7

Υπολογίστε τη ροπή αδράνειας ενός λεπτού ομογενούς δίσκου, μάζας Μ και ακτίνας R, ως προς άξονα που είναι κάθετος στο επίπεδο του, που περνάει από το άκρο του δίσκου.

Απάντηση :

Η ροπή αδράνειας του δίσκου ως προς άξονα που περνάει από το κέντρο μάζας του είναι

Icm = MR2/2

Εφαρμόζοντας το θεώρημα παραλλήλων αξόνων για d=R έχουμε

Ip = Icm +Md2 = Εικόνα + MR2 = Εικόνα

 aaaa

        Σχ. 4.21