Φυσική Θετικών Σπουδών & Σπουδών Υγείας Γ΄ τάξη Γενικού Λυκείου (ΤΕΥΧΟΣ Γ΄)

Σχ. 4.7 Η ίδια δύναμη περιστρέφει την πόρτα πιο εύκολα όταν ασκείται μακριά από τον άξονα περιστροφής. Η F' που ο φορέας της διέρχεται από τον άξονα δε μπορεί να περιστρέψει το σώμα.

Σχ. 4.7 Η ίδια δύναμη περιστρέφει την πόρτα πιο εύκολα όταν ασκείται μακριά από τον άξονα περιστροφής. Η F' που ο φορέας της διέρχεται από τον άξονα δε μπορεί να περιστρέψει το σώμα.Σχ. 4.8 Η φορά της ροπής της δύναμης F βρίσκεται με τον κανόνα του δεξιού χεριού.

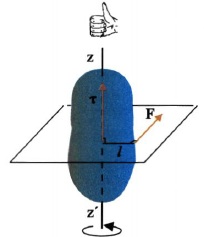Σχ. 4.8 Η φορά της ροπής της δύναμης F βρίσκεται με τον κανόνα του δεξιού χεριού.

.Σχ. 4.9 Η ροπή της δύναμης F έχει μέτρο Fx 1
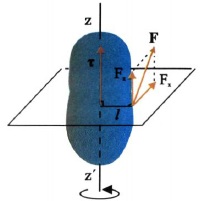Σχ. 4.9 Η ροπή της δύναμης F έχει μέτρο Fx1

4-3 ΡΟΠΗ ΔΥΝΑΜΗΣ

Αν ασκήσουμε μια δύναμη σε ένα σώμα που έχει τη δυνατότητα να στρέφεται γύρω από σταθερό άξονα το σώμα περιστρέφεται εκτός αν ο φορέας της δύναμης περνάει από τον άξονα περιστροφής. Από την εμπειρία μας γνωρίζουμε ότι η περιστροφή που προκαλεί μια δύναμη εξαρτάται όχι μόνο από την κατεύθυνση και το μέγεθος της δύναμης αλλά και από το σημείο στο οποίο ασκείται η δύναμη. Για να κλείσουμε μια πόρτα τη σπρώχνουμε κοντά στο πόμολο και όχι κοντά στον άξονα περιστροφής της (μεντεσέδες), γιατί ακόμα και μικρή δύναμη μπορεί να προκαλέσει στροφή της πόρτας όταν εφαρμόζεται μακριά από τον άξονα περιστροφής.

Το μέγεθος το οποίο περιγράφει την ικανότητα μιας δύναμης να στρέφει ένα σώμα ονομάζεται ροπή της δύναμης και συμβολίζεται με το ελληνικό τ.

Α) Ροπή δύναμης ως προς άξονα

 

Έστω ένα σώμα που έχει τη δυνατότητα να στρέφεται γύρω από τον άξονα z′z. Στο σώμα ασκείται δύναμη F που βρίσκεται σε επίπεδο κάθετο στον άξονα περιστροφής.

  1. Ροπή της δύναμης F, ως προς τον άξονα περιστροφής ονομάζεται το διανυσματικό μέγεθος που έχει μέτρο ίσο με το γινόμενο του μέτρου της δύναμης επί την κάθετη απόσταση l της δύναμης από τον άξονα περιστροφής (μοχλοβραχίονας).

 

τ = Fl


  1. Η ροπή έχει τη διεύθυνση του άξονα περιστροφής και η φορά της δίνεται από τον κανόνα του δεξιού χεριού. Μονάδα ροπής είναι το 1 Ν m.

Για να προσδιορίσουμε τη φορά της ροπής κλείνουμε τα δάχτυλα του δεξιού χεριού και τα τοποθετούμε έτσι ώστε να δείχνουν τη φορά κατά την οποία τείνει να περιστρέψει το σώμα η δύναμη. Ο αντίχειρας τότε δίνει τη φορά του διανύσματος της ροπής.

Αν η δύναμη F δε βρίσκεται σε επίπεδο κάθετο στον άξονα περιστροφής, η ροπή της είναι ίση με τη ροπή που δημιουργεί η συνιστώσα της που βρίσκεται πάνω στο κάθετο επίπεδο (σχ. 4.9)

Στο κεφάλαιο αυτό θα μελετήσουμε μόνο περιπτώσεις στις οποίες όλες οι δυνάμεις που ασκούνται στα σώματα βρίσκονται στο ίδιο επίπεδο.

Σε τέτοια προβλήματα, για να περιγράψουμε την τάση μιας δύναμης να περιστρέψει ένα σώμα προς τη μια ή την άλλη φορά, χρησιμοποιούμε την αλγεβρική τιμή της ροπής. Κατά σύμβαση θεωρούμε θετική τη ροπή της δύναμης που τείνει να περιστρέψει το σώμα αντίθετα από τη φορά των δεικτών του ρολογιού και αρνητική τη ροπή της δύναμης που τείνει να το περιστρέψει κατά τη φορά κίνησης των δεικτών του ρολογιού.

Στο σώμα του σχήματος 4.10 δρουν οι δυνάμεις F1 και F2 . Το σώμα έχει τη δυνατότητα να στρέφεται γύρω από άξονα που διέρχεται από το σημείο Ο και είναι κάθετος στο επίπεδο της σελίδας. Η συνολική ροπή που δέχεται το σώμα είναι

τ = τ1 +τ2 = F1l1 + F2l2

 

Β) Ροπή δύναμης ως προς σημείο

 

Αν σ' ένα ελεύθερο σώμα ασκηθεί δύναμη που ο φορέας της διέρχεται από το κέντρο μάζας του, το σώμα δεν περιστρέφεται (θα εκτελέσει μεταφορική κίνηση). Αν όμως ο φορέας της δύναμης δε διέρχεται από το κέντρο μάζας του, το σώμα μαζί με τη μεταφορική κίνηση θα εκτελέσει και περιστροφική γύρω από ένα νοητό άξονα (ελεύθερος άξονας) που διέρχεται από το κέντρο μάζας του σώματος και είναι κάθετος στο επίπεδο που ορίζεται από τη δύναμη και το κέντρο μάζας του σώματος.

Μπορείτε να διαπιστώσετε τα παραπάνω με ένα μολύβι που βρίσκεται πάνω σε ένα τραπέζι. Ωθώντας το μολύβι στο κέντρο μάζας του, το μολύβι κάνει μόνο μεταφορική κίνηση. Αν όμως ασκήσετε δύναμη στη μια του άκρη (ο φορέας της δεν πρέπει να διέρχεται από το κέντρο μάζας του) τότε το μολύβι στρέφεται γύρω από έναν νοητό άξονα που διέρχεται από το κέντρο μάζας του και ταυτόχρονα μετακινείται. Η μεταφορική κίνηση μπορεί να μην είναι εμφανής αν η τριβή ανάμεσα στο μολύβι και το τραπέζι είναι σημαντική .

Στις περιπτώσεις που δεν υπάρχει σταθερός άξονας περιστροφής χρησιμοποιείται η έννοια της ροπής της δύναμης ως προς σημείο.

  1. Ροπή δύναμης F ως προς σημείο Ο ονομάζουμε το διανυσματικό μέγεθος που έχει μέτρο ίσο με το γινόμενο του μέτρου της δύναμης επί την απόσταση της από το σημείο Ο

 

τ = Fl

 


  1. διεύθυνση κάθετη στο επίπεδο που ορίζεται από τη δύναμη και το σημείο Ο και φορά που δίνεται από τον κανόνα του δεξιού χεριού.

Αξιοσημείωτη είναι η περίπτωση που σε ένα σώμα δρουν δύο αντίρροπες δυνάμεις F1 και F2 με ίσα μέτρα. Δυο τέτοιες δυνάμεις αποτελούν ζεύγος δυνάμεων. Αν η απόσταση των φορέων των δυο δυνάμεων είναι d, η αλγεβρική τιμή της ροπής του ζεύγους ως προς κάποιο σημείο Α (σχ. 4.12) που απέχει απόσταση x1 από τη δύναμη F1 και x2 από την F2, είναι

τ = F1x1 + F2x2 = F (x1 + x2 ) = F1d


επομένως

 

τ = F1d

 

Το ίδιο αποτέλεσμα θα είχαμε και ως προς οποιοδήποτε άλλο σημείο. Επομένως, η ροπή ζεύγους δυνάμεων είναι ίδια ως προς οποιοδήποτε σημείο.

 

Σχ. 4.10 Στο σώμα ασκούνται οι δυνάμεις F1 και F2. Η φορά περιστροφής του σώματος καθορίζεται από το αλγεβρικό άθροισμα των ροπών.
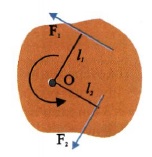Σχ. 4.10 Στο σώμα ασκούνται οι δυνάμεις F1 και F2. Η φορά περιστροφής του σώματος καθορίζεται από το αλγεβρικό άθροισμα των ροπών.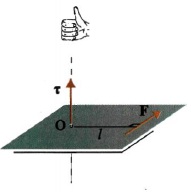

Σχ. 4.11 Προσδιορισμός της φοράς της ροπής δύναμης ως προς σημείο με τον κανόνα του δεξιού χεριού..
Σχ. 4.11 Προσδιορισμός της φοράς της ροπής δύναμης ως προς σημείο με τον κανόνα του δεξιού χεριού..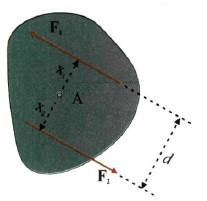

Σχ 4.12 Οι δυνάμεις F1 και F2 αποτελούν ζεύγος. Η ροπή τους είναι ίδια ως προς οποιοδήποτε σημείο του επιπέδου τους.
Σχ 4.12 Οι δυνάμεις F1 και F2 αποτελούν ζεύγος. Η ροπή τους είναι ίδια ως προς οποιοδήποτε σημείο του επιπέδου τους.
ΠΑΡΑΔΕΙΓΜΑ 4-1

Το στερεό του σχήματος 4.13 αποτελείται από δύο ομοαξονικούς κυλίνδρους, με ακτίνες R1=4 cm και R2=3 cm, που στέφονται γύρω από σταθερό άξονα x’x. Ο άξονας x’x συμπίπτει με τον άξονα συμμετρίας των κυλίνδρων. Εξ αιτίας των βαρών που κρέμονται από τους δύο κυλίνδρους, τα σκοινιά ασκούν στους κυλίνδρους δυνάμεις F1=6 Ν και F2=10 Ν. Να υπολογίσετε την ολική ροπή που δέχεται το στερεό.
Σχ.4.13

                                     Σχ.4.13

 

Απάντηση:
Η δύναμη F1 τείνει να στρέψει το στερεό κατά τη θετική φορά και δημιουργεί θετική ροπή τ1 = F1R1
Η δύναμη F2 τείνει να το στρέψει κατά την αρνητική φορά και δημιουργεί ροπή τ2 =- F2R2
Η συνολική ροπή που δέχεται το στερεό είναι τ = τ1+τ2 = F1R1 - F2R2 = -0,06 Νm

Το αρνητικό πρόσημο δείχνει ότι το στερεό θα στραφεί όπως στρέφονται οι δείκτες του ρολογιού.

ΠΑΡΑΔΕΙΓΜΑ 4-2

 

Η αβαρής ράβδος του σχήματος 4.14 μπορεί να στρέφεται γύρω από άξονα που διέρχεται από το σημείο Ο και είναι κάθετος σε αυτή. Το Ο απέχει από τα άκρα της ράβδου x1=5 cm και x2=8 cm. Στα άκρα της ράβδου ασκούνται οι δυνάμεις F1=50 Ν και F2=40 Ν. Η δύναμη F2 σχηματίζει γωνία φ= 30° με τη ράβδο. Πόση είναι η ολική ροπή που δέχεται η ράβδος;

 Σχ.4.14

             Σχ.4.14

 

Απάντηση :

Η ροπή της F1 είναι θετική γιατί η δύναμη τείνει να στρέψει τη ράβδο κατά τη θετική φορά. Είναι

τ1 = F1x1 = 2,5 N

Για να υπολογίσουμε τη ροπή της F2 την αναλύουμε στις συνιστώσες F2x και F2y με μέτρα F2x = F2συν30ο και F2y=F2ημ30ο. Η ροπή της F2x είναι μηδέν διότι ο φορέας της διέρχεται από τον άξονα ( η απόσταση της F2x από τον άξονα είναι μηδέν), ενώ η ροπή της F2y είναι αρνητική και ίση με

τ2 = - F2ημ30οx2 = -1,6 Nm

Η συνολική ροπή που δέχεται η ράβδος είναι

τ = τ1+τ2 = 0,9Nm

Η συνολική ροπή είναι θετική, επομένως η ράβδος θα στραφεί αντίθετα με τη φορά της κίνησης των δεικτών του ρολογιού