| ένα κάτω από το άλλο με μία μετατόπιση από τα δεξιά προς τα αριστερά καθώς θεωρούμε διαδοχικά τα ψηφία των μονάδων, των δεκάδων, των εκατοντάδων κ.λπ. Στη συνέχεια γίνεται η πρόσθεση των επιμέρους γινομένων, αφού τα τοποθετήσουμε στην κατάλληλη διάταξη όπως φαίνεται στο σχήμα 2.7. Ωστόσο, η πράξη του πολλαπλασιασμού δεν εκτελείται από τον υπολογιστή με τον τρόπο αυτό. Πιο συγκεκριμένα, ο χρησιμοποιούμενος τρόπος είναι ο λεγόμενος πολλαπλασιασμός αλά ρωσικά. Χωρίς βλάβη της γενικότητας θεωρούμε ότι οι ακέραιοι είναι θετικοί (μεγαλύτεροι του μηδενός), αλλά η μέθοδος μπορεί εύκολα να μετατραπεί, ώστε να περιγράψει και την περίπτωση των αρνητικών ακεραίων. Πώς ακριβώς λειτουργεί η μέθοδος, θα φανεί με το επόμενο παράδειγμα, όπου περιγράφεται ο αλγόριθμος με ελεύθερο κείμενο. Έστω, λοιπόν, ότι δίνονται δύο θετικοί ακέραιοι αριθμοί, οι αριθμοί 45 και 19. Οι αριθμοί γράφονται δίπλα-δίπλα και ο πρώτος διπλασιάζεται, ενώ ο δεύτερος υποδιπλασιάζεται αγνοώντας το δεκαδικό μέρος. Στο σχήμα 2.8 παρουσιάζεται η επαναλαμβανόμενη διαδικασία, που συνεχίζεται μέχρις ότου στη δεύτερη στήλη να προκύψει μονάδα. Τελικώς, το γινόμενο ισούται με το άθροισμα των στοιχείων της πρώτης στήλης, όπου αντίστοιχα στη δεύτερη στήλη υπάρχει περιττός αριθμός. Για το παράδειγμά μας, τα στοιχεία αυτά παρουσιάζονται στην τρίτη στήλη. Ολίσθηση (shift) Στα κυκλώματα του υπολογιστή τα δεδομένα αποθηκεύονται με δυαδική μορφή, δηλαδή 0 και 1, ανεξάρτητα από το πως τα ορίζει ο προγραμματιστής, όπως ακεραίους ή πραγματικούς σε δεκαδικό σύστημα, ή ακόμη χαρακτήρες κ.λπ. Έτσι ο αριθμός 17 του δεκαδικού συστήματος ισοδυναμεί με τον αριθμό 00010001 του δυαδικού συστήματος, ο οποίος μπορεί να αποθηκευθεί σε ένα byte. Αν μετακινήσουμε τα ψηφία αυτά κατά μία θέση προς τα αριστερά, δηλαδή αν προσθέσουμε ένα 0 στο τέλος του αριθμού και αγνοήσουμε το αρχικό 0, τότε προκύπτει ο αριθμός 00100010 του δυαδικού συστήματος, που ισοδυναμεί με το αριθμό 34 του δεκαδικού συστήματος. Επίσης, με παρόμοιο τρόπο, αν μετακινήσουμε τα ψηφία κατά μία θέση δεξιά, δηλαδή αποκόψουμε το τελευταίο ψηφίο 1 και θεωρήσουμε ένα ακόμη αρχικό 0, τότε προκύπτει ο αριθμός 00001000 του δυαδικού συστήματος, που ισοδυναμεί με τον αριθμό 8 του δεκαδικού συστήματος. Άρα η ολίσθηση προς τα αριστερά ισοδυναμεί με πολλαπλασιασμό επί δύο, ενώ η ολίσθηση προς τα δεξιά ισοδυναμεί με την ακέραια διαίρεση διά δύο. | 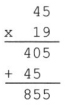 Σχ. 2.7. Χειρωνακτικός τρόπος πολλαπλασιασμού.
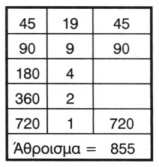 Σχ. 2.8. Πολλαπλασιασμός αλά ρωσικά. |
