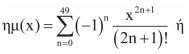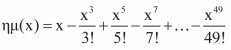2.2 Αλγόριθμοι

Αλγόριθμοι

Στόχοι του κεφαλαίου αυτού είναι να μπορούν οι μαθητές:

να περιγράφουν την έννοια του αλγορίθμου και να διακρίνουν την ύπαρξη συγκεκριμένων χαρακτηριστικών που χρειάζεται να έχει ένας αλγόριθμος
να αναγνωρίζουν βασικές έννοιες στην Ανάλυση Αλγορίθμων
να αναγνωρίζουν τις διάφοΣχεσιακοί τελεστέςρες μορφές αναπαράστασης αλγορίθμου
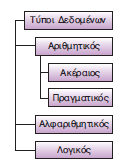
να αναφέρουν τους βασικούς τύπους και δομές δεδομένων
να διακρίνουν τις βασικές εντολές και δομές που χρησιμοποιούνται σε έναν αλγόριθμο
να προσδιορίζουν τον τρόπο λειτουργίας των δομών δεδομένων
να εκπονούν απλούς αλγορίθμους
να εντοπίζουν και να διορθώνουν τα λογικά λάθη ενός αλγορίθμου
να εξηγούν την ανάγκη δημιουργίας της κατάλληλης τεκμηρίωσης.

2.2.1 Ορισμός αλγορίθμου

Η λέξη αλγόριθμος (algorithm) προέρχεται από μια μελέτη του Πέρση μαθηματικού Μοχάμεντ Ιμπν Μουσά Αλ Χουαρίζμι (Muhammad ibn Mūsā al-Khwārizmī), που έζησε περί το 825 μ.Χ. (Εικόνα 2.8). Παρόλα αυτά, η ύπαρξη και η ηλικία μερικών αλγορίθμων αριθμεί χιλιάδες χρόνια. Σήμερα, το πεδίο της μελέτης των αλγορίθμων (το οποίο καλείται θεωρία αλγορίθμων) είναι ένα ιδιαίτερα ευρύ πεδίο έρευνας. Γενικά,

Αλγόριθμος είναι μια πεπερασμένη σειρά ενεργειών, αυστηρά καθορισμένων και εκτελέσιμων σε πεπερασμένο χρόνο, που στοχεύουν στην επίλυση ενός προβλήματος.

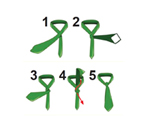
Η έννοια του αλγορίθμου δεν συνδέεται αποκλειστικά και μόνο με προβλήματα της Πληροφορικής. Για παράδειγμα, το δέσιμο της γραβάτας αποτελεί ένα πρόβλημα, για την επίλυση του οποίου χρειάζεται να εκτελεστεί μια πεπερασμένη σειρά ενεργειών (Εικόνα 2.9.). Η αλληλουχία των ενεργειών οδηγεί στο επιθυμητό αποτέλεσμα. Η αλληλουχία δεν είναι απαραίτητα μοναδική για την επίτευξη αυτού του, αφού, υπάρχουν και άλλοι τρόποι για το δέσιμο της γραβάτας.

2.2

ΚΕΦΑΛΑΙΟ

Προερωτήσεις

Ξέρεις ότι ήδη έχεις χρησιμοποιήσει πολλούς αλγορίθμους;
Μπορείς να περιγράψεις πώς βρίσκεις το Μέγιστο Κοινό Διαιρέτη δύο αριθμών;
Τι κάνεις για να εντοπίσεις μία λέξη σε ένα λεξικό;

Εικόνα 2.8. Ο Αλ Χουαρίζμι

Η μελέτη του Αλ Χουαρίζμι μεταφράστηκε στα λατινικά και άρχιζε με τη φράση «Algoritmi dixit...» (ο αλγόριθμος λέει ....).

Εικόνα 2.9. Αλγόριθμος δεσίματος γραβάτας

Ο όρος αλγόριθμος επέζησε επί χίλια χρόνια ως σπάνιος όρος, που σήμαινε κάτι σαν «συστηματική διαδικασία αριθμητικών χειρισμών». Τη σημερινή του αξία απόκτησε στις αρχές του 20ού αιώνα με την ανάπτυξη της θεωρίας αλγορίθμων και φυσικά με τους υπολογιστές.

Ιστορικά, ένας από τους πρώτους αλγορίθμους, είναι ο αλγόριθμος για την εύρεση του Μέγιστου Κοινού Διαιρέτη (ΜΚΔ) δύο ακεραίων αριθμών x και y.

Παράδειγμα 2.4. Να βρεθεί ο Μέγιστος Κοινός Διαιρέτης (ΜΚΔ) δύο θετικών ακεραίων αριθμών x και y.

Απάντηση

Ο αλγόριθμος περιγράφεται σε ομιλούμενη γλώσσα ως εξής: Θέσε στο z τον διαιρέτη. Αν z = 0, τότε ΜΚΔ είναι ο x. Αν z ≠ 0 τότε διαίρεσε το x με το y, και έστω z το υπόλοιπο και επανάλαβε τη διαίρεση με τους ακέραιους y και z αντί για x και y μέχρι το z να γίνει 0.

Για παράδειγμα προκειμένου να βρεθεί ο ΜΚΔ δύο μη μηδενικών αριθμών, π.χ. των 78 και 27, σύμφωνα με τον αλγόριθμο μπορείτε να κάνετε τις ακόλουθες ενέργειες:

Βρείτε το υπόλοιπο της διαίρεσης του 78 με το 27. Το υπόλοιπο είναι 24.

Ελέγξτε αν είναι 0. Στην περίπτωση αυτή δεν είναι 0. Αφού δεν είναι 0, βρείτε το υπόλοιπο της διαίρεσης του 27 με το 24. Το υπόλοιπο είναι 3.

Ελέγξτε αν είναι 0. Στην περίπτωση αυτή δεν είναι 0. Αφού δεν είναι 0, βρείτε το υπόλοιπο της διαίρεσης του 24 με το 3. Το υπόλοιπο είναι 0. Αφού το υπόλοιπο είναι 0, βρέθηκε ο ΜΚΔ. Ο ΜΚΔ είναι 3.

Ο αλγόριθμος αυτός μπορεί να εκφραστεί και με κωδικοποιημένο τρόπο ως εξής:

Αλγόριθμος Ευκλείδης
Διάβασε x, y
z ← y
Όσο z ≠ 0 επανάλαβε
z ← x mod y
x ← y
y ← z
Τέλος_επανάληψης
Εμφάνισε x
Τέλος Ευκλείδης

Για την περιγραφή του αλγορίθμου χρησιμοποιείται μια γλώσσα στην οποία το όνομα του αλγορίθμου (Ευκλείδης) καθορίζει την αρχή και το τέλος του.

Οι τιμές εισόδου (x, y) δίνονται με την εντολή Διάβασε, ενώ ο ΜΚΔ είναι η τιμή που παίρνει τελικά η μεταβλητή x, η οποία εμφανίζεται.

Η εύρεση του ΜΚΔ είναι μια επαναληπτική διαδικασία που συνεχίζεται όσο το υπόλοιπο (mod) της διαίρεσης x διά του y είναι διάφορο του μηδενός. Η επαναληπτική διαδικασία έχει την έννοια «όσο ισχύει η συνθήκη (δηλαδή όσο z ≠ 0) επαναλάμβανε τη διαδικασία, αλλιώς μην εκτελείς άλλο τη διαδικασία και συνέχισε στο επόμενο βήμα». Οι εντολές του τύπου x ← y δεν έχουν την έννοια της ισότητας, αλλά της εκχώρησης τιμής του δεξιού μέλους στη μεταβλητή του αριστερού μέλους. Αυτό σημαίνει ότι μετά την εκτέλεση της εντολής η μεταβλητή του αριστερού μέλους θα έχει τιμή ίση με αυτή του δεξιού μέλους.

2η

ENOTHTA

Θέματα Θεωρητικής
Επιστήμης των Υπολογιστών

«Ο ευκλείδειος αλγόριθμος είναι ο παππούς όλων των αλγορίθμων, αφού είναι ο παλαιότερος μη τετριμμένος αλγόριθμος που χρησιμοποιείται ακόμα και σήμερα.»
(Ντόναλντ Κνουθ, Donald Knuth, 1981)

Στον ευκλείδειο αλγόριθμο, δεν έχει σημασία αν θα είναι η τιμή του y μικρότερη από την τιμή του x. Έτσι, στην αρχική εκτέλεση του αλγορίθμου έχει επιλεγεί ο πρώτος αριθμός να είναι μεγαλύτερος του δευτέρου. Στη συνέχεια θα εκτελεστεί ο αλγόριθμος με τους ίδιους αριθμούς, όπου ο πρώτος αριθμός θα είναι μικρότερος του δευτέρου.

Απαραίτητο είναι οι τιμές των δύο μεταβλητών να είναι ακέραιες και μία εκ των δύο μεταβλητών να είναι διάφορη του μηδενός. Στην περίπτωση αρνητικών τιμών ο ΜΚΔ προκύπτει από τη μελέτη των απολύτων τιμών των δύο αριθμών.

Η εκτέλεση του ευκλείδειου αλγορίθμου, μπορεί να πραγματοποιηθεί από κάποιον που δεν χρειάζεται απαραίτητα να έχει κατασκευάσει τον αλγόριθμο. Επιπλέον, ο αλγόριθμος εφόσον κωδικοποιηθεί σε γλώσσα προγραμματισμού, μπορεί να εκτελεστεί από τον υπολογιστή.

Με βάση τα παραπάνω, ο ευκλείδειος αλγόριθμος για τον υπολογισμό του ΜΚΔ δύο θετικών ακεραίων αριθμώ ν, περιγράφεται πλήρως με ακρίβεια και σαφήνεια. Συνεπώς, αν το ζητούμενο είναι να υπολογιστεί με τη χρήση του αλγόριθμου Ευκλείδης, ο ΜΚΔ των αριθμών 27 και 78, τότε θα μπορούσε να αξιοποιηθεί η αρίθμηση των γραμμών του αλγορίθμου και να πραγματοποιηθεί εκτέλεσή του στο χαρτί. Σε κάθε επανάληψη υπολογίζονται οι τιμές των x, y και z, οι οποίες παρουσιάζονται στον πίνακα 2.1. Με την ολοκλήρωση προκύπτει ότι ο ΜΚΔ των αριθμών 27 και 78 είναι ο αριθμός 3.

**Πίνακας 2.1.** Εικονική εκτέλεση του
ευκλείδειου αλγορίθμου
Αριθμός εντολής	x	y	z	z ≠ 0	Έξοδος
2	27	78
3			78
4				Αληθής
5			27
6	78
7		27
4				Αληθής
5			24
6	27
7		24
4				Αληθής
5			3
6	24
7		3
4				Αληθής
5			0
6	3
7		0
4				Ψευδής
9					3

Ο παραπάνω αλγόριθμος, μπορεί να απαντήσει όχι μόνο στη συγκεκριμένη ερώτηση, «να βρεθεί ο ΜΚΔ των 27 και 78», αλλά σε όλες τις παρόμοιες ερωτήσεις. Λύνει, δηλαδή, ένα πρόβλημα. Κάθε μία από τις ερωτήσεις αυτές λέγεται στιγμιότυπο του προβλήματος. Έτσι, η εύρεση του ΜΚΔ των 27 και 78 είναι ένα στιγμιότυπο του προβλήματος της εύρεσης του ΜΚΔ δύο θετικών ακεραίων. Δηλαδή, αν εκτελεστούν τα βήματα του αλγορίθμου, θα ολοκληρωθεί η διαδικασία έχοντας πάρει τη σωστή απάντηση για οποιοδήποτε ζευγάρι θετικών ακεραίων.

Ωστόσο, ένα θεωρητικό ερώτημα που προκύπτει είναι το ακόλουθο: «γιατί ο αλγόριθμος λύνει οποιοδήποτε στιγμιότυπο του προβλήματος;» Συνήθως, για να λύνει πραγματικά ο αλγόριθμος ένα πρόβλημα, χρειάζεται να μπορεί να αποδειχτεί η ορθότητά του με αυστηρό τρόπο. Στην περίπτωση του ευκλείδειου αλγορίθμου, αποδεικνύεται από τον ίδιο τον Ευκλείδη στο έβδομο βιβλίο των «Στοιχείων» του.

2.2

ΚΕΦΑΛΑΙΟ

Αλγόριθμοι

Η εκτέλεση ενός αλγορίθμου πραγματοποιείται αφού αριθμηθούν οι γραμμές του αλγορίθμου. Για κάθε εντολή που εκτελείται, καταγράφετε τον αριθμό της γραμμής και το αποτέλεσμα της εκτέλεσης στο αντίστοιχο κελί.

Η αρίθμηση των γραμμών του αλγορίθμου είναι απαραίτητη μόνο για την εκτέλεσή του.

Οι εντολές της γραμμής 1 και 10 είναι δηλωτικές εντολές και δεν αποτυπώνονται στον πίνακα 2.1.

Ο Ευκλείδης έζησε περίπου από το 330 έως το 275 π.Χ. και έγραψε το έργο «Τα Στοιχεία» που αποτελείται από 13 βιβλία, τα οποία επιχειρούν να συστηματοποιήσουν τις μαθηματικές γνώσεις της εποχής του.

Ο ευκλείδειος αλγόριθμος έχει πολλές θεωρητικές και πρακτικές εφαρμογές. Μέσω αυτού μπορούν να δημιουργηθούν αρκετοί παραδοσιακοί μουσικοί ρυθμοί. Χρησιμοποιείται στην κρυπτογραφία, στο ηλεκτρονικό εμπόριο, στην επίλυση διοφαντικών εξισώσεων κ.α.

2.2.2 Χαρακτηριστικά αλγορίθμου

Κάθε αλγόριθμος είναι σημαντικό να έχει ορισμένα χαρακτηριστικά προκείμενου να θεωρείται πλήρης.

Καθοριστικότητα: Κάθε εντολή ενός αλγορίθμου χρειάζεται να καθορίζεται χωρίς καμία αμφιβολία για τον τρόπο εκτέλεσής της.

Κατά τη διαίρεση δύο ακεραίων αριθμών, το χαρακτηριστικό της καθοριστικότητας ικανοποιείται αν έχει ληφθεί υπόψη και η περίπτωση που ο διαιρέτης είναι μηδέν.

Περατότητα: Κάθε αλγόριθμος πρέπει να τελειώνει μετά από πεπερασμένα βήματα εκτέλεσης των εντολών του.

Ένας αλγόριθμος για να διαθέτει το χαρακτηριστικό της περατότητας, χρειάζεται να προσδιορίζει τη λύση ενός προβλήματος μετά από ένα συγκεκριμένο αριθμό βημάτων και να μην εκτελείται ατέρμονα (δηλαδή χωρίς να τελειώνει).

Αποτελεσματικότητα: Κάθε εντολή ενός αλγορίθμου χρειάζεται να είναι διατυπωμένη απλά και κατανοητά, ώστε να μπορεί να εκτελεστεί επακριβώς και σε πεπερασμένο μήκος χρόνου.

Κατά τη διαίρεση δύο ακέραιων αριθμών, ο αλγόριθμος διαθέτει το χαρακτηριστικό της αποτελεσματικότητας, αφού οι ακέραιοι αναπαρίστανται ακριβώς και υπάρχει αλγόριθμος για τη διαίρεσή τους (Ευκλείδεια Διαίρεση) σε πεπερασμένο χρόνο. Αν όμως επιχειρείται η διαίρεση δύο πραγματικών αριθμών που ο καθένας αναπαρίσταται από άπειρα δεκαδικά ψηφία, τότε ο αλγόριθμος δεν διαθέτει το χαρακτηριστικό της αποτελεσματικότητας, αφού δεν μπορεί να αναπαρασταθεί πλήρως και να εκτελεστεί ακριβώς η συγκεκριμένη διαίρεση.

Είσοδος: Κάθε αλγόριθμος χρειάζεται να δέχεται ένα σύνολο μεταβλητών εισόδου (που μπορεί να είναι και το κενό σύνολο), οι οποίες αποτελούν τα δεδομένα του αλγορίθμου.

Η είσοδος των μεταβλητών μπορεί να επιτευχθεί με κατάλληλες εντολές, οι οποίες θα παρουσιαστούν σε επόμενες παραγράφους. Στην περίπτωση του αλγόριθμου Ευκλείδης που παρουσιάστηκε στο παράδειγμα 2.4, αυτό επιτυγχάνεται με την εντολή Διάβασε x, y.

2η

ENOTHTA

Θέματα Θεωρητικής
Επιστήμης των Υπολογιστών

Χαρακτηριστικά ενός αλγορίθμου

Καθοριστικότητα (Definiteness)
Περατότητα (Finiteness)
Αποτελεσματικότητα (Effectiveness)
Είσοδος (Input)
Έξοδος (Output)

Όπως θα παρουσιαστεί σε επόμενη παράγραφο, η είσοδος σε ένα αλγόριθμο μπορεί να επιτευχθεί με την εντολή Διάβασε, την εντολή Δεδομένα και την εντολή εκχώρησης. Με την εντολή εκχώρησης δημιουργούνται δεδομένα μέσα στον αλγόριθμο (κενό σύνολο μεταβλητών εισόδου).

Έξοδος: Κάθε αλγόριθμος χρειάζεται να δημιουργεί κάποιο αποτέλεσμα.

Το αποτέλεσμα του αλγορίθμου, η έξοδός του, είναι μία ή περισσότερες μεταβλητές ή/και σταθερές τιμές. Η έξοδος μπορεί να επιτευχθεί με κατάλληλες εντολές, οι οποίες θα παρουσιαστούν σε επόμενες παραγράφους. Στην περίπτωση του αλγόριθμου Ευκλείδης που παρουσιάστηκε στο παράδειγμα 2.4, αυτό επιτυγχάνεται με την εντολή Εμφάνισε x.

2.2.3 Ανάλυση Αλγορίθμων, Θεωρία Υπολογισμού, Πολυπλοκότητα Αλγορίθμων, Υπολογισιμότητα Αλγορίθμων.

Η ανάλυση της συμπεριφοράς ενός αλγορίθμου για συνθήκες παρόμοιες με αυτές που εμφαίζονται στην πράξη και η ικανοποιητική απόδοσή του, παρέχει τη δυνατότητα να πραγματοποιηθεί η υλοποίηση και η εφαρμογή του. Αν δεν επιτυγχάνεται ικανοποιητική απόδοση τότε απαιτείται ο σχεδιασμός ενός τροποποιημένου αλγορίθμου.

Η Θεωρία Υπολογισμού (Theory of computation) είναι το πεδίο της πληροφορικής που ασχολείται τόσο με το πρόβλημα ύπαρξης λύσης ενός προβλήματος όσο και αποδοτικότητας των αλγορίθμων για την επίλυση των προβλημάτων με βάση ένα δεδομένο μοντέλο υπολογισμού.

Το πεδίο της θεωρίας υπολογισμού, διαιρείται σε δύο κλάδους: τη Θεωρία Υπολογισιμότητας (Computability Theory) και τη Θεωρία Πολυπλοκότητας (Computational Complexity Theory). Συνεπώς, για κάθε αλγόριθμο απαιτείται ανάλυση, μέσω της οποίας:

α) τεκμηριώνεται η ορθότητά του, δηλαδή αν ο αλγόριθμος κάνει πραγματικά τη δουλειά για την οποία έχει σχεδιαστεί και

β) μετριέται ποσοτικά η απόδοσή του, σε σχέση με διάφορα είδη υπολογιστικών πόρων, όπως είναι ο χρόνος και η μνήμη που απαιτείται για την εκτέλεσή του.

Η ανάλυση ενός αλγορίθμου είναι η εκτίμηση του πλήθους των υπολογιστικών πόρων που απαιτεί η εκτέλεση του αλγορίθμου.

Για παράδειγμα, ο αλγόριθμος Ευκλείδης χρησιμοποιεί τόση μνήμη όση χρειάζεται για να αποθηκευτούν οι τρεις ακέραιοι x, y, z. Ωστόσο, η εύρεση του πλήθους των εντολών που εκτελούνται δεν είναι τόσο τετριμμένη. Κάθε φορά που πραγματοποιείται η επανάληψη εκτελούνται τέσσερα βήματα (έλεγχος της συνθήκης Όσο...επανάλαβε, υπολογισμός του z και δύο εντολές εκχώρησης). Επομένως, απαιτούνται 4×α βήματα, όπου α είναι ο αριθμός των επαναλήψεων. Πόσες, όμως, θα είναι οι επαναλήψεις;

2.2

ΚΕΦΑΛΑΙΟ

Αλγόριθμοι

Η πιο συνηθισμένη ανάλυση ενός αλγορίθμου αφορά το χρόνο εκτέλεσης. Ο χρόνος συνήθως υπολογίζεται σαν συνάρτηση του αριθμού των στοιχειωδών βημάτων που εκτελούνται στον αλγόριθμο.

Η Θεωρία Υπολογισιμότητας ερευνά αν και πόσο αποδοτικά κάποια προβλήματα μπορούν να επιλυθούν με συγκεκριμένα υπολογιστικά μοντέλα.

Η Θεωρία Πολυπλοκότητας μελετά τους πόρους που απαιτούνται για την επίλυση ενός προβλήματος βάσει ενός συγκεκριμένου αλγορίθμου.

Το ότι για x = 27 και y = 78 γίνονται τέσσερις επαναλήψεις, δεν είναι πολύ διαφωτιστικό. Θα ήταν χρήσιμο να μπορεί να υπολογιστεί ο αριθμός των επαναλήψεων για κάθε ζευγάρι ακεραίων x, y.

Έχει υπολογιστεί, ότι ο αριθμός των επαναλήψεων είναι περίπου ίσος με τον λογάριθμο του x (ή του y). Δηλαδή, ο ευκλείδειος αλγόριθμος για να υπολογίσει το ΜΚΔ των x και y, κάνει 4×logx βήματα. Συνήθως παραλείπονται σταθερές, όπως το 4 και έτσι προκύπτει ότι η πολυπλοκότητα του αλγόριθμου είναι O(logx) (διαβάζεται «η πολυπλοκότητα του αλγορίθμου είναι της τάξης logx»).

Η πολυπλοκότητα ενός αλγορίθμου δίνει ένα μέτρο της χρονικής καθυστέρησης του αλγορίθμου για την επίλυση ενός προβλήματος.

Οι περισσότεροι αλγόριθμοι έχουν πολυπλοκότητα χρόνου που ανήκει σε μια από τις κατηγορίες που φαίνονται στον Πίνακα 2.2. Με n συμβολίζεται το μέγεθος του προβλήματος και εξαρτάται από το πρόβλημα. Για παράδειγμα, αν ζητείται να ταξινομηθούν k αριθμοί, τότε το μέγεθος του προβλήματος είναι k, επομένως n = k.

**Πίνακας 2.2:** Κατηγορίες πολυπλοκότητας αλγορίθμων
Πολυπλοκότητα	Ονομασία	Παρατηρήσεις
Ο(1)	Σταθερή	Κάθε βήμα εκτελείται μια φορά ή το πολύ μερικές φορές
Ο(logn)	Λογαριθμική	Αν δεν σημειώνεται αλλιώς, οι λογάριθμοι είναι δυαδικοί (Δυαδική Αναζήτηση)
Ο(n)	Γραμμική	Σειριακή αναζήτηση
Ο(nlogn)		Γρήγορη Ταξινόμηση
Ο(n2)	Τετραγωνική	Ταξινόμηση με επιλογή
O(n3)	Κυβική	Πολλαπλασιασμός πινάκων
Ο(2n)	Εκθετική	Μερισμός συνόλου

Στην εικόνα 2.10 έχουν παρασταθεί οι καμπύλες των κυριότερων συναρτήσεων πολυπλοκότητας, ενώ στον Πίνακα 2.3 παρουσιάζονται οι χρόνοι εκτέλεσης για διάφορες πολυπλοκότητες και μεγέθη προβλημάτων.

Εικόνα 2.10: Καμπύλες των κυριότερων συναρτήσεων πολυπλοκότητας.

2η

ENOTHTA

Θέματα Θεωρητικής
Επιστήμης των Υπολογιστών

Ο Lame απέδειξε ότι ο αριθμός των βημάτων του ευκλείδειου αλγορίθμου για δύο αριθμούς είναι πάντα μικρότερος ή ίσος του πενταπλασίου των ψηφίων του μεγαλύτερου από τους δύο αριθμούς.

s ≥ 4,785×log10n + 1,6723

O συμβολισμός Ο (O-notation), όπου το Ο είναι το αρχικό γράμμα της αγγλικής λέξης order και διαβάζεται «όμικρον κεφαλαίο», χρησιμοποιείται για να αναδείξει τη γενική συμπεριφορά (την τάξη) του αλγορίθμου.

Υπολογισιμότητα:

Τι μπορεί να υπολογιστεί;
Μπορεί ένας υπολογιστής να λύσει οποιοδήποτε πρόβλημα δοθέντος αρκετού χρόνου και χώρου;

Πολυπλοκότητα

Πόσο γρήγορα μπορεί να λυθεί ένα πρόβλημα;
Πόσος χώρος (μνήμη) χρειάζεται για να λυθεί ένα πρόβλημα;

Γενικά, τα δεδομένα συνιστούν το μέγεθος της εισόδου ενός αλγορίθμου. Για παράδειγμα στην ταξινόμηση, το πλήθος των αντικειμένων που θα ταξινομηθούν δίνει το μέγεθος του προβλήματος.

**Πίνακας 2.3.** Χρόνοι εκτέλεσης για διάφορες πολυπλοκότητες και μεγέθη προβλημάτων
Τάξη αλγορίθμου	Μέγεθος Προβλήματος
Τάξη αλγορίθμου	4	16	64
Ο(logn)	6×10-10 sec	1,6×10-8	1,8×10-8
O(nlogn)	2×10-8 sec	19×10-8	1,2×10-6
O(n)	4×10-8 sec	16×10-8	64×10-8
O(n2)	2×10-8 sec	2,6×10-6	4×10-5
O(n3)	64×10-8 sec	4×10-5	3×10-3
O(2n)	16×10-8 sec	65×10-5	5×103 χρόνια
O(n!)	24×10-8 sec	58 ώρες	4×1073 χρόνια

Μετά την επίλυση ενός προβλήματος με ένα αλγόριθμο γίνεται προσπάθεια να σχεδιαστεί ένας νέος αλγόριθμος με μεγαλύτερη ταχύτητα εύρεσης της λύσης του προβλήματος. Για παράδειγμα ένας αλγόριθμος ταξινόμησης με συγκρίσεις (ο οποίος περιγράφεται σε επόμενο κεφάλαιο) απαιτεί Ο(n2) συγκρίσεις. Υπάρχουν όμως ταχύτεροι αλγόριθμοι, όπως ο αλγόριθμος γρήγορης ταξινόμησης (Quicksort), που απαιτεί Ο(nlogn) συγκρίσεις.

Η μελέτη αυτού του ζητήματος γίνεται στο πλαίσιο της Θεωρίας Πολυπλοκότητας. Η έρευνα στην περιοχή αυτή προσπαθεί να βρει τους εγγενείς περιορισμούς στην ταχύτητα των αλγορίθμων για τη λύση συγκεκριμένων προβλημάτων. Έτσι αποδεικνύεται, για παράδειγμα, ότι δεν είναι δυνατόν να ταξινομηθούν n ακέραιοι με λιγότερο από nlοgn συγκρίσεις και συνεπώς ο αλγόριθμος γρήγορης ταξινόμησης είναι ουσιαστικά βέλτιστος, όσον αφορά την ταχύτητα ταξινόμησης.

2.2.4 Βασικοί τύποι αλγορίθμων

Ο ορισμός του αλγορίθμου που δόθηκε στην αρχή αυτού του κεφαλαίου, συμφωνεί με τη φιλοσοφία των περισσότερων υπολογιστών σήμερα, που διαθέτουν μία Κεντρική Μονάδα Επεξεργασίας (ΚΜΕ) στην οποία οι εντολές εκτελούνται με σειρά, η μία μετά την άλλη. Για το λόγο αυτό ονομάζονται σειριακοί αλγόριθμοι. Όμως η ύπαρξη προβλημάτων στα οποία απαιτείται πολύ μεγάλος χρόνος για τον υπολογισμό της λύσης ενός προβλήματος, δημιούργησε την ανάγκη εύρεσης αλγορίθμων, όπου ορισμένα ή μία σειρά από βήματα αυτών των αλγορίθμων θα μπορούσαν να εκτελούνται παράλληλα (ταυτόχρονα). Σε αυτή την περίπτωση, η εκτέλεση του ενός βήματος δεν εξαρτάται από την ολοκλήρωση της εκτέλεσης του προηγούμενου. Αλγόριθμοι αυτής της μορφής ονομάζονται παράλληλοι αλγόριθμοι και η υλοποίησή τους γίνεται με την ύπαρξη πολλαπλών ΚΜΕ στο σύστημα του υπολογιστή.

2.2

ΚΕΦΑΛΑΙΟ

Αλγόριθμοι

Η συνάρτηση Ο καλείται πολυωνυμική αν είναι έκφραση πολυωνύμου ως προς n, διαφορετικά καλείται μη-πολυωνυμική, αν περιέχει όρους όπως 2n, n! κτλ. Στην πράξη οι τρεις τελευταίες πολυπλοκότητες χρησιμοποιούνται μόνο για προβλήματα μικρού μεγέθους.

Για το πρόβλημα της ταξινόμησης ενός πίνακα δεν έχει βρεθεί μέχρι σήμερα ταχύτερος αλγόριθμος από τον αλγόριθμο γρήγορης ταξινόμησης, ενώ για το πρόβλημα του υπολογισμού του ΜΚΔ δεν έχει βρεθεί ταχύτερος αλγόριθμος από εκείνον του Ευκλείδη. Αυτό οδηγεί, μοιραία, στο ερώτημα: Μήπως δεν υπάρχει καλύτερος αλγόριθμος, μήπως δηλαδή τα προβλήματα αυτά έχουν μία εγγενή πολυπλοκότητα;

Σειριακοί λέγονται οι αλγόριθμοι που χρησιμοποιούν μία κεντρική μονάδα επεξεργασίας και οι εντολές τους εκτελούνται σε σειρά η μία μετά την άλλη.

Παράλληλοι χαρακτηρίζονται οι αλγόριθμοι που χρησιμοποιούν πολλαπλές κεντρικές μονάδες επεξεργασίας όπου ορισμένες ή μία σειρά από εντολές εκτελούνται παράλληλα (ταυτόχρονα).

Παράδειγμα 2.5. Έστω ότι υπάρχει ένας πίνακας που έχει ως περιεχόμενο τους αριθμούς:

1	2	3	4
6	9	8	3

Στόχος είναι να τοποθετηθούν οι αριθμοί σε αύξουσα σειρά από το μικρότερο στο μεγαλύτερο (αύξουσα ταξινόμηση). Η διαδικασία ταξινόμησης θα επιχειρηθεί με σειριακή και παράλληλη επεξεργασία.

Απάντηση

➢ Σειριακά

Εντοπίζεται το μικρότερο στοιχείο του πίνακα (στην περίπτωση αυτή είναι το 3) και αντιμετατίθεται με το στοιχείο της πρώτης θέσης.

Εντοπίζεται το μικρότερο από τα υπόλοιπα στοιχεία του πίνακα (που είναι το 6) και αντιμετατίθεται με το στοιχείο της δεύτερης θέσης.

Εντοπίζεται το μικρότερο από τα υπόλοιπα στοιχεία του πίνακα (που είναι το 8), το οποίο όμως είναι το τρίτο στοιχείο του πίνακα, οπότε η ταξινόμηση έχει ολοκληρωθεί.

➢ Παράλληλα

Συγκρίνονται ταυτόχρονα με δύο διαφορετικούς επεξεργαστές το 1ο με το 2ο στοιχείο και το 3ο με το 4ο. Αν δεν είναι σωστά διαταγμένα, αντιμετατίθενται.

Συγκρίνονται ταυτόχρονα με δύο διαφορετικούς επεξεργαστές το 1ο με το 3ο στοιχείο και το 2ο με το 4ο. Αν δεν είναι σωστά διαταγμένα, αντιμετατίθενται.

Τώρα το μικρότερο από όλα τα στοιχεία είναι στη σωστή θέση (την 1η) και το μεγαλύτερο επίσης στη σωστή θέση (την 4η). Ωστόσο τα δύο μεσαία στοιχεία δεν είναι βέβαιο ότι είναι σωστά διαταγμένα. Οπότε απαιτείται μια ακόμη σύγκριση αυτών των δύο από έναν επεξεργαστή και ολοκληρώνεται η ταξινόμηση.

Οι αλγόριθμοι επιλύουν προβλήματα. Υπάρχουν απλά και σύνθετα προβλήματα. Λίγα απλά προβλήματα μπορούν να επιλυθούν με διαδοχική εκτέλεση μερικών βημάτων, αφού τα περισσότερα προβλήματα απαιτούν την εκτέλεση ορισμένων συγκεκριμένων βημάτων πολλές φορές. Αυτοί οι αλγόριθμοι αποκαλούνται επαναληπτικοί.

Παράδειγμα 2.6. Να αναπτυχθεί αλγόριθμος ο οποίος θα διαβάζει τον αριθμό Ν και θα υπολογίζει και θα εμφανίζει το Ν παραγοντικό (συμβολισμός: Ν!).

Το Ν! ορίζεται ως το γινόμενο των ακέραιων αριθμών 1, 2 έως Ν. Δηλαδή
Ν!=1·2·3·….· (Ν-1) ·Ν

Αν Ν = 5, το 5! = 1·2·3·4·5 = 120

2η

ENOTHTA

Θέματα Θεωρητικής
Επιστήμης των Υπολογιστών

Ο πίνακας του παραδείγματος 2.5 είναι μονοδιάστατος πίνακας που έχει τέσσερα στοιχεία, στις θέσεις 1, 2, 3, 4. Στη θέση 1 το περιεχόμενο του πίνακα είναι 6, στη θέση 2 το περιεχόμενο του πίνακα είναι 9 κτλ.

Δεν μπορούν να λυθούν όλα τα προβλήματα κάνοντας χρήση παράλληλου υπολογισμού. Το σε βάθος σκάψιμο για να ανοιχτεί ένα χαντάκι δεν μπορεί να υλοποιηθεί με παράλληλο αλγόριθμο, αφού το δεύτερο μέτρο δεν είναι προσβάσιμο αν δεν τελειώσει πρώτα το πρώτο μέτρο.

Ο αλγόριθμος υπολογισμού του Ν! με μια επανάληψη βρίσκει το γινόμενο (βλέπε παράδειγμα 2.20).

Όμως το Ν! μπορεί να οριστεί και με άλλο τρόπο, που αποκαλείται αναδρομικός, ως εξής:

{

Ν! = Ν·(Ν-1)! για Ν ≥ 1
0! = 1

(1)
(2)

Από τη σχέση (1) φαίνεται ότι το παραγοντικό του Ν ορίζεται χρησιμοποιώντας το παραγοντικό του (Ν - 1). Ο όρος αναδρομικότητα εδώ εκφράζει, ότι για να βρεθεί η τιμή του Ν! πρέπει να βρεθεί η τιμή του (Ν - 1)!, η τιμή του οποίου χρειάζεται την τιμή του (Ν - 2)! κ.ο.κ.

Έτσι το 5! κάνει διαδοχικά:

5! = 4!·5 = 3!·4·5=2!·3·4·5=1!·2·3·4·5=0!·1·2·3·4·5=1·1·2·3·4·5=120

Φαίνεται ότι ο υπολογισμός του Ν! με αναδρομικό τρόπο είναι πιο πολύπλοκος από τον επαναληπτικό. Ωστόσο σε άλλες περιπτώσεις και ιδίως σε μερικά δύσκολα προβλήματα η αναδρομή διευκολύνει σημαντικά.

2.2.5 Αναπαράσταση αλγορίθμου

Προκειμένου να επιτευχθεί η «ακριβής περιγραφή» ενός αλγορίθμου, χρησιμοποιείται κάποια γλώσσα που μπορεί να περιγράφει σειρές ενεργειών με τρόπο αυστηρό, χωρίς ασάφειες και διφορούμενα. Τέτοιες γλώσσες είναι οι γλώσσες προγραμματισμού (με την προϋπόθεση ότι η σημασιολογία τους είναι αυστηρά διατυπωμένη), μαθηματικά μοντέλα, κάποιες συμβολικές γλώσσες που χρησιμοποιούν αυστηρά καθορισμένους κανόνες περιγραφής, καθώς και κατάλληλα διαμορφωμένα υποσύνολα των φυσικών (ομιλούμενων) γλωσσών.

Η αναπαράσταση των αλγορίθμων μπορεί να πραγματοποιηθεί με:

Φυσική γλώσσα όπου η αναπαράσταση γίνεται με την ομιλούμενη γλώσσα, μέσω της οποίας περιγράφονται τα βήματα επίλυσης του προβλήματος. Ωστόσο, με τη φυσική γλώσσα μπορούν να παρατηρηθούν ασάφειες στις οδηγίες.
Ψευδοκώδικα ή ψευδογλώσσα η οποία είναι μια υποθετική γλώσσα για την αναπαράσταση αλγορίθμων με στοιχεία από κάποιες γλώσσες προγραμματισμού, παραλείποντας λεπτομέρειες που δεν είναι ουσιαστικές για την ανθρώπινη κατανόηση του αλγορίθμου.
Γλώσσα προγραμματισμού η οποία είναι μια τεχνητή γλώσσα, που έχει αναπτυχθεί για να δημιουργεί ή να εκφράζει προγράμματα για τον υπολογιστή. Η αναπαράσταση των αλγορίθμων με γλώσσα προγραμματισμού μπορεί να γίνει είτε με οπτικές είτε με κειμενικές γλώσσες προγραμματισμού.

2.2

ΚΕΦΑΛΑΙΟ

Αλγόριθμοι

Ενδιαφέρον ζήτημα αποτελεί ο εντοπισμός του καλύτερου τρόπου υποδιαίρεσης των προβλημάτων, για να είναι εφικτή η επεξεργασία τους από πολλούς επεξεργαστές παράλληλα.

Για παράδειγμα, επαναληπτικοί αλγόριθμοι είναι ο ευκλείδειος αλγόριθμος, καθώς και ο αλγόριθμος ταξινόμησης με επιλογή που περιγράφηκε πιο πριν.

Αλγόριθμοι που υλοποιούν μια αναδρομική σχέση, αποκαλούνται αναδρομικοί και μερικά παραδείγματα παρουσιάζονται στην παράγραφο 2.2.7.6.

Όταν περιγράφεται στην ομιλούμενη γλώσσα ο τρόπος με τον οποίο θα μπορέσει κάποιος να επισκεφθεί ένα μουσείο, τότε ο αλγόριθμος έχει διατυπωθεί με φυσική γλώσσα.

Οι φυσικές γλώσσες, είναι οι γλώσσες που μιλούν οι άνθρωποι, ενώ οι τεχνητές γλώσσες έχουν αναπτυχθεί κυρίως για διευκόλυνση της επικοινωνίας ιδεών.

Στις οπτικές γλώσσες προγραμματισμού, η αναπαράσταση των αλγορίθμων γίνεται μέσα από το γραφικό χειρισμό προγραμματιστικών στοιχείων.
Στις κειμενικές γλώσσες προγραμματισμού, η αναπαράσταση των αλγορίθμων γίνεται με τη χρήση σειρών κειμένου που περιλαμβάνουν λέξεις, αριθούς και σημεία στίξης.

Μεθοδολογίες διαγραμματικής αναπαράστασης αλγορίθμων που συνιστούν έναν γραφικό τρόπο παρουσίασης του αλγόριθμου. Από τις διάφορες μεθοδολογίες διαγραμματικής αναπαράστασης αλγορίθμων που έχουν επινοηθεί η πιο διαδεδομένη είναι το διάγραμμα ροής, όπου η περιγραφή και η αναπαράσταση των αλγορίθμων γίνεται με τη χρήση γεωμετρικών σχημάτων - συμβόλων, όπου το καθένα δηλώνει μια συγκεκριμένη ενέργεια ή λειτουργία.

Παράδειγμα 2.7. Να αναπτυχθεί αλγόριθμος με φυσική γλώσσα, με διάγραμμα ροής και με ψευδογλώσσα, ο οποίος θα διαβάζει τις τιμές δύο μεταβλητών και θα αντιμεταθέτει το περιεχόμενό τους. Στη συνέχεια θα εμφανίζει ως αποτέλεσμα το περιεχόμενο των μεταβλητών μετά την αντιμετάθεση.

Να εκτελεστεί ο αλγόριθμος για τις τιμές 8 και 12.

Απάντηση

Φυσική γλώσσα: Αφού εισαχθούν οι τιμές δύο μεταβλητών α και β, να δώσετε το περιεχόμενο της μεταβλητής α και σε μία νέα μεταβλητή temp (προσωρινή). Στη συνέχεια, να δώσετε το περιεχόμενο της μεταβλητής β στη μεταβλητή α και τέλος να δώσετε το περιεχόμενο της μεταβλητής temp και στη μεταβλητή β.

Ψευδογλώσσα

Αλγόριθμος Αντιμετάθεση
Διάβασε α, β
temp ← α
α ← β
β ← temp
Εμφάνισε α, β
Τέλος Αντιμετάθεση

Αρ. Εντ.	α	β	temp	Έξοδος
2	8	12
3			8
4	12
5		8
6				12 8

Διάγραμμα ροής

2η

ENOTHTA

Θέματα Θεωρητικής
Επιστήμης των Υπολογιστών

Τα κυριότερα χρησιμοποιούμενα γεωμετρικά σχήματα - σύμβολα στα διαγράμματα ροής είναι τα ακόλουθα:

Η έλλειψη, που δηλώνει την αρχή και το τέλος του αλγορίθμου.
Το πλάγιο παραλληλόγραμμο, που δηλώνει είσοδο ή έξοδο στοιχείων.
Το ορθογώνιο παραλληλόγραμμο, που δηλώνει την εκτέλεση μιας ή περισσότερων πράξεων.
Ο ρόμβος, που δηλώνει μία ερώτηση με δύο εξόδους για απάντηση.
Στα διαγράμματα ροής, εκτός των παραπάνω σχημάτων, χρησιμοποιείται και το βέλος, το οποίο δείχνει τη ροή εκτέλεσης του αλγορίθμου.

Ο αλγόριθμος Αντιμετάθεση αντιμεταθέτει το περιεχόμενο των δύο μεταβλητών και παρουσιάζεται με τρεις τρόπους αναπαράστασης.

Στην ψευδογλώσσα έχουν καταγραφεί οι ενέργειες που περιγράφονται στο πλαίσιο της φυσικής γλώσσας σε κωδικοποιημένη μορφή, ενώ τέλος έχει δημιουργηθεί και το αντίστοιχο διάγραμμα ροής.

2.2.6 Δεδομένα και αναπαράστασή τους

Ένας αλγόριθμος λαμβάνει κάποια δεδομένα από την είσοδο, τα επεξεργάζεται μέσα από μια σειρά βημάτων και δίνει ως έξοδο τα αποτελέσματα.

Η επεξεργασία δεδομένων, η οποία στην πράξη πραγματοποιείται μέσω αλγορίθμων, αναφέρεται στην εκτέλεση διαφόρων πράξεων/ λειτουργιών πάνω στα δεδομένα. Το αποτέλεσμα της επεξεργασίας δεδομένων είναι η πληροφορία. Έτσι, θα μπορούσε κανείς γενικεύοντας να πει ότι ένας αλγόριθμος μετατρέπει τα δεδομένα σε πληροφορία. Για παράδειγμα, ένας τηλεφωνικός αριθμός και ένα ονοματεπώνυμο αποτελούν δεδομένα. Δεν παρέχουν όμως καμία πληροφορία. Πληροφορία παράγεται μόνο αν σχετισθούν μεταξύ τους, ότι δηλαδή κάποιο τηλέφωνο ανήκει σε κάποιο συγκεκριμένο συνδρομητή. Με βάση τις πληροφορίες λαμβάνονται αποφάσεις και γίνονται διάφορες ενέργειες. Στη συνέχεια οι ενέργειες αυτές παράγουν νέα δεδομένα, αυτά νέες πληροφορίες, οι τελευταίες νέες αποφάσεις και ενέργειες κ.ο.κ. όπως φαίνεται στην εικόνα 2.11. Η διεργασία αυτή μπορεί να επαναλαμβάνεται, οι πληροφορίες που παρήχθησαν, να επανατροφοδοτούν μέσω ανάδρασης την είσοδο για επανάληψη του κύκλου κ.ο.κ..

Η θεωρία αλγορίθμων, μελετά τα δεδομένα κυρίως από τις σκοπιές του υλικού και των γλωσσών προγραμματισμού.

Όσον αφορά τις γλώσσες προγραμματισμού, κάθε γλώσσα μπορεί να υποστηρίζει τη χρήση διαφόρων τύπων δεδομένων. Κάθε γλώσσα έχει συγκεκριμένους τύπους δεδομένων, ενώ μπορούν να δημιουργηθούν νέοι τύποι ορισμένοι από το χρήστη. Οι πιο συνήθεις τύποι δεδομένων είναι οι ακόλουθοι (εικόνα 2.12):

Ακέραιος τύπος: για την αναπαράσταση ακεραίων αριθμών.

Πραγματικός τύπος: για την αναπαράσταση πραγματικών αριθμών.

Λογικός τύπος: για την αναπαράσταση λογικών δεδομένων.

Αλφαριθμητικός τύπος: για την αναπαράσταση αλφαριθμητικών δεδομένων.

Σε κάθε τύπο δεδομένων μπορούν να εφαρμοστούν διαφορετικές πράξεις. Επομένως, κατά τον σχεδιασμό ενός αλγορίθμου έχει σημασία το είδος των τύπων δεδομένων που υποστηρίζονται.

Το υλικό επιτρέπει την αποθήκευση των δεδομένων ενός προγράμματος στην κύρια μνήμη ή και στις περιφερειακές συσκευές ενός υπολογιστή με διάφορες μορφές. Με σκοπό την πρόσβαση στα δεδομένα που βρίσκονται στη βοηθητική μνήμη είναι πιθανό να χρησιμοποιούνται διαφορετικοί αλγόριθμοι για την επεξεργασία τους. Επομένως, το υλικό του υπολογιστή έχει επίδραση στο είδος των αλγορίθμων που θα χρησιμοποιηθούν.

Τα δεδομένα μπορεί να είναι απλές μεταβλητές, οι οποίες λαμβάνουν μία τιμή κάθε φορά (απλά δεδομένα) ή μπορούν να αποθηκεύονται ως μία δομή δεδομένων.

2.2

ΚΕΦΑΛΑΙΟ

Αλγόριθμοι

Εικόνα 2.11. Σχέση δεδομένων και πληροφοριών

Εικόνα 2.12. Τύποι Δεδομένων

Ο σκληρός δίσκος και η μνήμη flash, αποτελούν παραδείγματα βοηθητικής μνήμης του υπολογιστή.

Δομή δεδομένων (data structure) είναι ένα σύνολο αποθηκευμένων δεδομένων, τα οποία είναι έτσι οργανωμένα, ώστε να υπόκεινται σε συγκεκριμένες απαιτούμενες επεξεργασίες.

Ο όρος αναφέρεται σε ένα σύνολο δεδομένων μαζί με ένα σύνολο λειτουργιών που επιτρέπονται στα δεδομένα αυτά. Οι δομές δεδομένων είναι πολύ στενά συνδεδεμένες με την έννοια του αλγορίθμου. Είναι πολύ χαρακτηριστική η ακόλουθη «σχέση» που διατύπωσε ο Νικλάους Βιρθ (Niklaus Wirth), δημιουργός της γλώσσας Pascal:

Αλγόριθμοι + Δομές Δεδομένων = Προγράμματα

Η ανωτέρω σχέση έχει την έννοια ότι αν κάποιος διαθέτει τον κατάλληλο αλγόριθμο και τις δομές δεδομένων, οι οποίες θα χρησιμοποιηθούν, είναι εντελώς άμεση η μετατροπή και υλοποίησή του σε πρόγραμμα σε γλώσσα υπολογιστή. Κάθε δομή δεδομένων αποτελείται, στην πιο γενική της μορφή, από ένα σύνολο στοιχείων ή κόμβων.

Οι πιο ευρέως χρησιμοποιούμενες δομές δεδομένων είναι ο πίνακας, η στοίβα, η ουρά, η λίστα, το δένδρο και ο γράφος.

O πίνακας (table) αποτελείται από ένα σύνολο ομοειδών απλών στοιχείων, καθένα από τα οποία καθορίζεται με τη βοήθεια ενός ή περισσοτέρων δεικτών. Ένας πίνακας μπορεί να είναι μίας, δύο ή περισσοτέρων διαστάσεων, ανάλογα με το πλήθος δεικτών που χρειάζονται για να καθοριστεί η θέση του. Στην εικόνα 2.13, παρουσιάζεται ένας δισδιάστατος πίνακας Α με 4 γραμμές και 3 στήλες. Στο παράδειγμα 2.5 είχε παρουσιαστεί ένας μονοδιάστατος πίνακας.

Μία στοίβα (stack) είναι μια γραμμική διάταξη στοιχείων, στην οποία εισάγονται και εξάγονται στοιχεία μόνο από το ένα άκρο (εικόνα 2.14). Η λειτουργία της εισαγωγής αποκαλείται ώθηση (push) και της εξαγωγής απώθηση (pull ή pop). Η φιλοσοφία εισαγωγής και εξαγωγής των στοιχείων ονομάζεται LIFO (Last In, First Out), δηλαδή το τελευταίο εισαγόμενο δεδομένο εξέρχεται και πρώτο.

Μια ουρά (queue) αποτελεί μια γραμμική διάταξη στοιχείων, στην οποία εισάγονται νέα στοιχεία από ένα άκρο και εξάγονται υπάρχοντα στοιχεία από το άλλο άκρο (εικόνα 2.15). Η λειτουργία της ουράς αποκαλείται FIFO (First In, First Out), δηλαδή το στοιχείο το οποίο εισάγεται πρώτο στην ουρά εξέρχεται και πρώτο.

Σε μια (συνδεσμική) λίστα (linked list) τα στοιχεία φαίνονται «λογικά» ότι είναι γραμμικά διατεταγμένα, χωρίς όμως αυτό να σημαίνει ότι βρίσκονται σε συνεχόμενες θέσεις της μνήμης του υπολογιστή (εικόνα 2.16). Ανεξάρτητα από τη θέση που καταλαμβάνει στη μνήμη ένα δεδομένο, συσχετίζεται με το επόμενό του με τη βοήθεια κάποιου δείκτη (pointer).

2η

ENOTHTA

Θέματα Θεωρητικής
Επιστήμης των Υπολογιστών

Δισδιάστατος Πίνακας Α 4x3
Στοιχείο 1,1	Στοιχείο 1,2	Στοιχείο 1,3
Στοιχείο 2,1	Στοιχείο 2,2	Στοιχείο 2,3
Στοιχείο 3,1	Στοιχείο 3,2	Στοιχείο 3,3
Στοιχείο 4,1	Στοιχείο 4,2	Στοιχείο 4,3

Εικόνα 2.13. Δισδιάστατος πίνακας

Εικόνα 2.14. Στοίβα

Εικόνα 2.15. Ουρά

Εικόνα 2.16. Λίστα

Τo δένδρο (tree) είναι μη γραμμική δομή που αποτελείται από ένα σύνολο κόμβων, οι οποίοι συνδέονται με ακμές (εικόνα 2.17). Υπάρχει μόνο ένας κόμβος, από τον οποίο μόνο ξεκινούν ακμές, που ονομάζεται ρίζα (root). Σε όλους τους άλλους κόμβους καταλήγει μία ακμή και ξεκινούν καμία, μία ή περισσότερες. Οι κόμβοι στους οποίους καταλήγουν μόνο ακμές, ονομάζονται φύλλα.

Ο γράφος (graph) αποτελεί τη πιο γενική δομή δεδομένων μια και αποτελείται από κόμβους και ακμές χωρίς όμως κάποια ιεράρχηση.

Υπάρχουν διάφοροι τρόποι διάκρισης των δομών δεδομένων. Διακρίνονται σε στατικές και δυναμικές. Οι στατικές δομές έχουν σταθερό μέγεθος και μπορούν να κατακρατήσουν συγκεκριμένο πλήθος στοιχείων. Αντίθετα οι δυναμικές δομές δεν έχουν σταθερό μέγεθος και το πλήθος των στοιχείων τους μπορεί να μεγαλώνει ή να μικραίνει καθώς στη δομή εισάγονται νέα δεδομένα ή διαγράφονται άλλα.

Οι δομές δεδομένων διακρίνονται επίσης σε γραμμικές και μη γραμμικές. Στις γραμμικές δομές μπορεί να ορισθεί κάποια σχέση διάταξης για δύο οποιαδήποτε διαδοχικά στοιχεία τους. Αυτό σημαίνει ότι κάποιο στοιχείο θα είναι πρώτο και κάποιο τελευταίο. Οποιοδήποτε από τα υπόλοιπα θα έπεται από το προηγούμενό του και θα προηγείται από το επόμενό του. Στις μη γραμμικές δομές δεν μπορεί να οριστεί μια σχέση διάταξης όπως η παραπάνω. Τέτοιες δομές είναι τα δένδρα και οι γράφοι. Στα δένδρα ένας κόμβος έχει έναν προηγούμενο αλλά πιθανόν πολλούς επόμενους. Στους γράφους κάθε κόμβος μπορεί να έχει πολλούς προηγούμενους και πολλούς επόμενους.

Τέλος διάκριση των δομών μπορεί να γίνει και ανάλογα με το είδος της χρησιμοποιούμενης μνήμης (κύρια ή βοηθητική). Οι δομές δεδομένων βοηθητικής μνήμης αποκαλούνται αρχεία δεδομένων (data files). Ένα αρχείο απαρτίζεται από έναν αριθμό ομοειδών εγγραφών (records). Κάθε εγγραφή διαθέτει ορισμένα πεδία (fields), που περιέχουν δεδομένα για μια οντότητα (π.χ. μαθητής), όπως φαίνεται στην εικόνα 2.19.

2.2.7 Εντολές και δομές αλγορίθμου

Στην παράγραφο αυτή δίδονται διάφορα παραδείγματα αλγορίθμων, όπου εξετάζονται τα συστατικά μέρη ενός αλγορίθμου και οι τρεις συνιστώσες του (δομή ακολουθίας, δομή επιλογής και δομή επανάληψης) ξεκινώντας από τις απλούστερες και προχωρώντας προς τις συνθετότερες. Στα περιθώρια παρουσιάζονται ορισμένα βασικά εισαγωγικά στοιχεία της χρησιμοποιούμενης ψευδογλώσσας.

Κάθε αλγόριθμος διατυπωμένος σε ψευδογλώσσα ξεκινά με τη γραμμή

Αλγόριθμος όνομα_αλγορίθμου

και τελειώνει με τη γραμμή

Τέλος όνομα_αλγορίθμου

2.2

ΚΕΦΑΛΑΙΟ

Αλγόριθμοι

Εικόνα 2.17. Δένδρο

Εικόνα 2.18. Γράφος

Για παράδειγμα, η εγγραφή ενός μαθητή μπορεί να αποτελείται από το όνομα, το επώνυμο, τον αριθμό κινητού τηλεφώνου, τη διεύθυνση αλληλογραφίας, την ηλεκτρονική διεύθυνση, τη φωτογραφία του κ.ά., που καλούνται πεδία της εγγραφής.

Εικόνα 2.19. Δομή αρχείου

Αλφάβητο

Το σύνολο των χαρακτήρων που χρησιμοποιούνται στην ψευδογλώσσα περιλαμβάνει:

όλα τα γράμματα της ελληνικής ή αγγλικής αλφαβήτου πεζά και κεφαλαία
τους αριθμητικούς χαρακτήρες 0-9
τους επόμενους ειδικούς χαρακτήρες
- '' εισαγωγικά (διπλά)
- ( ) παρενθέσεις
- [ ] αγκύλες
- * αστερίσκος
- + συν
- , κόμμα
- - μείον
- . τελεία
- / κάθετος
- ! θαυμαστικό
- < μικρότερο από
- = ίσον
- > μεγαλύτερο από
- ≤ μικρότερο ή ίσο

Μεταξύ αυτών των δύο γραμμών γράφονται οι εντολές του αλγορίθμου. Οι εντολές είναι λέξεις (συνήθως ρήματα σε προστακτική) ή συμβολισμοί που προσδιορίζουν μία σαφή ενέργεια. Οι λέξεις που έχουν αυστηρά καθορισμένο νόημα στην ψευδογλώσσα καλούνται δεσμευμένες λέξεις και στο πλαίσιο του βιβλίου θα γράφονται με έντονα μπλε γράμματα.

Οι εντολές γράφονται σε ξεχωριστές γραμμές. Επεξηγηματικά σχόλια μπορούν να γράφονται οπουδήποτε στο σώμα του αλγορίθμου. Ένα σχόλιο αρχίζει με το χαρακτήρα θαυμαστικό (!) και στο πλαίσιο του βιβλίου θα γράφεται με πλάγια γράμματα.

Στη συνέχεια επεξηγούνται οι διάφορες εντολές που μπορούν να χρησιμοποιηθούν για τη σύνταξη ενός αλγορίθμου.

2.2.7.1 Εκχώρηση, Είσοδος και Έξοδος τιμών

Η γενική μορφή της εντολής εκχώρησης είναι:

Μεταβλητή ← Έκφραση

και η λειτουργία της είναι «εκτελούνται οι πράξεις στην έκφραση και η τιμή της εκχωρείται (αποδίδεται, μεταβιβάζεται) στη μεταβλητή».

Στην εντολή χρησιμοποιείται το αριστερό βέλος προκειμένου να δείχνει τη φορά της εκχώρησης. Για το σκοπό αυτό χρησιμοποιούνται διάφορα σύμβολα από τις γλώσσες προγραμματισμού. Για παράδειγμα στην Pascal και Delphi χρησιμοποιείται το :=, ενώ στην Basic και τη C το =. Προσοχή, λοιπόν, το σύμβολο της ισότητας ( = ) στις γλώσσες προγραμματισμού ή το αριστερό βέλος ( ← ) στην ψευδογλώσσα, δεν είναι σύμβολο εξίσωσης. Το σύμβολο = χρησιμοποιείται ως τελεστής σύγκρισης.

Αριστερά του συμβόλου ← υπάρχει πάντα μόνο μια μεταβλητή, ενώ δεξιά μπορεί να υπάρχει σταθερά, μεταβλητή ή έκφραση.

Η εκχώρηση τιμών επιτυγχάνεται και με τις εντολές εισόδου. Η εντολή

Διάβασε λίστα_μεταβλητών

επιτρέπει την είσοδο τιμών και την εκχώρηση αυτών στις μεταβλητές που αναφέρονται στη λίστα_μεταβλητών.

Η εντολή Διάβασε διαφέρει από την εντολή εκχώρησης, γιατί στη δεύτερη οι τιμές των μεταβλητών προσδιορίζονται κατά τη συγγραφή του αλγορίθμου, ενώ στην πρώτη κατά την εκτέλεση του αλγορίθμου.

Για την έξοδο τιμών (αποτελεσμάτων) μπορούν να χρησιμοποιηθούν οι εντολές Γράψε, Εμφάνισε ή Εκτύπωσε με ίδια σύνταξη. Κάθε μία από αυτές τις εντολές συνοδεύεται από μια λίστα μεταβλητών ή σταθερών. Π.χ. Γράψε ''Τιμή:'', αξία.

2η

ENOTHTA

Θέματα Θεωρητικής
Επιστήμης των Υπολογιστών

≥ μεγαλύτερο ή ίσο
≠ διάφορο
^ άνω βέλος
_ κάτω παύλα
κενό

και ένα γραφικό σύμβολο το ← (αριστερό βέλος)

Σταθερές

Οι σταθερές στην ψευδογλώσσα μπορεί να είναι αριθμητικές, αλφαριθμητικές ή λογικές. Για το σχηματισμό μιας αριθμητικής σταθεράς χρησιμοποιούνται οι αριθμητικοί χαρακτήρες και πιθανά ένας από τους χαρακτήρες +, -. Επίσης, μπορεί να χρησιμοποιηθεί το κόμμα για το δεκαδικό σημείο. Π.χ. 5, 123,27, -1, 1000000 κ.λπ.
Για το σχηματισμό μιας αλφαριθμητικής σταθεράς χρησιμοποιούνται οποιοιδήποτε χαρακτήρες περικλειόμενοι σε διπλά εισαγωγικά.
Μια σταθερά μπορεί να έχει οποιοδήποτε πλήθος αριθμητικών ή αλφαριθμητικών χαρακτήρων αντίστοιχα.
Οι λογικές σταθερές είναι δύο, η Αληθής και Ψευδής.

Μεταβλητές

Για το σχηματισμό του ονόματος μιας μεταβλητής χρησιμοποιείται οποιοσδήποτε αριθμός αλφαβητικών ή αριθμητικών χαρακτήρων και ο χαρακτήρας κάτω παύλα. Ο πρώτος χαρακτήρας της μεταβλητής πρέπει να είναι αλφαβητικός και δεν μπορεί να χρησιμοποιηθεί δεσμευμένη λέξη ως όνομα μεταβλητής.
Οι μεταβλητές χαρακτηρίζονται ως αριθμητικές, αλφαριθμητικές ή λογικές ανάλογα με την τιμή που θα αποδοθεί σε αυτές. Πριν από την απόδοση κάποιας τιμής σε μια μεταβλητή (με εντολή εισόδου ή εκχώρησης) η μεταβλητή έχει απροσδιόριστη τιμή.
Οι σταθερές και οι μεταβλητές καλούνται και τελεστέοι.

2.2.7.2 Δομή ακολουθίας

Η δομή ακολουθίας χρησιμοποιείται για την αντιμετώπιση προβλημάτων στα οποία οι εντολές εκτελούνται η μία μετά την άλλη από πάνω προς τα κάτω.

Παράδειγμα 2.8. Είσοδος και έξοδος αριθμών

Να διαβαστούν δύο αριθμοί και να υπολογιστεί και να εμφανιστεί το άθροισμά τους.

Αλγόριθμος Άθροισμα

Διάβασε α, β

Σ ← α + β

Εμφάνισε Σ

Τέλος Άθροισμα

Η πρώτη ενέργεια που γίνεται είναι η εισαγωγή δεδομένων. Αυτό επιτυγχάνεται με τη χρήση της εντολής Διάβασε. Μετά την εκτέλεση της εντολής αυτής στις μεταβλητές α και β έχουν εκχωρηθεί τιμές, οπότε υπάρχει η δυνατότητα επεξεργασίας των τιμών. Εδώ απαιτείται η πρόσθεση των δύο αριθμών και η απόδοση του αθροίσματος σε μια άλλη μεταβλητή, τη Σ, που επιτυγχάνεται με την επόμενη εντολή εκχώρησης. Τελευταία ενέργεια αποτελεί η εμφάνιση (ή εκτύπωση) του αποτελέσματος.

Παράδειγμα 2.9. Υπολογισμός τελικής αξίας είδους

Να γραφεί αλγόριθμος, ο οποίος να διαβάζει την καθαρή αξία ενός είδους και το ποσοστό ΦΠΑ και να υπολογίζει και να εκτυπώνει την τελική αξία.

Αλγόριθμος Υπολογισμός

Διάβασε ΚΑ, ΠΦΠΑ

ΤΑ ← ΚΑ + ΚΑ * ΠΦΠΑ / 100

Εκτύπωσε ''Τελική Αξία:'', ΤΑ

Τέλος Υπολογισμός

Η τελική αξία (ΤΑ) ενός είδους βρίσκεται, αν στην καθαρή αξία (ΚΑ) προστεθεί η αξία ΦΠΑ. Αυτό επιτυγχάνεται με την εντολή εκχώρησης.

eikona_85 Ο ΦΠΑ (Φόρος Προστιθέμενης Αξίας) είναι ένας φόρος που επιβάλλεται σε κάθε προϊόν που πωλείται ή σε κάθε παρεχόμενη υπηρεσία. Σήμερα για τα περισσότερα είδη το ποσοστό του ΦΠΑ είναι 23%, για την εστίαση και είδη πρώτης ανάγκης είναι 13% και για τα βιβλία 6,5%. Όμως στα νησιά του Αιγαίου (εκτός της Κρήτης) εφαρμόζονται μειωμένοι συντελεστές. Τα ποσοστά του ΦΠΑ αλλάζουν με κυβερνητική απόφαση.

Οι εντολές εισόδου/εξόδου μπορούν να συνδυάζονται προκειμένου να είναι πιο κατανοητή η ενέργεια που απαιτείται από το χρήστη του προγράμματος που θα υλοποιεί έναν αλγόριθμο.

Εμφάνισε ''Δώστε τιμές για τα α και β''

Διάβασε α, β

2.2

ΚΕΦΑΛΑΙΟ

Αλγόριθμοι

Τελεστές

Τελεστές είναι τα σύμβολα και οι λέξεις που χρησιμοποιούνται στις διάφορες πράξεις. Υπάρχουν οι επόμενοι τελεστές:

➢ Αριθμητικοί

Οι αριθμητικοί τελεστές χρησιμοποιούνται για την εκτέλεση αριθμητικών πράξεων. Είναι οι:

+	για πρόσθεση
-	για αφαίρεση
*	για πολλαπλασιασμό
/	για διαίρεση
mod	για το υπόλοιπο ακέραιας διαίρεσης
div	για το πηλίκο ακέραιας διαίρεσης
^	για ύψωση σε δύναμη

➢ Σχεσιακοί

Οι σχεσιακοί τελεστές χρησιμοποιούνται για τη σύγκριση δύο τιμών. Το αποτέλεσμα μιας σύγκρισης είναι είτε Αληθής είτε Ψευδής. Οι σχεσιακοί ή συγκριτικοί τελεστές είναι οι επόμενοι:

<	μικρότερο
>	μεγαλύτερο
=	ίσο
≤	μικρότερο ή ίσο
≥	μεγαλύτερο ή ίσο
≠	διάφορο

Αντί των τριών τελευταίων τελεστών μπορεί να χρησιμοποιηθούν και οι συνδυασμοί των χαρακτήρων <=, >= και < > αντίστοιχα.

Εναλλακτική είσοδος και έξοδος τιμών παρέχεται με τη χρήση των εντολών Δεδομένα και Αποτελέσματα. Η εντολή Δεδομένα γράφεται δεύτερη (μετά την εντολή Αλγόριθμος) και περιγράφει εντός των συμβόλων // .... // τα δεδομένα του αλγορίθμου, δηλαδή τις μεταβλητές που έχουν ήδη κάποια τιμή. Αντίστοιχα η εντολή Αποτελέσματα γράφεται προτελευταία και περιέχει τις μεταβλητές εξόδου. Οι επόμενοι δύο αλγόριθμοι για τις ίδιες τιμές εισόδου έχουν την ίδια τιμή εξόδου.

Αλγόριθμος Άθροισμα_1

Διάβασε α, β

Σ ← α + β

Γράψε Σ

Τέλος Άθροισμα_1

Αλγόριθμος Άθροισμα_2

Δεδομένα // α, β //

Σ ← α + β

Αποτελέσματα // Σ //

Τέλος Άθροισμα_2

Η χρήση των εντολών Δεδομένα και Αποτελέσματα γενικά προτιμάται προκειμένου ο αλγόριθμος να απαλλαγεί από τις λεπτομέρειες εισόδου/εξόδου και να επικεντρωθεί στο πρόβλημα που επιλύει (εκτός βέβαια αν το πρόβλημα είναι η εισαγωγή δεδομένων). Επίσης η χρήση τους συνιστάται στην περίπτωση που τα δεδομένα εισόδου ή/και εξόδου είναι πολυπληθή, όπως για παράδειγμα σε προβλήματα επεξεργασίας πινάκων. Τέλος η χρήση τους επιβάλλεται, στην περίπτωση που ένας αλγόριθμος καλείται από άλλον (βλ. παρ. 2.2.7.5).

eikona_86 Αν και η χρήση της μιας ή της άλλης μεθόδου αφήνεται γενικά στην ευχέρεια του συντάκτη του αλγορίθμου, ο μαθητής χρειάζεται να είναι προσεκτικός στη χρήση των δύο εντολών. Έτσι αν η εκφώνηση ενός θέματος λέει «Να γραφεί αλγόριθμος ο οποίος να διαβάζει ....»», τότε είναι απαραίτητο να χρησιμοποιηθεί η εντολή Διάβασε. Αντίθετα αν η εκφώνηση λέει «Δίδεται ένας πίνακας Α. Να γραφεί αλγόριθμος ο οποίος ...», τότε χρειάζεται να χρησιμοποιηθεί η εντολή Δεδομένα.

2.2.7.3 Δομή επιλογής

Στην πράξη πολύ λίγα προβλήματα μπορούν να επιλυθούν με τον προηγούμενο τρόπο της σειριακής/ακολουθιακής δομής ενεργειών. Συνήθως τα προβλήματα έχουν κάποιες ιδιαιτερότητες και δεν μπορούν να εκτελεστούν τα ίδια βήματα για κάθε περίπτωση. Τις πιο πολλές φορές λαμβάνονται κάποιες αποφάσεις με βάση κάποια κριτήρια που μπορεί να είναι διαφορετικά για κάθε στιγμιότυπο ενός προβλήματος. Για παράδειγμα το πρόβλημα της εξόδου (από το σπίτι) σχετίζεται με τις καιρικές συνθήκες. Έτσι κάποιος μπορεί να πει ότι, «αν βρέχει, θα πάρω ομπρέλα».

Με τη δομή επιλογής μπορεί να τροποποιηθεί η σειρά εκτέλεσης των εντολών ενός αλγορίθμου. Η διαδικασία επιλογής περιλαμβάνει τον έλεγχο μιας συνθήκης που μπορεί να έχει δύο τιμές (Αληθής ή Ψευδής) και ακολουθεί η απόφαση εκτέλεσης εντολών με βάση την τιμή αυτής της συνθήκης. Ως συνθήκη εννοείται μια λογική έκφραση στην οποία υπάρχει τουλάχιστον ένας σχεσιακός τελεστής (δηλαδή η συνθήκη δεν μπορεί να απαρτίζεται από μόνο μια μεταβλητή ή μια σταθερά ή μια αριθμητική παράσταση).

2η

ENOTHTA

Θέματα Θεωρητικής
Επιστήμης των Υπολογιστών

➢ Λογικοί

Οι λογικοί τελεστές υλοποιούν τις λογικές πράξεις. Το αποτέλεσμα μιας λογικής πράξης είναι Αληθής ή Ψευδής. Λογικοί τελεστές είναι:

όχι	πράξη άρνησης
και	πράξη σύζευξης
ή	πράξη διάζευξης

➢ Συναρτησιακοί τελεστές ή Συναρτήσεις

Μια συνάρτηση χρησιμοποιείται για να εκτελέσει μια προκαθορισμένη λειτουργία. Κάθε συνάρτηση έχει ένα όνομα ακολουθούμενο από ζεύγος παρενθέσεων που περικλείουν μια μεταβλητή ή μια σταθερά ή γενικότερα μια έκφραση. Στην ψευδογλώσσα μπορούν να χρησιμοποιηθούν όλες οι συνηθισμένες συναρτήσεις, όπως οι τριγωνομετρικές ΗΜ(x), ΣΥΝ(x), ΕΦ(x), οι μαθηματικές Α_Τ(x) για την απόλυτη τιμή, Ε(x) για την ex, ΛΟΓ(x) για το δεκαδικό λογάριθμο, ΛΝ(x) για το φυσικό λογάριθμο, Τ_Ρ(x) για την τετραγωνική ρίζα, και Α_Μ(x) για το ακέραιο μέρος.

2.2

ΚΕΦΑΛΑΙΟ

Εκφράσεις

Μια έκφραση μπορεί να είναι μια σταθερά, μια μεταβλητή, μια συνάρτηση ή ένας συνδυασμός σταθερών, μεταβλητών, συναρτήσεων, τελεστών και παρενθέσεων.

Σε μία έκφραση που αποτελείται από συνδυασμό στοιχείων, εκτελούνται οι πράξεις επί των σταθερών και μεταβλητών που ορίζουν οι τελεστές. Οι χρησιμοποιούμενοι τελεστές έχουν διαφορετική ιεραρχία. Αυτό σημαίνει ότι κάποιες πράξεις μπορεί να προηγούνται από κάποιες άλλες σε μια έκφραση.

Η ιεραρχία των πράξεων είναι η ακόλουθη:

Α. Αριθμητικοί τελεστές
Σε κάθε έκφραση που υπάρχουν αριθμητικοί τελεστές, ακολουθείται η προσδιορισμένη από τα μαθηματικά ιεραρχία των πράξεων.
1. Ύψωση σε δύναμη
2. Πολλαπλασιασμός, Διαίρεση, Πηλίκο ακέραιας διαίρεσης, Υπόλοιπο ακέραιας διαίρεσης
3. Πρόσθεση, Αφαίρεση

Β. Σχεσιακοί τελεστές
Γ. Λογικοί τελεστές
1. όχι
2. και
3. ή

Αν οι πράξεις είναι ίδιας ιεραρχίας, τότε εκτελούνται από τα αριστερά προς τα δεξιά.

Οι τελεστέοι ενός αριθμητικού τελεστή πρέπει να είναι αριθμητικές εκφράσεις. (π.χ. α + β^3)

Στις λογικές εκφράσεις μπορούν να χρησιμοποιηθούν όλοι οι τελεστές. Αν μία λογική έκφραση περιλαμβάνει τελεστές, τότε ένας τουλάχιστον πρέπει να είναι λογικός ή συγκριτικός. (π.χ. α + β^3 > 5 και γ / 3 < 2)

Οι συγκριτικοί τελεστές συνδυάζονται με εκφράσεις ιδίου τύπου, ενώ οι λογικοί τελεστές μόνο με λογικές εκφράσεις. (π.χ. α + β > 3, ''ΑΒ'' < ''Γ'')

Οι συγκρίσεις λογικών εκφράσεων έχουν νόημα μόνο στην περίπτωση του = και ≠.

Αριθμητικές εκφράσεις

Στη συνέχεια παρουσιάζονται μερικά παραδείγματα και διευκρινίσεις που αφορούν τις αριθμητικές εκφράσεις.

Στην έκφραση 5 + 12 / 3 * 2 - 1 οι πράξεις εκτελούνται με την επόμενη σειρά
1. 1. 12 / 3 (= 4)
2. 2. 4 * 2 (= 8)
3. 3. 5 + 8 (= 13)
4. 4. 13 - 1 (= 12)

Σε μια έκφραση μπορούν να χρησιμοποιηθούν και παρενθέσεις. Οι παρενθέσεις μπορεί να μεταβάλλουν την προτεραιότητα των πράξεων.

Στην έκφραση 4 * (1 + 2) εκτελείται πρώτα η πρόσθεση (1 + 2 = 3) και μετά ο πολλαπλασιασμός (4 * 3 = 12)
Παρατίθεται ένας πίνακας με τη γραφή μερικών μαθηματικών τύπων ως εκφράσεις της ψευδογλώσσας.

**Πίνακας 2.4.** Μαθηματικοί τύποι ως
εκφράσεις της ψευδογλώσσας
Μαθηματικός τύπος	Έκφραση ψευδογλώσσας
x - y / z	(x - y) / z
xy / z + 1	x * y /( z + 1)
(x2)3	(x^2)^3
x2³	x^(2^3)
x(-y)	x * (-y)

Στην ακέραια διαίρεση οι τελεστέοι των τελεστών div και mod είναι υποχρεωτικά θετικοί ακέραιοι αριθμοί.

Λογικές εκφράσεις

Οι σχεσιακοί τελεστές χρησιμοποιούνται για τη σύγκριση δύο τιμών. Το αποτέλεσμα μιας σύγκρισης μπορεί να είναι είτε Αληθής είτε Ψευδής.
- Στην έκφραση x + y < (z - 1) / t το αποτέλεσμα είναι Αληθής, αν το αποτέλεσμα της πράξης x + y είναι μικρότερο από το αποτέλεσμα της πράξης z - 1 διαιρούμενο δια t.
Οι σχεσιακοί τελεστές μπορούν να χρησιμοποιηθούν και με αλφαριθμητικούς τελεστέους. Η σύγκριση αλφαριθμητικών εκφράσεων πραγματοποιείται βάσει διεθνών προτύπων που στοχεύουν στην κωδικοποίηση όλων των συστημάτων γραφής. Ο υπολογισμός του αποτελέσματος, λοιπόν, της σύγκρισης αλφαριθμητικών εκφράσεων που περιέχουν οποιονδήποτε χαρακτήρα είναι πέρα από τους στόχους του μαθήματος. Για το λόγο αυτό, στην ψευδογλώσσα θα γίνεται σύγκριση αλφαριθμητικών εκφράσεων που περιέχουν μόνο τα κεφαλαία γράμματα του ελληνικού αλφαβήτου, στα οποία ισχύει η αλφαβητική σειρά. Για παράδειγμα η λογική έκφραση ''ΑΔΓ'' > ''ΑΒΚ'' είναι αληθής, διότι κατά τη σύγκριση χαρακτήρα προς χαρακτήρα από αριστερά προς τα δεξιά εντοπίζεται ότι το γράμμα Δ είναι διαφορετικό και μεγαλύτερο του γράμματος Β.

2η

ΕΝΟΤΗΤΑ

Οι λογικοί τελεστές πραγματοποιούν τις λογικές πράξεις σε μια έκφραση. Το αποτέλεσμα μιας λογικής πράξης είναι πάντα Αληθής ή Ψευδής, σύμφωνα με τον επόμενο πίνακα τιμών, όπου με Χ και Υ εννοούνται δύο λογικές εκφράσεις, στις οποίες χρησιμοποιούνται μόνο αριθμητικοί και σχεσιακοί τελεστές.

**Πίνακας 2.5.** Πίνακας τιμών δύο λογικών εκφράσεων (όχι, και, ή)
Χ	Υ	όχι Χ	Χ και Υ	Χ ή Υ
Αληθής	Αληθής	Ψευδής	Αληθής	Αληθής
Αληθής	Ψευδής	Ψευδής	Ψευδής	Αληθής
Ψευδής	Αληθής	Αληθής	Ψευδής	Αληθής
Ψευδής	Ψευδής	Αληθής	Ψευδής	Ψευδής

Σε μια λογική έκφραση οι λογικές πράξεις εκτελούνται μετά τις αριθμητικές και συγκριτικές.

Η σχέση 0 < x < 2k + 1 γράφεται στην ψευδογλώσσα x > 0 και x < 2 * k + 1 και είναι αληθής, αν x θετικό και ταυτόχρονα μικρότερο του 2 * k + 1.

Ο τελεστής όχι έχει έναν τελεστέο, ενώ οι και, ή έχουν δύο (ή περισσότερους).

Προσοχή. Ο συγκριτικός τελεστής ≤ είναι ένας και διαβάζεται «μικρότερο ή ίσο». Δεν πρέπει να αναλύεται και σε μια λογική έκφραση με χρήση του λογικού τελεστή ή, διότι υπάρχει μεγάλη πιθανότητα να προκληθεί λάθος, ιδιαίτερα αν υπάρχουν πολλοί τελεστές σε μια σύνθετη έκφραση.
Η σχέση 0 < x ≤ 10 γράφεται στην ψευδογλώσσα x > 0 και x ≤ 10

Στην πιο πάνω έκφραση δεν μπορούμε να αναλύσουμε την x ≤ 10 σε x = 10 ή x < 10, διότι θα λάβουμε την x > 0 και x = 10 ή x < 10 η οποία για x = -1 θα δώσει τιμή Αληθής.

Συνιστάται ανεπιφύλακτα να χρησιμοποιούνται παρενθέσεις όταν σε έκφραση υπάρχουν πολλοί λογικοί τελεστές.

Παράδειγμα 2.10. Να διαβαστεί ένας αριθμός και να εμφανιστεί η απόλυτη τιμή του.

Η απόλυτη τιμή ενός αριθμού είναι ο ίδιος ο αριθμός, αν είναι θετικός ή ο αντίθετός του, αν είναι αρνητικός. Έτσι για να υπολογιστεί η απόλυτη τιμή ενός αριθμού αρκεί να ελεγχθεί, αν τυχόν ο δεδομένος αριθμός είναι αρνητικός και αν ναι, να βρεθεί ο αντίθετός του. Ο συλλογισμός αυτός οδηγεί στον επόμενο αλγόριθμο.

Αλγόριθμος Απόλυτη_τιμή1

Διάβασε α

Αν α < 0 τότε

α ← α * (-1)

! α ← - α

Τέλος_αν

Εμφάνισε α

Τέλος Απόλυτη_τιμή1

Αλγόριθμος Απόλυτη_τιμή2

Διάβασε α

! Η εμφάνιση της απόλυτης τιμής

! μπορεί να γίνει με τη χρήση της

! συνάρτησης Α_Τ(α)

Εμφάνισε Α_Τ(α)

Τέλος Απόλυτη_τιμή2

Παράδειγμα 2.11. Να αναπτύξετε αλγόριθμο ο οποίος με δεδομένα τα μήκη τριών ευθυγράμμων τμημάτων θα υπολογίζει και θα εμφανίζει το εμβαδόν του τριγώνου που μπορούν να σχηματίσουν, με βάση τον τύπο του Ήρωνα Ε=√ τ (τ - α) (τ - β) (τ - γ) , όπου τ είναι η ημιπερίμετρος του τριγώνου τ = (α + β + γ) / 2 και α, β, γ τα μήκη των ευθυγράμμων τμημάτων. Σε περίπτωση που τα ευθύγραμμα τμήματα δεν

Σύγκριση αριθμών με απλή επιλογή

Απλή εντολή επιλογής

Αν Συνθήκη τότε

Εντολές

Τέλος_αν

Αν η συνθήκη είναι αληθής, τότε εκτελούνται οι εντολές.Οι εντολές μπορούν να είναι μία ή περισσότερες.

Εικόνα 2.20. Διάγραμμα ροής της απλής εντολής επιλογής

μπορούν να σχηματίσουν τρίγωνο, εμφανίζεται κατάλληλο μήνυμα. Για να σχηματιστεί τρίγωνο θα πρέπει το άθροισμα των μηκών δύο οποιονδήποτε ευθυγράμμων τμημάτων να είναι μεγαλύτερο από το μήκος του άλλου τμήματος.

Αλγόριθμος Εμβαδό

Δεδομένα // α, β, γ //

Αν α + β > γ και β + γ > α και γ + α > β τότε

τ ← (α + β + γ) / 2

Εμβ ← Τ_Ρ(τ * (τ - α) * (τ - β) * (τ - γ))

Εμφάνισε Εμβ

αλλιώς

Εμφάνισε ''Δεν σχηματίζεται τρίγωνο''

Τέλος_αν

Τέλος Εμβαδό

Παράδειγμα 2.12. Το όζον (Ο3) αποτελεί έναν από τους ρύπους που προκαλούν μόλυνση στην ατμόσφαιρα. Σε περιπτώσεις που ο ρύπος αυτός ξεπεράσει τα 300 μg/m3 τότε πρέπει να ληφθούν μέτρα. Να αναπτυχθεί αλγόριθμος ο οποίος θα διαβάζει την τιμή του Ο3 και θα εκτυπώνει το αντίστοιχο μήνυμα σύμφωνα με τον παρακάτω πίνακα:

Τιμές Ο3 (μg/m3)	Μήνυμα
Τιμή > 250	Προειδοποίηση
Τιμή > 300	Μέτρα Α
Τιμή > 500	Μέτρα Β

Επιπλέον, σε περίπτωση που έχουν ξεπεραστεί τα όρια, θα εκτυπώνει κατά πόσο τα ξεπέρασε.

Αλγόριθμος Όζον1

Διάβασε τ

Αν τ > 250 και τ ≤ 300 τότε

Εκτύπωσε ''Προειδοποίηση''

αλλιώς_αν τ > 300 και τ ≤ 500 τότε

πο ← τ - 300

Εκτύπωσε ''Μέτρα Α'', πο

αλλιώς_αν τ > 500 τότε

πο ← τ - 300

Εκτύπωσε ''Μέτρα Β'', πο

Τέλος_αν

Τέλος Όζον1

Αλγόριθμος Όζον2

Διάβασε τ

Αν τ > 500 τότε

πο ← τ - 300

Εκτύπωσε ''Μέτρα Β'', πο

αλλιώς_αν τ > 300 τότε

πο ← τ - 300

Εκτύπωσε ''Μέτρα A'', πο

αλλιώς_αν τ > 250 τότε

Εκτύπωσε ''Προειδοποίηση''

Τέλος_αν

Τέλος Όζον2

Εμφωλευμένες εντολές επιλογής

Σε όλες τις προηγούμενες περιπτώσεις όπου αναφέρεται εντολή ή εντολές, τίποτα δεν απαγορεύει αυτές οι εντολές να είναι επίσης εντολές επιλογής. Αναφερόμαστε τότε σε εμφωλευμένες εντολές επιλογής.

2.2

ΚΕΦΑΛΑΙΟ

Αλγόριθμοι

Σύνθετη εντολή επιλογής

Αν Συνθήκη τότε

Εντολές_1

αλλιώς

Εντολές_2

Τέλος_αν

Αν η συνθήκη είναι αληθής, τότε εκτελούνται οι εντολές 1, αλλιώς (δηλαδή αν η συνθήκη είναι ψευδής) εκτελούνται οι εντολές 2.

Εικόνα 2.21. Διάγραμμα ροής της σύνθετης εντολής επιλογής

Παράδειγμα 2.13. Αριθμομηχανή

Να αναπτυχθεί αλγόριθμος, ο οποίος:

1. Θα διαβάζει πρώτα έναν αριθμό α, στη συνέχεια έναν από τους χαρακτήρες +, -, *, /, ανάλογα με την πράξη που θα εκτελέσει και τέλος έναν αριθμό β.

2. Θα εκτελεί την αντίστοιχη πράξη και θα τυπώνει το αποτέλεσμα. Σε περίπτωση που έχει επιλεγεί η πράξη της διαίρεσης, ο αλγόριθμος πρέπει να ελέγχει αν το β είναι μηδέν και τότε να τυπώνει το μήνυμα «Προσοχή, διαίρεση με το μηδέν» και να οδηγείται στο τέλος του.

3. Θα εκτυπώνει το μήνυμα «Λάθος πράξη», αν για το χαρακτήρα της πράξης δοθεί άλλο σύμβολο.

Αλγόριθμος Αριθμομηχανή

Διάβασε α, πράξη, β

Αν πράξη = ''+'' τότε

Εμφάνισε α + β

αλλιώς_αν πράξη = ''-'' τότε

Εμφάνισε α - β

αλλιώς_αν πράξη = ''*'' τότε

Εμφάνισε α * β

αλλιώς_αν πράξη = ''/'' τότε

Αν β ≠ 0 τότε

Εμφάνισε α / β

αλλιώς

Εμφάνισε ''Προσοχή, διαίρεση με το μηδέν''

Τέλος_αν

αλλιώς

Εμφάνισε ''Λάθος πράξη''

Τέλος_αν

Τέλος Αριθμομηχανή

2.2.7.4 Δομή επανάληψης

Λίγοι αλγόριθμοι χρησιμοποιούν μόνο τις δομές ακολουθίας και επιλογής. Στα ρεαλιστικά προβλήματα χρειάζεται συνήθως μια σειρά εντολών να επαναληφθεί πολλές φορές. Άλλωστε σε τέτοια προβλήματα «αξίζει τον κόπο» να εκπονηθεί κάποιος αλγόριθμος και στη συνέχεια να υλοποιηθεί ένα αντίστοιχο πρόγραμμα υπολογιστή.

Οι επαναληπτικές διαδικασίες μπορεί να έχουν διάφορες μορφές και να εμπεριέχουν συνθήκες επιλογών, όπως αυτές που περιγράφηκαν στις προηγούμενες παραγράφους.

Παράδειγμα 2.14. Να εκπονηθεί αλγόριθμος ο οποίος με δεδομένο ένα θετικό ακέραιο αριθμό θα εμφανίζει τους ακέραιους αριθμούς από το 1 μέχρι και τον δεδομένο αριθμό Ν.

2η

ENOTHTA

Θέματα Θεωρητικής
Επιστήμης των Υπολογιστών

Πολλαπλή

Αν συνθήκη_1 τότε

εντολές_1

αλλιώς_αν συνθήκη_2 τότε

εντολές_2

..................

αλλιώς_αν συνθήκη_ν τότε

εντολές_ν

αλλιώς

εντολές_αλλιώς

Τέλος_αν

Αν η συνθήκη_k είναι αληθής, εκτελούνται οι εντολές_k και η συνέχεια είναι η επόμενη εντολή από το Τέλος_αν. Εφόσον καμία συνθήκη δεν είναι αληθής, τότε εκτελούνται οι εντολές_αλλιώς. Οι εντολές_αλλιώς χρησιμοποιούνται κατά περίσταση.

Σημειώνεται ότι, αν σε μια πολλαπλή εντολή επιλογής υπάρχουν πάνω από μία συνθήκες αληθείς, τότε εκτελούνται οι εντολές που ανήκουν στην πρώτη αληθή συνθήκη κατά σειρά.

Οι ζητούμενοι αριθμοί μπορούν να παραχθούν με ένα συστηματικό τρόπο, αφού ο καθένας δημιουργείται από τον προηγούμενό του προσθέτοντας το 1. Με την αξιοποίηση αυτού του γεγονότος, ο αλγόριθμος δημιουργεί κάθε νέο αριθμό σε μια μεταβλητή, έστω i. Αυτό μπορεί να γίνει με τη χρήση της εντολής εκχώρησης: i ← i + 1.

Οπότε προκύπτει το ακόλουθο:

i ← 1

Εμφάνισε i ! Εμφανίζεται το 1

i ← i + 1

Εμφάνισε i ! Εμφανίζεται το 2

i ← i + 1

Εμφάνισε i ! Εμφανίζεται το 3

…..

Το ζεύγος των εντολών i ← i + 1 και Εμφάνισε i επαναλαμβάνεται αυτούσιο. Αν μπορούσαν οι εντολές αυτές να γραφούν μία φορά και να εκτελεστούν Ν φορές, τότε το πρόβλημα θα λυνόταν. Αυτό επιτυγχάνεται με τις εντολές επανάληψης. Το πόσες φορές μπορούν να εκτελεστούν οι εντολές επανάληψης καθορίζεται με διαφορετικούς τρόπους. Στο παράδειγμα οι εντολές εκτελούνται όσο διάστημα η μεταβλητή i είναι μικρότερη ή ίση της μεταβλητής Ν.

Κατόπιν αυτών ο αλγόριθμος γίνεται

Αλγόριθμος Σειρά_αριθμών

Δεδομένα // Ν //

i ← 1

Όσο i ≤ Ν επανάλαβε

Εμφάνισε i

i ← i + 1

Τέλος_επανάληψης

Τέλος Σειρά_αριθμών

Συχνά η μεταβλητή i αποκαλείται μετρητής, επειδή αυξάνεται κατά 1. Σε άλλες περιπτώσεις όμως το βήμα αύξησης μπορεί να είναι οποιοδήποτε.

Παράδειγμα 2.15. Να γραφεί αλγόριθμος ο οποίος διαβάζει το όνομα ενός μαθητή, τους βαθμούς του σε τρία μαθήματα και υπολογίζει και τυπώνει το μέσο όρο του. Ο αλγόριθμος να σταματάει, όταν για όνομα μαθητή δοθεί το κενό εμφανίζοντας το πλήθος των μαθητών για τους οποίους υπολογίστηκε ο μέσος όρος.

Αλγόριθμος Μέσος_όρος

π ← 0

Διάβασε όνομα

Όσο όνομα ≠ '' '' επανάλαβε

2.2

ΚΕΦΑΛΑΙΟ

Αλγόριθμοι

Εντολή
Όσο ... επανάλαβε

Όσο Συνθήκη επανάλαβε

Εντολές

Τέλος_επανάληψης

Εκτελούνται οι εντολές όσο η συνθήκη είναι αληθής

Εικόνα 2.22. Διάγραμμα ροής της Όσο...επανάλαβε

Η εντολή i ← i + 1 δεν είναι εξίσωση (γιατί και να ήταν δεν έχει λύση), αλλά δρα ως εξής: κάθε φορά που εκτελείται, το περιεχόμενο της μεταβλητής i αυξάνεται κατά 1.

Όλες οι εντολές επανάληψης μπορούν να πραγματοποιούν την εκτέλεση ενός συνόλου εντολών πάνω από μια φορά.

Στην εντολή Όσο… επανάλαβε οι εμπεριεχόμενες εντολές μπορεί να μην εκτελεστούν ποτέ, αφού η συνθήκη τερματισμού ελέγχεται στην αρχή.

Οι εντολές που συγκροτούν μια εντολή επανάληψης αποκαλούνται βρόχος (αγγλ. loop, γαλ. boucle).

Προσοχή: βρόχος, όχι βρόγχος. Βρόχος = θηλιά, βρόγχος = πνευμόνι.

Διάβασε α, β, γ

Εμφάνισε (α + β + γ) / 3

π ← π + 1

Διάβασε όνομα

Τέλος_επανάληψης

Εμφάνισε π

Τέλος Μέσος_όρος

Παράδειγμα 2.16. Σε ένα σουπερμάρκετ κάθε πελάτης δικαιούται μια δωροεπιταγή 6 € αν συμπληρώσει 200 πόντους. Να αναπτυχθεί αλγόριθμος ο οποίος θα διαβάζει τους πόντους που κερδίζει ένας συγκεκριμένος πελάτης σε κάθε επίσκεψη στο σουπερμάρκετ και θα εμφανίζει μετά από πόσες επισκέψεις παίρνει τη δωροεπιταγή και ποιος είναι ο μέσος όρος πόντων σε κάθε επίσκεψη.

Αλγόριθμος Παράδειγμα

Σ ← 0

π ← 0

Όσο Σ < 200 επανάλαβε

Διάβασε πόντοι

Σ ← Σ + πόντοι

π ← π + 1

Τέλος_επανάληψης

ΜΟ ← Σ / π

Εμφάνισε π, ΜΟ

Τέλος Παράδειγμα

Παράδειγμα 2.17. Κατάλογος επιλογών

Πολύ συχνά στις εφαρμογές προβάλλεται στην οθόνη ένας κατάλογος από δυνατές επιλογές (menu) και στη συνέχεια ζητείται από το χρήστη να διαλέξει μία μόνο από αυτές. Στην πιο απλή περίπτωση, οι δυνατές επιλογές είναι αριθμημένες, οπότε απλά ζητείται η εισαγωγή ενός ακέραιου αριθμού.

…

Επανάλαβε

Εμφάνισε ''1. Ενημέρωση''

Εμφάνισε ''2. Εκτύπωση''

Εμφάνισε ''3. Έξοδος''

Εμφάνισε ''Επιλογή:''

Διάβασε Επιλογή

Μέχρις_ότου Επιλογή = 1 ή Επιλογή = 2 ή Επιλογή = 3

Στο παραπάνω τμήμα αλγορίθμου, ο βρόχος επαναλαμβάνεται μέχρι να δοθεί 1, 2 ή 3. Με τον τρόπο αυτό προστατεύεται το πρόγραμμα εφαρμογής από τυχόν λανθασμένη εισαγωγή τιμών από τον χρήστη. Ας σημειωθεί με την ευκαιρία, ότι τα προγράμματα εισαγωγής δεδομένων

2η

ENOTHTA

Θέματα Θεωρητικής
Επιστήμης των Υπολογιστών

Εντολή
Επανάλαβε ... Μέχρις_ότου

Επανάλαβε

Εντολές

Μέχρις_ότου Συνθήκη

Εκτελούνται οι εντολές μέχρις ότου η συνθήκη γίνει αληθής.

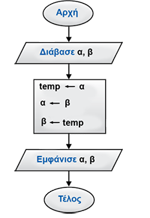
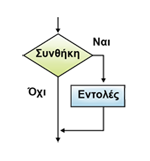
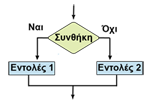
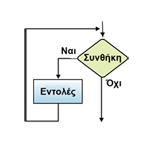
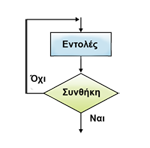Εικόνα 2.23. Διάγραμμα ροής της Επανάλαβε...Μέχρις_ότου

είναι συνήθως τα πιο δύσκολα και μακροσκελή λόγω της ανάγκης να είναι φιλικά προς το χρήστη.Υποτίθεται ότι ανάλογα με την επιλογή, ο πιο πάνω αλγόριθμος διακλαδίζεται σε άλλα σημεία, όπου υπάρχουν οι εντολές υλοποίησης κάθε λειτουργίας.

Παράδειγμα 2.18. Να εκπονηθεί αλγόριθμος ο οποίος θα διαβάζει 100 αριθμούς και θα υπολογίζει και θα εμφανίζει το άθροισμά τους.

Αλγόριθμος Άθροισμα_Αριθμών

Σ ← 0

Για i από 1 μέχρι 100

Διάβασε α

Σ ← Σ + α

Τέλος_επανάληψης

Εμφάνισε ''Άθροισμα:'', Σ

Τέλος Άθροισμα_Αριθμών

Σε αυτό το παράδειγμα η εντολή Για…από…μέχρι περιλαμβάνει όλα τα απαραίτητα δεδομένα για την επανάληψη, δηλαδή αρχική τιμή της μεταβλητής i, τελική τιμή και το βήμα μεταβολής που είναι 1 και παραλείπεται. Ο βρόχος εκτελείται για όλες τις τιμές της μεταβλητής i.

Η εντολή εκχώρησης Σ ← Σ + α δεν είναι εξίσωση και καλύτερα να διαβάζεται ως «η νέα τιμή της μεταβλητής Σ είναι η παλιά συν α».

Συχνά η μεταβλητή Σ αποκαλείται αθροιστής, γιατί της εκχωρείται το τρέχον και τελικό άθροισμα των αριθμών και δεν πρέπει να λησμονείται ότι απαιτείται ο μηδενισμός του πριν από την έναρξη της επαναληπτικής διαδικασίας.

Η χρήση της εντολής Για…από…μέχρι γενικά προτιμάται όταν είναι γνωστός ο αριθμός των φορών που θα γίνει μια επανάληψη, με άλλα λόγια όταν είναι γνωστά τα τ1, τ2 και β.

Εμφωλευμένες εντολές επανάληψης

Σε όλες τις προηγούμενες περιπτώσεις όπου αναφέρεται εντολή ή εντολές, τίποτα δεν απαγορεύει αυτές οι εντολές να είναι επίσης εντολές επανάληψης. Αναφερόμαστε τότε σε εμφωλευμένες εντολές επανάληψης.

2.2.7.5 Κλήση αλγόριθμου από αλγόριθμο

Ένας αλγόριθμος μπορεί να κληθεί από έναν άλλο αλγόριθμο με χρήση της εντολής Κάλεσε.

Η επικοινωνία μεταξύ των δύο αλγορίθμων γίνεται ως εξής:

2.2

ΚΕΦΑΛΑΙΟ

Αλγόριθμοι

Εντολή Για ... από ... μέχρι

Για μεταβλητή από τ1 μέχρι τ2 [με_βήμα β]

Εντολές

Τέλος_επανάληψης

Εκτελούνται οι εντολές με αρχική τιμή της μεταβλητής τ1 μέχρι και την τελική τιμή της μεταβλητής τ2.

Στη δομή αυτή τ1, τ2 είναι αριθμητικές σταθερές, μεταβλητές ή εκφράσεις. Πρέπει τ1 ≤ τ2, αν β > 0 και τ1 ≥ τ2, αν β < 0. Το βήμα β, αν είναι 1, παραλείπεται. Οι τιμές των τ1, τ2 και β μπορεί να είναι ακέραιες ή πραγματικές.

Αν τ1 > τ2 και β = 0 δεν θα εκτελεστούν οι εμπεριεχόμενες εντολές της Για, ενώ αν τ1 ≤ τ2 και β = 0 η εντολή επανάληψης θα εκτελείται άπειρες φορές (ατέρμονας βρόχος).

Γενικά οι εμφωλευμένες εντολές επιτρέπουν το συνδυασμό συνιστωσών ενός αλγορίθμου με οποιαδήποτε σειρά. Για παράδειγμα: Επανάληψη μέσα σε επιλογή, επανάληψη μέσα σε επανάληψη κ.α.

Παράδειγμα 2.19.

Η αντιστοιχία των μεταβλητών των δύο αλγορίθμων γίνεται με τη σειρά που αναφέρονται στις αντίστοιχες γραμμές, δηλ. α ⇒ x, β ⇒ y και γ ⇐ z1, δ ⇐ z2. Συνώνυμες μεταβλητές διαφορετικών αλγορίθμων δεν έχουν καμία σχέση μεταξύ τους.

Παράδειγμα 2.20. Υπολογισμός συνδυασμών

Να εκπονηθεί αλγόριθμος ο οποίος να υπολογίζει το πλήθος των συνδυασμών των Ν πραγμάτων ανά Κ. Ο συνδυασμός των Ν πραγμάτων ανά Κ συμβολίζεται με

(

n / k

)

και δίνεται από τον τύπο

n! / k!(n - k)!

Αλγόριθμος Παραγοντικό

Δεδομένα // n //

nfact ← 1

Για i από 2 μέχρι n

nfact ← nfact * i

Τέλος_επανάληψης

Αποτελέσματα // nfact //

Τέλος Παραγοντικό

Αλγόριθμος Συνδυασμοί

Δεδομένα //n, k//

Κάλεσε Παραγοντικό(n, nfact)

Κάλεσε Παραγοντικό(k, kfact)

Κάλεσε Παραγοντικό(n - k, nkfact)

combin ← nfact / (kfact * nkfact)

Αποτελέσματα //combin//

Τέλος Συνδυασμοί

Από τον τύπο των συνδυασμών φαίνεται ότι απαιτείται ο υπολογισμός του παραγοντικού τριών διαφορετικών ποσοτήτων. Για το σκοπό αυτό δημιουργείται ο αλγόριθμος Παραγοντικό, που υπολογίζει το παραγοντικό ενός αριθμού. Σε αυτόν τον αλγόριθμο με μια απλή επανάληψη βρίσκεται το παραγοντικό της μεταβλητής n στη μεταβλητή nfact. Ας προσεχθεί εδώ, ότι επειδή ζητείται γινόμενο, η αρχική τιμή του nfact είναι 1.

Με τον ίδιο τρόπο που καλείται ο αλγόριθμος Παραγοντικό από τον αλγόριθμο Συνδυασμοί, μπορεί να κληθεί και ο τελευταίος από έναν άλλο αλγόριθμο, όπως π.χ. τον επόμενο.

Αλγόριθμος Τράπουλα

Εμφάνισε ''Αριθμός Φύλλων:''

Διάβασε fylla

deck ← 52

Κάλεσε Συνδυασμοί(deck, fylla, number)

Εμφάνισε ''Οι συνδυασμοί'', deck, ''φύλλων ανά'', fylla, ''είναι:'', number

Τέλος Τράπουλα

2η

ENOTHTA

Θέματα Θεωρητικής
Επιστήμης των Υπολογιστών

Η εντολή Κάλεσε συνοδεύεται με το όνομα του καλούμενου αλγορίθμου ακολουθούμενο πιθανά από λίστα μεταβλητών ή σταθερών μέσα σε παρενθέσεις. Οι τιμές των μεταβλητών ή σταθερών μεταβιβάζονται κατά την κλήση στις αντίστοιχες μεταβλητές της γραμμής Δεδομένα του καλούμενου αλγορίθμου. Όταν ο καλούμενος αλγόριθμος τερματίσει τη λειτουργία του, γίνεται επιστροφή στην αμέσως επόμενη εντολή της Κάλεσε. Κατά την επιστροφή μπορεί επίσης να μεταβιβάζονται τιμές της εντολής Αποτελέσματα.

Οι συνδυασμοί απαντούν στο ερώτημα κατά πόσους διαφορετικούς τρόπους είναι δυνατό π.χ. να εξαχθούν 5 φύλλα από μια τράπουλα των 52 φύλλων.

Ο αλγόριθμος Παραγοντικό καλείται τρεις φορές από τον αλγόριθμο Συνδυασμοί. Σε κάθε κλήση μεταβιβάζεται η τιμή του αριθμού για τον οποίον ζητείται το παραγοντικό, στη μεταβλητή n του καλούμενου αλγόριθμου Παραγοντικό. Όταν ο τελευταίος τερματίσει, επιστρέφει το αποτέλεσμα nfact.

Οι μεταβλητές n και nfact του αλγόριθμου Συνδυασμοί δεν έχουν καμία σχέση με τις συνώνυμες μεταβλητές του αλγορίθμου Παραγοντικό.

2.2.7.6 Αναδρομή

Πολλές επιστημονικές εφαρμογές χρησιμοποιούν συναρτήσεις ή σχέσεις γενικότερα που χρησιμοποιούν τις ίδιες στον ορισμό τους. Αυτές οι συναρτήσεις ή σχέσεις ονομάζονται αναδρομικές (Recursive).

Παράδειγμα 2.21. Ν Παραγοντικό

Είδαμε στην παράγραφο 2.2.4 τον αναδρομικό ορισμό του Ν!. Με βάση αυτόν τον ορισμό, παρατίθεται ο αναδρομικός αλγόριθμος υπολογισμού του Ν!.

Αλγόριθμος Ν_Παραγοντικό

Διάβασε Ν

Κάλεσε Factorial (N, N_Fact)

Εμφάνισε Ν, ''!='', N_Fact

Τέλος Ν_Παραγοντικό1

Αλγόριθμος Factorial

Δεδομένα // n //

Aν n > 0 τότε

Κάλεσε Factorial(n - 1, Fact)

Fact ← Fact * n

αλλιώς

Fact ← 1

Τέλος_αν

Αποτελέσματα // Fact //

Τέλος Factorial

Παράδειγμα 2.22. Μέγιστος Κοινός Διαιρέτης

Παρατίθεται εδώ η αναδρομική εκδοχή του αλγόριθμου του Ευκλείδη

Αλγόριθμος Ευκλείδης

Διάβασε α, β

Κάλεσε ΜΚΔ(α, β)

Τέλος Ευκλείδης

Αλγόριθμος ΜΚΔ

Δεδομένα // x, y //

Αν y = 0 τότε

Εμφάνισε x

αλλιώς

x ← x mod y

Κάλεσε ΜΚΔ (y, x)

Τέλος_αν

Τέλος ΜΚΔ

2.2.8 Βασικές αλγοριθμικές λειτουργίες σε δομές δεδομένων

Όπως αναφέρθηκε ήδη, οι δομές δεδομένων διαθέτουν οργανωμένα δεδομένα, στα οποία μπορούν να γίνουν διάφορες επεξεργασίες. Οι βασικές λειτουργίες ή πράξεις επί των δομών δεδομένων είναι οι ακόλουθες:

Προσπέλαση (access), πρόσβαση σε δεδομένα με σκοπό την ανάγνωση ή εγγραφή ή μετακίνηση.
Ανάκτηση (retrieval), η με οποιονδήποτε τρόπο λήψη (ανάγνωση) του περιεχομένου ενός κόμβου.

2.2

ΚΕΦΑΛΑΙΟ

Αλγόριθμοι

Από τη μελέτη του παραδείγματος 2.20 αναδεικνύεται και ο σωστός τρόπος αντιμετώπισης προβλημάτων. Κάθε πρόβλημα διασπάται σε μικρότερα προβλήματα, τα οποία μπορούν να επιλυθούν πιο εύκολα. Ο αλγόριθμος επίλυσης ενός προβλήματος πρέπει να επικεντρώνεται στο πρόβλημα που επιλύει και να αδιαφορεί για το πού θα χρησιμοποιηθεί, καθώς και για την είσοδο και έξοδο των δεδομένων. Με τη χρήση των εντολών Δεδομένα και Αποτελέσματα επιτυγχάνεται πολύ εύκολα η μεταφορά των δεδομένων ενός προβλήματος από/ προς τον αλγόριθμο επίλυσης. Στα επόμενα θα γίνεται αποκλειστική χρήση των εντολών αυτών, εκτός από τις περιπτώσεις που η είσοδος δεδομένων και η έξοδος αποτελεσμάτων είναι το προς επίλυση πρόβλημα.

Στο παράδειγμα αυτό, ο αλγόριθμος Ευκλείδης καλεί τον αλγόριθμο ΜΚΔ μεταβιβάζοντάς του τις τιμές των μεταβλητών α και β στις μεταβλητές x και y αντίστοιχα. O αλγόριθμος ΜΚΔ με την εντολή Κάλεσε καλεί τον εαυτό του δίνοντας άλλες τιμές στις μεταβλητές x και y.

Αναζήτηση (searching) ενός συνόλου στοιχείων δεδομένων προκειμένου να εντοπιστούν ένα ή περισσότερα στοιχεία, που έχουν μια δεδομένη ιδιότητα.
Εισαγωγή (insertion), η προσθήκη ή δημιουργία νέων κόμβων σε μια υπάρχουσα δομή.
Μεταβολή ή τροποποίηση (modification), η αλλαγή του περιεχομένου ενός κόμβου.
Διαγραφή (deletion) ή ακύρωση που συνιστά το αντίθετο της εισαγωγής.
Ταξινόμηση (sorting), όπου τα στοιχεία μιας δομής διατάσσονται κατά αύξουσα ή φθίνουσα τάξη.

Άλλες λειτουργίες είναι η συγχώνευση (merging), κατά την οποία δύο ή περισσότερες ταξινομημένες δομές συνενώνονται σε μια ενιαία δομή, η προσάρτηση (append), κατά την οποία μία δομή επικολλάται στο τέλος μιας άλλης, η αντιγραφή (copying), κ.ά..

Η πιο συνηθισμένη και απλή δομή δεδομένων είναι ο πίνακας. Οι πίνακες υποστηρίζονται από όλες σχεδόν τις γλώσσες προγραμματισμού. Αποτελούνται από ένα σύνολο ομοειδών απλών στοιχείων. Το μέγεθος ενός πίνακα, δηλαδή το πλήθος των στοιχείων που περιέχει, συνήθως είναι σταθερό και προκαθορισμένο. Η αναφορά σε ένα στοιχείο του πίνακα γίνεται με τη χρήση ενός συμβολικού ονόματος που έχει αποδοθεί στον πίνακα, μαζί με ένα ή περισσότερα στοιχεία που ονομάζονται δείκτες (indexes). Για παράδειγμα το πέμπτο στοιχείο του πίνακα Α συμβολίζεται με Α[5].

Στη συνέχεια παρουσιάζονται χαρακτηριστικά παραδείγματα επεξεργασίας πινάκων.

Παράδειγμα 2.23. Εισαγωγή στοιχείων σε πίνακα

➢ Είσοδος δεδομένων αγνώστου πλήθους

Στο επόμενο τμήμα αλγορίθμου εισάγονται θετικοί αριθμοί στο μονοδιάστατο πίνακα Α. Δεν είναι γνωστός ο αριθμός των στοιχείων που θα εισαχθούν, αλλά έχει συμφωνηθεί ότι το τέλος της εισαγωγής θα καθοριστεί από την είσοδο ενός αρνητικού αριθμού (ή γενικότερα μιας τιμής που δεν μπορεί να ανήκει στο σύνολο τιμών του πίνακα).

i ← 0

Διάβασε Κ

Όσο Κ ≥ 0 επανάλαβε

i ← i + 1

A[i] ← K

Διάβασε Κ

Τέλος_επανάληψης

n ← i

2η

ENOTHTA

Θέματα Θεωρητικής
Επιστήμης των Υπολογιστών

Στην πράξη σπάνια υπάρχουν όλες οι λειτουργίες σε μια δομή. Συνήθως παρατηρείται το φαινόμενο μια δομή δεδομένων να είναι αποδοτικότερη από μια άλλη για κάποια λειτουργία π.χ. την αναζήτηση, αλλά λιγότερο αποδοτική για κάποια άλλη λειτουργία, όπως π.χ. την εισαγωγή. Αυτό εξηγεί τόσο την ύπαρξη διαφορετικών δομών όσο και τη σπουδαιότητα της επιλογής της κατάλληλης δομής κάθε φορά.

Οι πίνακες με ένα δείκτη λέγονται μονοδιάστατοι, οι πίνακες με 2 δείκτες δισδιάστατοι, .... οι πίνακες με ν δείκτες ν-διάστατοι.

Εδώ χρησιμοποιείται η εντολή επανάληψης Όσο συνθήκη επανάλαβε. Απαιτεί ένα αρχικό διάβασμα προκειμένου να ενεργοποιηθεί η συνθήκη συνέχισης της επανάληψης. Κάθε θετική τιμή που διαβάζεται καταχωρείται σε επόμενο στοιχείο του πίνακα με τη χρήση του δείκτη i. Στο τέλος φυλάσσεται στη μεταβλητή n η τρέχουσα τιμή του i, ώστε να είναι γνωστό το πλήθος των στοιχείων του πίνακα στη συνέχεια.

➢ Είσοδος δεδομένων γνωστού πλήθους

Όταν είναι γνωστό το πλήθος n των τιμών μπορεί να χρησιμοποιηθεί η εντολή επανάληψης Για … από …μέχρι. Η πιο απλή εκδοχή είναι η επόμενη.

Για i από 1 μέχρι n

Διάβασε Α[i]

Τέλος_επανάληψης

Σε όλες τις προηγούμενες περιπτώσεις εισαγωγής τιμών σε πίνακα, ο χρήστης του σχετικού προγράμματος μπορεί να υποβοηθείται με την εμφάνιση κατάλληλων μηνυμάτων.

Παράδειγμα 2.24. Εκτύπωση πίνακα

Η εκτύπωση των στοιχείων του πίνακα, καθώς και της θέσης που υπάρχει το στοιχείο, επιτυγχάνεται με τις επόμενες εντολές:

Για i από 1 μέχρι n

Εμφάνισε i, Α[i]

Τέλος_επανάληψης

Παράδειγμα 2.25. Τροποποίηση στοιχείων πίνακα

Μετά την εισαγωγή στοιχείων και την εκτύπωση μπορεί να απαιτείται η διόρθωση ενός ή περισσοτέρων στοιχείων.

Διάβασε i

Όσο i > 0 και i <= n επανάλαβε

Εμφάνισε Α[i]

Διάβασε Α[i]

Διάβασε i

Τέλος_επανάληψης

Στον αλγόριθμο αυτό η επανάληψη εκτελείται όσο δίνεται τιμή του i εντός ορίων. Κάθε φορά εμφανίζεται το στοιχείο Α[i] και ζητείται η εισαγωγή μιας άλλης τιμής που την αντικαθιστά.

Μετά την εισαγωγή δεδομένων σε ένα πίνακα μπορεί να ακολουθήσει η επεξεργασία του. Στη συνέχεια παρουσιάζονται μερικές συνηθισμένες επεξεργασίες πινάκων.

Παράδειγμα 2.26. Άθροισμα στοιχείων πίνακα

Δίδεται ο μονοδιάστατος πίνακας Β που περιέχει Ν βαθμούς μαθητών. Να αναπτυχθεί αλγόριθμος, ο οποίος να υπολογίζει και να εμφανίζει το μέσο όρο βαθμολογίας των μαθητών.

2.2

ΚΕΦΑΛΑΙΟ

Αλγόριθμοι

Πριν από κάθε επεξεργασία πίνακα απαιτείται να εισαχθούν δεδομένα σε αυτόν. Η εισαγωγή δεδομένων σε πίνακα μπορεί να είναι επίπονη διαδικασία, ιδιαίτερα αν ο πίνακας είναι μεγάλος. Επί πλέον τα λάθη πληκτρολόγησης είναι πολύ συνηθισμένα και πρέπει να υπάρχει τρόπος διόρθωσης κάποιων τιμών.

Αλγόριθμος Βαθμολογία

Δεδομένα // Β, Ν //

Σ ← 0

Για i από 1 μέχρι Ν

Σ ← Σ + Β[i]

Τέλος_επανάληψης

ΜΟ ← Σ / Ν

Εμφάνισε ''Μ.Ο.:'', ΜΟ

Τέλος Βαθμολογία

Με το βρόχο Για i από 1 μέχρι Ν διατρέχονται όλα τα στοιχεία του πίνακα και κάθε ένα αθροίζεται στη μεταβλητή Σ, η οποία έχει μηδενιστεί πριν από την έναρξη της επανάληψης. Ο Μέσος όρος είναι το πηλίκο του αθροίσματος όλων των στοιχείων δια του πλήθους των στοιχείων.

Για τη δημιουργία προγράμματος που να υλοποιεί τον παραπάνω αλγόριθμο και προκειμένου να γίνει ο έλεγχος ορθότητας, απαιτείται και η εισαγωγή κάποιων δεδομένων. Σύμφωνα με όσα αναφέρθηκαν στις προηγούμενες παραγράφους αυτό μπορεί να γίνει π.χ. με τον επόμενο αλγόριθμο.

Αλγόριθμος Επεξεργασία_Πίνακα

Διάβασε n

Για i από 1 μέχρι n

Διάβασε Α[i]

Τέλος_επανάληψης

Κάλεσε Βαθμολογία (Α, n)

Τέλος Επεξεργασία_Πίνακα

Στις πρώτες γραμμές έχουν γραφεί οι σχετικές εντολές με τις οποίες γίνεται η εισαγωγή δεδομένων στο μονοδιάστατο πίνακα Α, ο οποίος έχει n στοιχεία. Στη συνέχεια προκειμένου να βρεθεί ο μέσος όρος των στοιχείων του Α, καλείται ο αλγόριθμος Βαθμολογία, που δημιουργήθηκε για το σκοπό αυτό. Κατά την κλήση μεταβιβάζονται στον πίνακα Β οι τιμές των στοιχείων του πίνακα Α και στη μεταβλητή Ν η τιμή της μεταβλητής n.

Παράδειγμα 2.27. Μέγιστο στοιχείο πίνακα

Δίδεται ο μονοδιάστατος πίνακας Β που περιέχει Ν βαθμούς μαθητών. Να αναπτυχθεί αλγόριθμος, ο οποίος να βρίσκει και να εμφανίζει την υψηλότερη βαθμολογία.

Αλγόριθμος Μέγιστο_πίνακα

Δεδομένα // Β, Ν //

max ← Β[1]

Για i από 2 μέχρι Ν

Αν Β[i] > max τότε

max ← Β[i]

Τέλος_αν

Τέλος_επανάληψης

Εμφάνισε ''Μέγιστο:'', max

Τέλος Μέγιστο_πίνακα

Στη μεταβλητή max εκχωρείται η τιμή του πρώτου στοιχείου του πίνακα. Στη συνέχεια με το βρόχο Για i από 2 μέχρι Ν εξετάζονται όλα τα υπόλοιπα στοιχεία του πίνακα. Για κάθε ένα, αν είναι μεγαλύτερο από το max, τότε αντικαθιστάται η τιμή του max με το νέο στοιχείο. Δηλαδή στη μεταβλητή max εκχωρείται το εκάστοτε μέγιστο στοιχείο, οπότε στο τέλος της επανάληψης θα έχει το μέγιστο στοιχείο του πίνακα.

2η

ENOTHTA

Θέματα Θεωρητικής
Επιστήμης των Υπολογιστών

Η επανάληψη θα μπορούσε
να ξεκινά από 1.

Παράδειγμα 2.28. Επεξεργασία δισδιάστατου πίνακα

Να αναπτυχθεί αλγόριθμος ο οποίος με δεδομένο το πλήθος των μαθητών της Γ’ γυμνασίου ενός σχολείου και τους βαθμούς των μαθητών στη γυμναστική, σε καθένα από τα 3 τρίμηνα, να υπολογίζει και να επιστρέφει το μέσο όρο βαθμολογίας κάθε μαθητή και το συνολικό μέσο όρο.

Ο πίνακας Β έχει Ν γραμμές και 3 στήλες. Σε κάθε μία γραμμή υπάρχουν οι βαθμολογίες των τριών τριμήνων για κάθε ένα μαθητή.

Αλγόριθμος Αθροίσματα

Δεδομένα // Β, Ν //

Σ ← 0

Για i από 1 μέχρι Ν

ΣΜ ← 0

Για j από 1 μέχρι 3

ΣΜ ← ΣΜ + Β[i, j]

Τέλος_επανάληψης

ΜΟΒ[i]← ΣΜ / 3

Σ ← Σ + ΣΜ

Τέλος_επανάληψης

ΜΟ ← Σ / (Ν * 3)

Αποτελέσματα // ΜΟΒ, ΜΟ //

Τέλος Αθροίσματα

Με το διπλό βρόχο Για i και Για j σαρώνονται κατά γραμμή όλα τα στοιχεία του πίνακα Β. Σε κάθε μία γραμμή, δηλαδή για κάθε μία τιμή του i, μηδενίζεται το ΣΜ (άθροισμα βαθμών μαθητή) και ακολούθως με τον εσωτερικό βρόχο αθροίζονται όλα τα στοιχεία της γραμμής αυτής. Όταν ολοκληρωθεί ο εσωτερικός βρόχος, στο ΜΟΒ[i] βρίσκεται ο μέσος όρος των στοιχείων της εκάστοτε γραμμής, δηλαδή ο μέσος όρος κάθε μαθητή στα τρία τρίμηνα. Το άθροισμα που υπολογίστηκε ανά γραμμή αξιοποιείται και αυξάνει τη μεταβλητή Σ κατά το άθροισμα γραμμής, η οποία στο τέλος θα έχει το άθροισμα όλων των στοιχείων του πίνακα.

Παράδειγμα 2.29. Σειριακή αναζήτηση

Σε ένα μονοδιάστατο πίνακα είναι καταχωρημένα τα ονόματα των σχολείων που συμμετέχουν σε έναν διαγωνισμό επιχειρηματικότητας και έχουν κατασκευάσει ένα χώρο παρουσίασης του επιχειρηματικού τους σχεδίου (που εν συντομία θα λέγεται περίπτερο). Ο αριθμός του περιπτέρου κάθε σχολείου είναι η θέση του σχολείου στον πίνακα. Δηλαδή στο πρώτο κελί του πίνακα είναι το όνομα του σχολείου που έχει το περίπτερο με αριθμό 1, στο δεύτερο κελί του πίνακα είναι το όνομα του σχολείου που έχει το περίπτερο με αριθμό 2 κ.ο.κ. Να αναπτυχθεί αλγόριθμος ο οποίος με δεδομένο το πλήθος των σχολείων που συμμετέχουν στο διαγωνισμό με περίπτερο και τον πίνακα με τα ονόματα των σχολείων, να διαβάζει το όνομα ενός σχολείου και να ψάχνει στον πίνακα, αν υπάρχει αυτό το σχολείο. Ο αλγόριθμος θα επιστρέφει το αποτέλεσμα της αναζήτησης, δηλαδή αν υπάρχει ή όχι το αναζητούμενο σχολείο, και αν υπάρχει τη θέση του στον πίνακα, αλλιώς ως θέση την τιμή μηδέν.

Αλγόριθμος Αναζήτηση

Δεδομένα // Α, Ν //

Εμφάνισε ''Αναζητούμενο σχολείο:''

Διάβασε Κ

i ← 1

Βρέθηκε ← Ψευδής

Θέση ← 0

2.2

ΚΕΦΑΛΑΙΟ

Αλγόριθμοι

Για την εισαγωγή δεδομένων σε ένα δισδιάστατο πίνακα Α που έχει Ν γραμμές και Μ στήλες, θα μπορούσε να αναπτυχθεί το ακόλουθο τμήμα αλγορίθμου:

Για i από 1 μέχρι Ν

Για j από 1 μέχρι Μ

Διάβασε Α[i, j]

Τέλος_επανάληψης

Ο αλγόριθμος αθροίζει τα στοιχεία κάθε γραμμής ενός δισδιάστατου πίνακα Ν γραμμών και 3 στηλών.

Ο μέσος όρος είναι το πηλίκο του αθροίσματος δια του πλήθους των στοιχείων του δισδιάστατου πίνακα. Το πλήθος των στοιχείων του είναι Ν*3.

Κάθε σχολείο μπορεί να έχει ένα περίπτερο.

Στον αλγόριθμο είναι δεδομένος ο πίνακας Α και το πλήθος των στοιχείων του (Ν).

Η λογική μεταβλητή Βρέθηκε έχει την αρχική τιμή Ψευδής, όπου θεωρείται ότι δεν υπάρχει το ζητούμενο σχολείο και η μεταβλητή Θέση έχει την αρχική τιμή 0 για τον ίδιο λόγο.

Η επανάληψη του αλγορίθμου εκτελείται όσο δεν τελείωσε η σάρωση του πίνακα (i ≤ Ν) και όσο δεν βρέθηκε το στοιχείο (Βρέθηκε = Ψευδής).

Όσο i ≤ Ν και Βρέθηκε = Ψευδής επανάλαβε

Αν Κ = Α[i] τότε

Θέση ← i

Βρέθηκε ← Αληθής

αλλιώς

i ← i + 1

Tέλος_αν

Τέλος_επανάληψης

Αποτελέσματα // Βρέθηκε, Θέση //

Τέλος Αναζήτηση

Τα αποτελέσματα είναι η μεταβλητή Βρέθηκε, η οποία, αν είναι αληθής σημαίνει ότι η αναζήτηση ήταν επιτυχής και η μεταβλητή Θέση, που έχει τη θέση του στοιχείου στον πίνακα, εφ’ όσον βρέθηκε, αλλιώς θα έχουν την τιμή Ψευδής και μηδέν αντίστοιχα. Η τιμή μηδέν δεν μπορεί να είναι θέση πίνακα.

Παράδειγμα 2.30. Ταξινόμηση με επιλογή

Να αναπτυχθεί αλγόριθμος ο οποίος με δεδομένο το πλήθος των μαθητών της Γ’ γυμνασίου ενός σχολείου και τον τελικό βαθμό του κάθε μαθητή στο μάθημα «Πληροφορική», να ταξινομεί τον πίνακα των βαθμών σε αύξουσα τάξη, από το μικρότερο στο μεγαλύτερο βαθμό. Στη συνέχεια να επιστρέφει τον ταξινομημένο πίνακα.

Αλγόριθμος Ταξινόμηση_με_επιλογή

Δεδομένα // A, N //

Για i από 1 μέχρι Ν

j ← i

min ← A[j]

Για k από i + 1 μέχρι Ν

Αν A[k] < min τότε

j ← k

min ← A[j]

Τέλος_αν

Τέλος_επανάληψης

temp ← A[i]

A[i] ← A[j]

A[j] ← temp

Τέλος_επανάληψης

Αποτελέσματα // Α //

Τέλος Ταξινόμηση_με_επιλογή

2.2.9 Εκσφαλμάτωση σε λογικά λάθη

Ένας αλγόριθμος χρειάζεται να δοκιμαστεί σε διαφορετικές συνθήκες και με ποικιλία δεδομένων ώστε να συγκριθούν τα παραγόμενα αποτελέσματα με τα αναμενόμενα, και να προβλεφτούν απρόσμενες καταστάσεις λάθους.

2η

ENOTHTA

Θέματα Θεωρητικής
Επιστήμης των Υπολογιστών

Εικόνα 2.24. Σειριακή αναζήτηση.

Η μέθοδος της ταξινόμησης με επιλογή βασίζεται στα ακόλουθα τρία βήματα:

α. επιλογή του στοιχείου με την ελάχιστη τιμή.
β. ανταλλαγή του με το πρώτο στοιχείο.
γ. επανάληψη των (α), (β) με τα υπόλοιπα στοιχεία.

Ο αλγόριθμος ταξινόμησης με επιλογή είναι πολυπλοκότητας Ο(n2)

Ως εκσφαλμάτωση των λογικών λαθών ενός αλγορίθμου προσδιορίζεται η διαδικασία εύρεσης των λογικών λαθών που υπάρχουν σε αυτόν.

Η ανίχνευση τέτοιων λαθών δεν είναι δυνατό να πραγματοποιηθεί από κάποιο εργαλείο του υπολογιστή και διαπιστώνονται μόνο με τη διαδικασία ελέγχου και την ανάλυση των αποτελεσμάτων του. Ένα λογικό λάθος είναι ένα λάθος που, ενώ εκτελείται ο αλγόριθμος, τα αποτελέσματά του δεν είναι σωστά. Αυτό μπορεί να οφείλεται είτε σε λανθασμένη προσέγγιση για το πώς θα λυθεί το πρόβλημα, είτε σε λανθασμένη υλοποίηση της προσέγγισης που επιλέχθηκε. Κατά γενική ομολογία, τα λογικά λάθη είναι δύσκολο να εντοπιστούν.

Παράδειγμα 2.31. Λανθασμένος αλγόριθμος

Με σκοπό να αναπτυχθεί αλγόριθμος ο οποίος με δεδομένες τις τιμές δύο μεταβλητών, θα αντιμεταθέτει το περιεχόμενο των δύο μεταβλητών και θα επιστρέφει ως αποτέλεσμα το περιεχόμενο των μεταβλητών μετά την αντιμετάθεση γράφτηκε ο ακόλουθος λανθασμένος αλγόριθμος σε ψευδογλώσσα. Ζητείται να εντοπιστούν τα λογικά λάθη.

Αλγόριθμος Αντιμετάθεση
Δεδομένα // α, β //
α ← β
β ← α
Αποτελέσματα // α, β //
Τέλος Αντιμετάθεση

Απάντηση

Το πρώτο βήμα είναι η εκτέλεση του αλγορίθμου με πίνακα παρακολούθησης τιμών για να ελεγχθεί η λειτουργία του.

Αριθμός Εντολής	α	β	Έξοδος
2	8	12
3	12
4		12
5			12 12

Από την εκτέλεση φαίνεται ότι εκτυπώνει σωστά την τιμή της μεταβλητής α, αλλά όχι της β. Αφού διαπιστωθεί το λάθος χρειάζεται να προσδιοριστεί η απαιτούμενη διόρθωση. Από τον αλγόριθμο απουσιάζει η μεταβλητή στην οποία θα εκχωρούταν προσωρινά η τιμή μίας εκ των δύο μεταβλητών.

2.2

ΚΕΦΑΛΑΙΟ

Αλγόριθμοι

Το πρώτο βήμα στην εύρεση των λογικών λαθών είναι να γίνει προσπάθεια εντοπισμού των πιθανών πηγών τους. Για να επιτευχθεί αυτό χρειάζεται να δώσετε προσοχή στα αποτελέσματα που έχει ως έξοδο ο αλγόριθμος και να σκεφτείτε πιθανές αιτίες που μπορεί να οδήγησαν σε τέτοιου είδους αποτελέσματα.

Η εκτέλεση του αλγορίθμου με το χέρι είναι πολύ χρήσιμη διαδικασία για τον εντοπισμό των λογικών λαθών.

Για το λόγο αυτό χρειάζεται να δοκιμάζετε εξονυχιστικά τον αλγόριθμό σας με διάφορα παραδείγματα, απλά, σύνθετα και ασυνήθιστα, για να βεβαιωθείτε ότι είναι σωστός.

Αν κάποιο από τα παραδείγματα δεν δίνει το αναμενόμενο αποτέλεσμα τότε υπάρχει παράλειψη στον κώδικα και δεν έχει καλυφθεί η σχετική περίπτωση.

Μόλις βρείτε τι φταίει, εμπλουτίζετε την αρχική σας σχεδίαση ώστε να καλύψετε και αυτό το είδος περιπτώσεων και κάνετε τις απαραίτητες προσθήκες.

Η διαδικασία εκσφαλμάτωσης περιλαμβάνει:

Τη διαπίστωση του είδους του λάθους.
Την ανεύρεση του ανεξάρτητου τμήματος του αλγορίθμου που εκτελεί τη λανθασμένη λειτουργία.
Την ανεύρεση του λάθους μέσα σε αυτό το ανεξάρτητο τμήμα του αλγορίθμου.

2.2.10 Τεκμηρίωση

Η τεκμηρίωση δεν αποτελεί μια ξεχωριστή φάση στην ανάπτυξη ενός αλγορίθμου, αλλά μία παράλληλη διαδικασία που συμπληρώνει όλα τα στάδια ανάπτυξής του.

Με τον όρο τεκμηρίωση εννοείται το σύνολο του γραπτού υλικού που περιγράφει τα συστατικά μέρη και τις λειτουργίες του αλγορίθμου ή τις τροποποιήσεις που έγιναν σε έναν αλγόριθμο.

Τεκμηρίωση ανάπτυξης. Αναφέρεται στις προδιαγραφές του προβλήματος, τι πρόκειται να κάνει ο αλγόριθμος και τη σύνδεσή του με άλλους αλγορίθμους.
Τεκμηρίωση ελέγχου. Αναφέρεται στα δεδομένα ελέγχου που χρησιμοποιήθηκαν προκειμένου να δοκιμαστεί ο αλγόριθμος, αν έχουν διερευνηθεί οι ακραίες περιπτώσεις και ποιες είναι αυτές και τέλος αν έχουν καθιερωθεί κάποιες και ποιες συμβάσεις για τη λύση του προβλήματος.
Τεκμηρίωση αλγορίθμου. Αναφέρεται στον τρόπο με τον οποίο έχουν λυθεί τα επιμέρους προβλήματα, τις υποθέσεις που έχουν γίνει και τους περιορισμούς που έχουν τεθεί. Ακόμα πληροφορίες για «ειδικές» τεχνικές που έχουν χρησιμοποιηθεί. Πρέπει σε κάθε βήμα να αναφερθεί με λεπτομέρεια, πολλές φορές κουραστική, αλλά δυστυχώς αναγκαία, η λύση που χρησιμοποιήθηκε και τα δεδομένα με τα οποία ελέγχθηκε. Ένα υπόμνημα των μεταβλητών που χρησιμοποιούνται είναι χρήσιμο για την τεκμηρίωση αλλά και για την αρχική ανάπτυξη του αλγόριθμου.

Η απλούστερη και πλέον στοιχειώδης τεκμηρίωση αυτής της μορφής γίνεται με την εισαγωγή γραμμών σχολίων μέσα στον αλγόριθμο.

Ανακεφαλαίωση

Στις παραγράφους του κεφαλαίου παρουσιάστηκαν η έννοια του αλγορίθμου μαζί με τα χαρακτηριστικά που χρειάζεται να έχει, οι τρόποι παράστασης αλγορίθμων, τα συστατικά τους μέρη, οι δομές δεδομένων και διατυπώθηκαν βασικά στοιχεία ανάλυσης και θεωρίας αλγορίθμων. Επιπλέον, παρουσιάστηκε η ψευδογλώσσα ως βασικότερος τρόπος ανάπτυξης αλγορίθμων, προκειμένου να υπάρχει ανεξαρτησία από τις γλώσσες προγραμματισμού. Παρουσιάστηκαν πολλά παραδείγματα απλών αλγορίθμων, ενώ αναπτύχθηκαν αλγόριθμοι αναζήτησης και ταξινόμησης. Τέλος, στο κεφάλαιο αυτό, επιχειρήθηκε να αναδειχθεί ότι οι αλγόριθμοι και οι δομές δεδομένων έχουν ισχυρότατη σχέση και αποτελούν τα βασικά συστατικά για την ανάπτυξη προγραμμάτων.

2η

ENOTHTA

Θέματα Θεωρητικής
Επιστήμης των Υπολογιστών

Οι λόγοι τεκμηρίωσης είναι:

η ευκολία ανάπτυξης αλγορίθμου σε περίπτωση που ζητείται αλγόριθμος με παρόμοιες λειτουργίες με υπάρχοντα αλγόριθμο.
Η ευκολία στις τροποποιήσεις ενός υπάρχοντος αλγορίθμου.
Ο περιορισμός των ελέγχων μόνο σε συγκεκριμένα σημεία, αφού για τα υπόλοιπα θα υπάρχει αρχείο δοκιμής μαζί με αποτελέσματα και συνοδευτικά σχόλια.

Λέξεις κλειδιά

Αλγόριθμος, Χαρακτηριστικά αλγορίθμου, Ψευδογλώσσα, Διάγραμμα ροής, Μεταβλητές, Εκφράσεις, Εντολή εκχώρησης, Δομή ακολουθίας, Δομή επιλογής, Δομή επανάληψης, Δομές δεδομένων, Πίνακας, Ουρά, Στοίβα, Γράφος, Δένδρο, Αναζήτηση, Ταξινόμηση, Εκσφαλμάτωση, Τεκμηρίωση.

2.2

ΚΕΦΑΛΑΙΟ

Ερωτήσεις - Θέματα προς συζήτηση - Δραστηριότητες

Τι είναι αλγόριθμος; Καταγράψτε ή συζητήστε με τους συμμαθητές σας έναν αλγόριθμο.
Μέσα από παιχνίδι ρόλων να υλοποιήσετε και να εκτελέσετε τον αλγόριθμο του παραδείγματος 2.5 σειριακά και παράλληλα.
Με ποιους τρόπους γίνεται η αναπαράσταση αλγορίθμων;
Ποια η διαφορά δεδομένου και πληροφορίας; Να δώσετε ένα παράδειγμα.
Ποιοι είναι οι συνηθέστεροι τύποι δεδομένων; Ποιος τύπος λαμβάνει τις λιγότερες τιμές;
Τι είναι η δομή δεδομένων;
Ποιες δομές δεδομένων είναι μη γραμμικές;
Ποια είναι τα είδη των τελεστών;
Ποια είναι η χρήση της δομής ακολουθίας; Να δώσετε έναν αλγόριθμο σε ψευδογλώσσα με τη χρήση της δομής ακολουθίας.
Να περιγράψετε τη λειτουργία των τριών εντολών επιλογής.
Να περιγράψετε τη λειτουργία των τριών εντολών επανάληψης.
Να εξηγήσετε πότε δεν μπορεί να χρησιμοποιηθεί η εντολή επανάληψης Για.
Ποιες είναι οι λειτουργίες ή πράξεις επί των δομών δεδομένων;
Να περιγράψετε τον αλγόριθμο ταξινόμησης επιλογής σε πίνακα.
Σημειώστε τις σωστές απαντήσεις
- Α. Ποια από τα παρακάτω αποτελούν αριθμητική σταθερά;
  1. 2009
  2. ''2009''
  3. Εμφάνισε
  4. ''Αλγόριθμος''
- Β. Η λογική πράξη ή μεταξύ δύο προτάσεων είναι αληθής όταν:
  1. Οποιαδήποτε από τις προτάσεις είναι αληθής
  2. Η πρώτη πρόταση είναι αληθής
  3. Η πρώτη πρόταση είναι ψευδής
  4. Και οι δύο προτάσεις είναι αληθείς
- Γ. Αν Α και Β ακέραιες μεταβλητές, ποιες από τις παρακάτω εκφράσεις είναι αριθμητικές;
  1. Α + Β ^ 2
  2. Α > Β + 3
  3. Α div 3 ^ Β
  4. Α και Β > 3
Να μετατρέψετε σε εντολές εκχώρησης τις παρακάτω φράσεις:
- Α. Η μεταβλητή α έχει διπλάσια τιμή από τη μεταβλητή β
- Β. Η μεταβλητή ΜΟ είναι ο μέσος όρος των α, β, γ
- Γ. Η μεταβλητή β αυξάνεται κατά 2
- Δ. Η μεταβλητή i μειώνεται κατά α και β
- Ε. Η μεταβλητή i είναι το μισό του αθροίσματος των α και β

Να επιλέξετε την τιμή της y που είναι αποτέλεσμα κάθε εντολής.

Εντολές εκχώρησης	Τιμή της y
i. y←(A_M(7 / 2) mod 3) + 1 ii. y←10 div 9 - 10 mod 9 iii. y ←10 mod 2 + Α_Τ(2 - 3) iv. y ←Α_Μ(9 / 2 / 3)	A. 1 B. 0

Εντολές εκχώρησης

Τιμή της y

i. y←(A_M(7 / 2) mod 3) + 1

ii. y←10 div 9 - 10 mod 9

iii. y ←10 mod 2 + Α_Τ(2 - 3)

iv. y ←Α_Μ(9 / 2 / 3)

A. 1

B. 0

Αντιστοιχίστε τις εκφράσεις της στήλης Α με τις λογικές σταθερές της στήλης Β με δεδομένο ότι α = 10, β = 5 και γ = 3.

Στήλη Α	Στήλη Β
i. α ≠ β και (γ - β) < 0 ii. (α > β ή α > γ) και (γ > β) iii. α > β ή α > γ και γ > β iv. όχι (α > β) ή γ ≤ β v. α > β ή (β - γ) > 0 και α < 0 vi. α > β ή (β + 3) < γ και α < γ	Α. Αληθής Β. Ψευδής

Στήλη Α

Στήλη Β

i. α ≠ β και (γ - β) < 0

ii. (α > β ή α > γ) και (γ > β)

iii. α > β ή α > γ και γ > β

iv. όχι (α > β) ή γ ≤ β

v. α > β ή (β - γ) > 0 και α < 0

vi. α > β ή (β + 3) < γ και α < γ

Α. Αληθής

Β. Ψευδής

Τι εμφανίζουν τα επόμενα τμήματα αλγορίθμων;

S ← 0

i ← 1

Όσο i ≤ 9 επανάλαβε

    i ← i + 2

    S ← S + i

Τέλος_επανάληψης

Εμφάνισε S

S ← 0

i ← 1

Όσο i ≤ 9 επανάλαβε

    S ← S + i

    i ← i + 2

Τέλος_επανάληψης

Εμφάνισε S
Ο νόμος του Νεύτωνα για τη βαρύτητα λέει ότι κάθε σώμα στο σύμπαν έλκει κάθε άλλο σώμα με δύναμη που δίνεται από τον τύπο,

2η

ΕΝΟΤΗΤΑ

F = G •

m1 • m2 / r²

όπου m1 και m2 είναι οι μάζες των δύο σωμάτων (σε κιλά), r η απόσταση μεταξύ τους (σε μέτρα) και G είναι η παγκόσμια βαρυτική σταθερά. Να αναπτύξετε αλγόριθμο ο οποίος θα διαβάζει τις δύο μάζες, την απόσταση μεταξύ τους και θα υπολογίζει και θα εκτυπώνει τη δύναμη. Δίνεται ότι G = 6,67 x 10-11 N m2 kg-2.
Στην περίοδο των εκπτώσεων αγοράσατε ένα ποδήλατο με έκπτωση 25%. Το ποσό που δώσατε για το ποδήλατο ήταν 100 ευρώ. Να αναπτύξετε αλγόριθμο ο οποίος θα υπολογίζει την αρχική τιμή του ποδηλάτου.
Να αναπτύξετε αλγόριθμο ο οποίος θα διαβάζει έναν αριθμό και θα υπολογίζει και θα εμφανίζει το γινόμενο αυτού του αριθμού επί το τελευταίο ψηφίο του. Θεωρήστε ότι ο αριθμός είναι θετικός και ακέραιος.
Να αναπτύξετε αλγόριθμο ο οποίος θα διαβάζει έναν πραγματικό αριθμό με 2 δεκαδικά ψηφία και θα τον στρογγυλοποιεί στον πλησιέστερο ακέραιο. Για παράδειγμα, αν διαβαστεί ο αριθμός 4,23, να εμφανίζει 4, ενώ αν είναι ο 4,70 να εμφανίζει 5.
Να αναπτύξετε αλγόριθμο ο οποίος θα διαβάζει έναν ακέραιο αριθμό και θα υπολογίζει και θα εμφανίζει τον επόμενο άρτιο.

Σε έναν λογαριασμό τραπέζης παρέχεται κλιμακωτά το ακόλουθο επιτόκιο:

Ποσό	Επιτόκιο
≤ 5.000	1,8% το έτος
> 5.000	1,5% το έτος

Να αναπτύξετε αλγόριθμο ο οποίος θα διαβάζει το ποσό χρημάτων που έχει ο λογαριασμός και θα υπολογίζει και θα εμφανίζει τον τόκο που θα λάβει μετά από ένα έτος, καθώς και το συνολικό ποσό χρημάτων μαζί με τον τόκο.

Να αναπτύξετε αλγόριθμο ο οποίος θα διαβάζει το τρέχον έτος και αν αυτό είναι από το 2001 μέχρι και το 2099 να εμφανίζει το μήνυμα «21ος αιώνας». Αν το έτος είναι από το 2002 και πάνω, να εμφανίζει το μήνυμα «Χρήση του €».
Ένα επιστημονικό σωματείο έχει 1.200 μέλη. Η γενική συνέλευση του σωματείου είναι σε απαρτία όταν είναι παρόν το 1/3 των μελών του. Για να υπερψηφιστεί μια πρόταση, θα πρέπει περισσότεροι από το 1/2 των παρόντων μελών να ψηφίσουν υπέρ. Να αναπτύξετε αλγόριθμο ο οποίος θα διαβάζει τον αριθμό των παρόντων μελών και αν ο αριθμός επιτρέπει την πραγματοποίηση της ψηφοφορίας, θα διαβάζει τον αριθμό αυτών που ψήφισαν υπέρ της πρότασης και θα εμφανίζει το αποτέλεσμα της ψηφοφορίας, δηλαδή αν υπερψηφίστηκε, αν καταψηφίστηκε ή αν δεν μπορεί να ψηφιστεί.

Ένας συνδρομητής μιας εταιρείας κινητής τηλεφωνίας έχει επιλέξει ένα πρόγραμμα με πάγιο 50 ευρώ τον μήνα. Στο πρόγραμμα δικαιούται τις ακόλουθες παροχές:

Παροχές	Πλήθος
Λεπτά ομιλίας/μήνα	1.000
SMS/μήνα	1.000
MB/μήνα	1.000

Ωστόσο, αν ξεπεράσει τον αριθμό 1.000 σε κάποια από τις παραπάνω παροχές, τότε χρεώνεται ως εξής για κάθε παροχή που ξεπερνάει τα 1.000:

Επιπλέον	Πλήθος
Κλήσεις ομιλίας	0,0055 €/δευτερόλεπτο
SMS	0,08 €/SMS
MB	0,05 €/MB

Να αναπτύξετε αλγόριθμο ο οποίος θα διαβάζει τα λεπτά ομιλίας, το πλήθος των SMS, το πλήθος των MB και ανάλογα θα εμφανίζει τη μηνιαία χρέωση του καταναλωτή.

Να αναπτύξετε αλγόριθμο ο οποίος θα εκτυπώνει τις τιμές της συνάρτησης f(x)=4log(5+e3x + 2) όταν το x παίρνει τις τιμές στο διάστημα [10, 50] με βήμα 0,5.
Να αναπτύξετε αλγόριθμο ο οποίος θα εμφανίζει όλους τους τριψήφιους αριθμούς που το άθροισμα των ψηφίων τους είναι μεγαλύτερο ή ίσο του 12.
Να αναπτύξετε αλγόριθμο ο οποίος θα υπολογίζει το ημίτονο ενός αριθμού x με βάση

2.2

ΚΕΦΑΛΑΙΟ

τον επόμενο τύπο

Να αναπτύξετε αλγόριθμο ο οποίος θα διαβάζει γράμματα μέχρι να βρει τρεις φορές το γράμμα Α. Όταν σταματήσει το διάβασμα γραμμάτων, ο αλγόριθμος θα εκτυπώνει πόσα συνολικά γράμματα διαβάστηκαν.
Να αναπτύξετε αλγόριθμο ο οποίος θα διαβάζει αριθμούς, μέχρι να διαβαστεί ο αριθμός μηδέν. Ο αλγόριθμος θα εκτυπώνει το άθροισμα και το πλήθος των αριθμών που δόθηκαν και ήταν μεγαλύτεροι του 50.
Ένα ψηφιακό φωτογραφικό άλμπουμ έχει αποθηκευτικό χώρο Ν Μbytes. Να αναπτύξετε αλγόριθμο ο οποίος θα διαβάζει το μέγεθος της κάθε φωτογραφίας που επιχειρείται να αποθηκευτεί στο άλμπουμ, μέχρι το άλμπουμ να μη χωράει άλλη φωτογραφία. Ο αλγόριθμος θα επαναλαμβάνεται και θα σταματά αν το μέγεθος της φωτογραφίας που προσπαθεί κάποιος να αποθηκεύσει είναι μεγαλύτερο από τον διαθέσιμο χώρο του άλμπουμ. Όταν η εισαγωγή φωτογραφιών σταματήσει, ο αλγόριθμος θα εκτυπώνει το μήνυμα «Δεν χωράει». Στην περίπτωση που περίσσεψε χώρος να τον εκτυπώνει. Τέλος, να εκτυπώνει το πλήθος των φωτογραφιών που αποθηκεύτηκαν.
Τροποποιείστε τον αλγόριθμο του παραδείγματος 2.26, ώστε να βρίσκει το γινόμενο των στοιχείων του πίνακα.
Να αναπτύξετε αλγόριθμο ο οποίος:
- Α. Θα διαβάζει το πλήθος των μαθητών ενός λυκείου.
- Β. Θα διαβάζει το μέσο όρο βαθμολογίας κάθε μαθητή ο οποίος θα εισάγεται σε πίνακα. Ο μέσος όρος βαθμολογίας κάθε μαθητή θα πρέπει να ελέγχεται ώστε να είναι μεγαλύτερος ή ίσος του (ένα) 1 και μικρότερος ή ίσος του είκοσι (20).
- Γ. Θα εμφανίζει σε ποια θέση βρίσκεται και ποιος είναι ο μικρότερος μέσος όρος. Θεωρήστε ότι είναι μοναδικός.
- Δ. Θα εμφανίζει το μέσο όρο όλων των μαθητών.
- Ε. Θα εμφανίζει με κατάλληλα μηνύματα το ποσοστό των μαθητών με μέσο όρο μεγαλύτερο του 18.
Ενοποιείστε τους αλγορίθμους των παραδειγμάτων 2.23, 2.24 και 2.25 σε έναν ενιαίο αλγόριθμο, στον οποίο να προτάξετε ένα μενού επιλογής μιας λειτουργίας. (βλ. παρ. 2.17).
Στο πλαίσιο των εικονικών μαθητικών επιχειρήσεων, να αναπτύξετε αλγόριθμο ο οποίος:
- Α. Θα διαβάζει και θα αποθηκεύει σε πίνακα τις εισπράξεις μιας επιχείρησης για κάθε μήνα ενός σχολικού έτους.
- Β. θα ταξινομεί τον πίνακα των εισπράξεων σε φθίνουσα σειρά και θα εμφανίζει τον ταξινομημένο πίνακα.
- Γ. θα εμφανίζει τη μικρότερη και τη μεγαλύτερη είσπραξη της επιχείρησης.
Τροποποιείστε τον αλγόριθμο του παραδείγματος 2.28, ώστε να βρίσκει το μέσο όρο κάθε μαθήματος (υποδ. Απαιτείται ο υπολογισμός αθροισμάτων κατά στήλη).
Ο επόμενος αλγόριθμος εκτελεί σειριακή αναζήτηση του στοιχείου Κ στον πίνακα Α. Εντοπίστε τις διαφορές με τον αλγόριθμο του παραδείγματος 2.29. Ποιος είναι προτιμότερος και γιατί; Να λάβετε υπόψη την περίπτωση επιτυχημένης και αποτυχημένης αναζήτησης.

Αλγόριθμος Αναζήτηση2

Δεδομένα // Α, Ν, Κ //

Βρέθηκε ← Ψευδής

Θέση ← 0

Για i από 1 μέχρι Ν

     Αν Κ = Α[i] τότε

         Θέση ← i

         Βρέθηκε ← Αληθής

     Tέλος_αν

Τέλος_επανάληψης

Αποτελέσματα // Βρέθηκε, Θέση //

Τέλος Αναζήτηση2
Στον αλγόριθμο του παραδείγματος 2.29 είναι γνωστό από την εκφώνηση, ότι δεν μπορεί

2η

ΕΝΟΤΗΤΑ

να υπάρχει στον πίνακα δεύτερη φορά το ίδιο σχολείο. Αν σε έναν πίνακα δεν είναι γνωστό αν υπάρχουν ή όχι επαναλήψεις των ίδιων στοιχείων, πώς πρέπει να αντιμετωπιστεί το πρόβλημα της αναζήτησης; Δώστε ένα σχετικό αλγόριθμο.
Αν ο πίνακας Α του παραδείγματος 2.29 ήταν ταξινομημένος, μήπως αυτή η επί πλέον γνώση μπορεί να επιφέρει κάποια βελτίωση στον αλγόριθμο σειριακής αναζήτησης; Αν ναι, εκπονήστε τον τροποποιημένο αλγόριθμο.
Να αναπτύξετε αλγόριθμο ο οποίος θα διαβάζει τις δικαιολογημένες και τις αδικαιολόγητες απουσίες ενός μαθητή καθώς και τον μέσο όρο του στα προφορικά και θα καλεί αλγόριθμο ο οποίος θα δέχεται τα παραπάνω στοιχεία και θα επιστρέφει το μήνυμα:
• «Έχει δικαίωμα εξέτασης τον Ιούνιο», αν ο μαθητής έχει μέχρι 64 απουσίες ή έχει μέχρι 114 απουσίες από τις οποίες οι αδικαιολόγητες δεν ξεπερνούν τις 64 ή έχει μέχρι 164 απουσίες από τις οποίες οι αδικαιολόγητες δεν ξεπερνούν τις 64 και ο μέσος όρος του στα προφορικά είναι πάνω από 15.
• «Έχει δικαίωμα εξέτασης τον Σεπτέμβριο», αν ο μαθητής έχει πάνω από 64 και μέχρι 114 απουσίες και οι αδικαιολόγητες ξεπερνούν τις 64 ή έχει πάνω από 114 και μέχρι 164 απουσίες από τις οποίες οι αδικαιολόγητες δεν ξεπερνούν τις 64 αλλά ο μέσος όρος του στα προφορικά δεν είναι πάνω από 15.
• «Επανάληψη χρονιάς», σε κάθε άλλη περίπτωση.
Ο καλών αλγόριθμος θα εκτυπώνει το μήνυμα.
Να αναπτύξετε αλγόριθμο ο οποίος θα διαβάζει έναν ακέραιο θετικό αριθμό, και θα καλεί αλγόριθμο ο οποίος θα υπολογίζει το πλήθος των ψηφίων του αριθμού. Ο καλούμενος αλγόριθμος, θα επιστρέφει το πλήθος των ψηφίων του αριθμού. Ο καλών αλγόριθμος θα εκτυπώνει το πλήθος.
Να αναπτύξετε αλγόριθμο ο οποίος:
- Α. Θα διαβάζει και θα καταχωρίζει σε έναν πίνακα 1000 στοιχείων ονόματα.
- Β. Θα διαβάζει ένα ζητούμενο όνομα.
- Γ. Θα καλεί αλγόριθμο, ο οποίος θα αναζητά στον πίνακα το όνομα που διαβάστηκε στο προηγούμενο ερώτημα και θα επιστρέφει το πλήθος των ατόμων που υπάρχουν με το όνομα αυτό. Ο καλών αλγόριθμος θα εκτυπώνει το πλήθος.
Να εκτελέσετε το παρακάτω τμήμα αλγορίθμου

x ← 20

Σ ← 0

Για α από 1 μέχρι 10 με_βήμα 3

     x ← x - α

     Σ ← Σ + x

     Αν Σ mod 2 = 0 τότε

         x ← x + 1

     Τέλος_αν

Τέλος_επανάληψης

Αποτελέσματα // x //
Το ακόλουθο τμήμα αλγορίθμου αναπτύχθηκε για να υπολογίζει το άθροισμα 5 αριθμών. Ωστόσο περιέχει λογικά λάθη. Να εντοπίσετε τα λογικά λάθη και να τον διορθώσετε.

Διάβασε x

Σ ← 0

Για i από 0 μέχρι 5

Διάβασε x

Σ ← Σ + x

Τέλος_επανάληψης

Εμφάνισε Σ + x
Το ακόλουθο τμήμα αλγορίθμου αναπτύχθηκε για να ελέγχει αν ένας αριθμός είναι θετικός. Ωστόσο περιέχει λογικό λάθος. Να το εντοπίσετε.

Επανάλαβε

Διάβασε α

Μέχρις_ότου α < 0