ΚΕΦΑΛΑΙΟ13

ΣΤΕΡΕΑ ΣΧΗΜΑΤΑ

Στο κεφάλαιο αυτό θα μελετήσουμε δύο οικογένειες στερεών σχημάτων, τα πολύεδρα και τα στερεά εκ περιστροφής. Τα πολύεδρα αποτελούνται από τμήματα επιπέδων, κατάλληλα τοποθετημένα, ώστε να σχηματίζουν ένα κλειστό στερεό σύνολο. Υπάρχουν πολλά είδη πολυέδρων, εδώ όμως θα μελετήσουμε τα απλούστερα από αυτά, όπως είναι τα πρίσματα και οι πυραμίδες. Τα στερεά εκ περιστροφής με τα οποία θα ασχοληθούμε είναι ο κύλινδρος, ο κώνος και η σφαίρα. Τα στερεά αυτά λέγονται έτσι γιατί σχηματίζονται κατά την περιστροφή επίπεδων σχημάτων, όπως είναι το ορθογώνιο παραλληλόγραμμο, το ορθογώνιο τρίγωνο και ο κύκλος.
Τα πολύεδρα αποτελούν μία κατηγορία σχημάτων του χώρου, τα οποία παρουσιάζουν θεωρητικό ενδιαφέρον, είναι όμως χρήσιμα και από πλευράς εφαρμογής σε διάφορους τομείς της τεχνολογίας και της τέχνης. Στις διάφορες εφαρμογές χρησιμοποιούνται για να προσομοιάζουν σχήματα του φυσικού χώρου που συναντάμε γύρω μας και είναι σημαντικές όχι μόνο οι μετρικές αλλά και οι καθαρά γεωμετρικές ιδιότητές τους.

Πυραμίδα

Πυραμίδα, είσοδος στο μουσείο του Λούβρου, Παρίσι (1989).
Αρχιτέκτων ο Γιέο Μιγκ Πει.

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

13.1 Περί πολυέδρων

Στο κεφάλαιο 12 μελετήσαμε τις δίεδρες γωνίες, τα σχήματα δηλαδή που αποτελούνται από δύο τεμνόμενα επίπεδα. Στο κεφάλαιο αυτό θα χρειασθούμε την έννοια της τρίεδρης ή πολυεδρικής γωνίας, τα σχήματα δηλαδή που σχηματίζονται ή αποτελούνται από τρία ή περισσότερα επίπεδα. Δίνουμε λοιπόν τους ακόλουθους ορισμούς.

Ορισμός
Τρίεδρη γωνία λέγεται το σχήμα που καθορίζεται από τρεις ημιευθείες Ox, Oy και Οζ, με κοινή αρχή Ο, που δεν είναι συνεπίπεδες.

Μικροπείραμα

Το σημείο Ο λέγεται κορυφή της τρίεδρης, οι ημιευθείες Ox, Oy και Oz λέγονται ακμές της τρίεδρης. Αν Α, Β και Γ είναι τρία σημεία στις ακμές της τρίεδρης, οι γωνίες ΑÔΒ, ΒÔΓ και ΓÔΑ λέγονται έδρες ή επίπεδες γωνίες της τρίεδρης και τέλος οι δίεδρες γωνίες της τρίεδρης είναι ΟΑ(Β,Γ), ΟΒ(Α,Γ) και ΟΓ(Α,Β) με ακμές τις ΟΑ, ΟΒ και ΟΓ και έδρες τα τρία επίπεδα που ορίζουν οι ακμές ανά δύο. Η τρίεδρη γωνία συμβολίζεται με Ο.ΑΒΓ ή Ο.ξζε, όπου ε, ζ και ξ είναι οι ακμές της τρίεδρης (σχ.1).

Μία τυχαία ημιευθεία ΟΧ λέγεται εσωτερική της τρίεδρης Ο.ΑΒΓ αν η ΟΧ τέμνει το τρίγωνο ΑΒΓ σε εσωτερικό σημείο Χ. Ένα σημείο Χ του χώρου χαρακτηρίζεται ως εσωτερικό αν ανήκει σε μία εσωτερική ημιευθεία ΟΧ.

Αντίστοιχος ορισμός δίνεται και για την πολυεδρική γωνία.

Ορισμός II
Πολυεδρική γωνία λέγεται το σχήμα που αποτελείται από ν διατεταγμένες ημιευθείες ΟΑ1, ΟΑ2, ..., ΟΑν, με κοινή αρχή το σημείο Ο, που ανά τρεις διαδοχικές δεν είναι συνεπίπεδες (σχ.2).

Το σημείο Ο λέγεται κορυφή της πολυεδρικής, οι ημιευθείες λέγονται ακμές, ανά δύο διαδοχικές ακμές ορίζουν μία έδρα ή επίπεδη γωνία και ανά δύο διαδοχικές έδρες ορίζουν μία δίεδρη γωνία της πολυεδρικής στερεάς γωνίας.

Μία πολυεδρική γωνία με τέσσερις, πέντε κτλ. ακμές λέγεται αντίστοιχα τετράεδρη, πεντάεδρη κτλ. γωνία.

Σχήμα 1

Σχήμα 1

Σχήμα 2

Σχήμα 2

Κ Ε Φ Α Λ Α Ι Ο 13. Σ Τ Ε Ρ Ε Α Σ Χ Η Μ Α Τ Α

Σχήμα 3

Σχήμα 4

Σχήμα 4

Μία πολυεδρική γωνία λέγεται κυρτή, αν το επίπεδο της κάθε έδρας αφήνει την πολυεδρική γωνία στο ίδιο μέρος του χώρου.

Ορισμός II
Απλό πολύεδρο ή ?πολύεδρο ή ν-εδρο λέγεται το πεπερασμένο σχήμα του χώρου, το οποίο περικλείεται από ν επίπεδα πολυγωνικά σχήματα, που λέγονται έδρες του πολυέδρου.

Μικροπείραμα

Οι έδρες του πολυέδρου αποτελούν την επιφάνεια του πολυέδρου. Η κάθε πλευρά των εδρών ανήκει σε δύο ακριβώς έδρες και λέγεται ακμή του πολυέδρου. Η κάθε κορυφή των εδρών ανήκει σε τρεις ή περισσότερες έδρες του πολυέδρου και λέγεται κορυφή του πολυέδρου. Ένα πολύεδρο λέγεται κυρτό, αν το επίπεδο της κάθε έδρας αφήνει ολόκληρο το πολύεδρο στον έναν ημιχώρο. Αντίθετα, αν υπάρχουν κορυφές του πολυέδρου που βρίσκονται εκατέρωθεν του επιπέδου μίας τουλάχιστον έδρας, τότε το πολύεδρο λέγεται μη κυρτό. Στο βιβλίο αυτό θα ασχοληθούμε μόνο με κυρτά πολύεδρα. Στο σχ.3 παριστάνονται μερικά κυρτά πολύεδρα. Στο σχ.4, το σημείο Α είναι μία κορυφή, το τμήμα ΑΔ είναι μία ακμή και το τετράγωνο ΑΔΔ'Α' είναι μία έδρα του εικονιζόμενου πολύεδρου που λέγεται κύβος.

Ανά δύο οι κορυφές του πολυέδρου που δεν ανήκουν στην ίδια έδρα ορίζουν ευθύγραμμα τμήματα που λέγονται διαγώνιοι του πολυέδρου. Επίσης, ανά τρεις οι κορυφές του πολυέδρου που δεν ανήκουν στην ίδια έδρα ορίζουν επίπεδα που λέγονται διαγώνια επίπεδα του πολυέδρου. Στο σχ.4 το επίπεδο ΑΔΓ'Β' είναι ένα διαγώνιο επίπεδο και το τμήμα ΑΓ' μία διαγώνιος του κύβου.

Ενδεικτικά αναφέρουμε μερικές προτάσεις που ισχύουν στα πολύεδρα:

Οι έδρες ενός κυρτού πολύεδρου και οι επίπεδες τομές του είναι κυρτά πολύγωνα.
Κάθε ευθεία τέμνει ένα κυρτό πολύεδρο το πολύ σε δύο σημεία.
Αν Κ είναι το πλήθος των κορυφών, Α το πλήθος των ακμών και Ε το πλήθος των εδρών απλού πολυέδρου, ισχύει η σχέση Κ-Α+Ε=2 (Θεώρημα του Euler).

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

Πρίσματα

13.2 Ορισμός και στοιχεία του πρίσματος

• Πρισματική επιφάνεια

Θεωρούμε σε ένα επίπεδο π μία κλειστή πολυγωνική γραμμή με ν κορυφές και μία ευθεία ε, που τέμνει το π. Το σύνολο των ευθειών που είναι παράλληλες στην ε και διέρχονται από τα σημεία της πολυγωνικής γραμμής λέγονται γενέτειρες (σχ.5) και συνιστούν μία επιφάνεια που λέγεται πρισματική επιφάνεια. Η πολυγωνική γραμμή λέγεται οδηγός γραμμή. Οι γενέτειρες που διέρχονται από τις κορυφές της πολυγωνικής γραμμής λέγονται ακμές της πρισματικής επιφάνειας. Το σύνολο των γενετειρών, που τέμνουν μία πλευρά της πολυγωνικής γραμμής, σχηματίζει μία επίπεδη επιφάνεια που λέγεται έδρα της πρισματικής επιφάνειας. Η πρισματική επιφάνεια λέγεται κυρτή ή μη κυρτή, αν η οδηγός γραμμή είναι κυρτή ή όχι. Στα επόμενα θα ασχοληθούμε με κυρτές πρισματικές επιφάνειες. Κάθε επίπεδο που τέμνει μία ακμή θα τέμνει όλες τις ακμές και η πολυγωνική γραμμή που σχηματίζεται λέγεται επίπεδη τομή της πρισματικής επιφάνειας. Παράλληλα επίπεδα τέμνουν την πρισματική επιφάνεια σε ίσες πολυγωνικές γραμμές. Αν το επίπεδο τέμνει κάθετα τις ακμές, τότε η τομή λέγεται κάθετη τομή.

• Πρίσμα

Το στερεό σχήμα που περικλείεται μεταξύ δύο παραλλήλων επιπέδων και μιας πρισματικής επιφάνειας (σχ.6), συμπεριλαμβανομένων των επίπεδων τομών, λέγεται πρίσμα. Οι δύο ίσες και παράλληλες τομές λέγονται βάσεις του πρίσματος. Κάθε ευθύγραμμο τμήμα που έχει άκρα στα επίπεδα των βάσεων και είναι κάθετο σε αυτά λέγεται ύψος του πρίσματος. Τα τμήματα των εδρών της πρισματικής επιφάνειας που περικλείονται μεταξύ των επιπέδων των βάσεων είναι παραλληλόγραμμα και λέγονται παράπλευρες έδρες του πρίσματος. Τα τμήματα των ακμών της πρισματικής επιφάνειας που περιλαμβάνονται μεταξύ των επιπέδων των βάσεων λέγονται παράπλευρες ακμές του πρίσματος. Οι κορυφές των βάσεων λέγονται κορυφές του πρίσματος. Οι πλευρές των βάσεων λέγονται ακμές του πρίσματος. Αν οι βάσεις είναι κάθετες τομές, το πρίσμα λέγεται ορθό. Το πρίσμα λέγεται τριγωνικό, τετραγωνικό, ν-γωνικό, αν οι βάσεις του είναι τρίγωνα, τετράπλευρα, ν-γωνα. Το πρίσμα λέγεται κανονικό, αν είναι ορθό και οι βάσεις είναι κανονικά πολύγωνα. Ένα πρίσμα

Σχήμα 5

Σχήμα 6

Κ Ε Φ Α Λ Α Ι Ο 13. Σ Τ Ε Ρ Ε Α Σ Χ Η Μ Α Τ Α

Σχήμα 7

Σχήμα 7

Σχήμα 8

Σχήμα 8

Σχήμα 9

Σχήμα 9

Σχήμα 10

Σχήμα 10

σημειώνεται γράφοντας τις κορυφές του πολυγώνου της μίας βάσης το σύμβολο - και στη συνέχεια τις κορυφές της άλλης βάσης με την ίδια φορά. Έτσι, το πενταγωνικό πρίσμα που εικονίζεται στο σχ. 6 γράφεται ΑΒΓΔΕ-Α'Β'Γ'Δ'Ε'.

Αν οι βάσεις ενός πρίσματος είναι παραλληλόγραμμα, τότε το πρίσμα λέγεται παραλληλεπίπεδο (σχ.7). Αν το πρίσμα είναι ορθό και οι βάσεις είναι ορθογώνια, το πρίσμα λέγεται ορθογώνιο παραλληλεπίπεδο (σχ.8). Ειδικότερα, αν το ορθογώνιο παραλληλεπίπεδο έχει όλες τις ακμές ίσες, λέγεται κύβος (σχ.9).

Από τα παραπάνω προκύπτει ότι σε κάθε πρίσμα ισχύουν οι προτάσεις:

οι παράπλευρες έδρες είναι παραλληλόγραμμα,
οι παράπλευρες ακμές είναι ίσες,
οι βάσεις είναι ίσες.

13.3 Παραλληλεπίπεδο - κύβος.

ΘΕΩΡΗΜΑ Ι

Οι απέναντι έδρες ενός παραλληλεπιπέδου είναι ίσες και παράλληλες.

ΑΠΟΔΕΙΞΗ

Έστω το παραλληλεπίπεδο ΑΒΓΔ-Α'Β'Γ'Δ' (σχ. 10). Οι απέναντι έδρες ΑΒΒ'Α' και ΔΓΓ'Δ' έχουν:

ΑΒ=//ΔΓ από το παραλληλόγραμμο ΑΒΓΔ, ΑΑ'=//ΔΔ' από την έδρα ΑΑ'Δ'Δ και ΒAΑ' = ΓΔΔ' γιατί έχουν πλευρές παράλληλες μία προς μία και ομόρροπες. Άρα, τα παραλληλόγραμμα είναι ίσα και τα επίπεδά τους παράλληλα.

Από το θεώρημα αυτό προκύπτει ότι μπορούμε σε ένα παραλληλεπίπεδο να θεωρήσουμε οποιοδήποτε ζεύγος απέναντι εδρών ως βάσεις. Κάθε ακμή ενός παραλληλεπιπέδου είναι ίση με τις παράλληλές της, επομένως οι ακμές του παραλληλεπιπέδου χωρίζονται σε τρεις τετράδες ίσων ακμών.

ΠΟΡΙΣΜΑ Ι

Οι παράπλευρες έδρες ορθού πρίσματος είναι ορθογώνια.

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

Ορισμός
Διαστάσεις ενός ορθογώνιου παραλληλεπιπέδου λέγονται τα μήκη των τριών ακμών που έχουν κοινό το ένα άκρο τους.

ΘΕΩΡΗΜΑ IΙ

Σε κάθε ορθογώνιο παραλληλεπίπεδο το τετράγωνο της διαγωνίου δ ισούται με το άθροισμα των τετραγώνων των τριών διαστάσεων του ορθογώνιου παραλληλεπιπέδου, δηλαδή
δ²=α²+β²+γ².

ΑΠΟΔΕΙΞΗ

Από το ορθογώνιο τρίγωνο ΑΔΓ (σχ. 11), προκύπτει ότι

ΑΓ²=ΑΔ²+ΔΓ² ⇔ ΑΓ²=α²+β² (1).

Από το επίσης ορθογώνιο τρίγωνο ΑΓΓ' έχουμε

ΑΓ'²=ΑΓ²+ΓΓ'² ⇔ δ²=ΑΓ²+γ² (2)

Αντικαθιστώντας στη (2) το ΑΓ² από την (1), έχουμε το ζητούμενο: δ²=α²+β²+γ².

ΠΟΡΙΣΜΑ ΙI

Η διαγώνιος δ κύβου ακμής α είναι $δ = α\sqrt{3}$.

13.4 Μέτρηση πρίσματος

• Εμβαδόν επιφάνειας ορθού πρίσματος

Η επιφάνεια ενός ορθού ν-γωνικού πρίσματος (σχ.12) αποτελείται από ν παράπλευρες έδρες και δύο βάσεις. Το εμβαδόν της παράπλευρης επιφάνειας ορθού πρίσματος Ε_π είναι το άθροισμα των εμβαδών των παράπλευρων εδρών του πρίσματος ενώ το εμβαδόν της ολικής επιφάνειας του πρίσματος Ε_ο είναι το άθροισμα του εμβαδού της παράπλευρης επιφάνειας και του εμβαδού των δύο βάσεων. Αν υ είναι το ύψος του ορθού πρίσματος και α₁,α₂, ... α_ν είναι τα μήκη των πλευρών των βάσεων, τότε έχουμε την ακόλουθη πρόταση.

Σχήμα 11

Σχήμα 12

Κ Ε Φ Α Λ Α Ι Ο 13. Σ Τ Ε Ρ Ε Α Σ Χ Η Μ Α Τ Α

Σχήμα 13

ΠΡΟΤΑΣΗ

Το εμβαδόν της παράπλευρης επιφάνειας Ε_π και της ολικής επιφάνειας Ε_ο ενός ορθού πρίσματος με ύψος υ και μήκη πλευρών των βάσεων α₁, α₂,......, α_ν, δίνεται από τις σχέσεις:

Ε_π = s • υ και Ε_ο=E_π +2Β,

όπου s είναι η περίμετρος και Β το εμβαδόν της μίας βάσης του.

ΑΠΟΔΕΙΞΗ

Καθεμία από τις παράπλευρες έδρες είναι ορθογώνιο παραλληλόγραμμο, που η μία του πλευρά είναι ίση με το ύψος υ του ορθού πρίσματος, ενώ η άλλη πλευρά είναι μία από τις πλευρές των ίσων βάσεων. Το εμβαδόν λοιπόν της παράπλευρης επιφάνειας του ορθού πρίσματος Ε_π δίνεται από τη σχέση:

Ε_π = α₁•υ+α₂•υ+...+α_ν•υ=(α₁+α₂+...+α_ν)•υ= s•υ,

όπου s είναι η περίμετρος της βάσης.

Αν Β είναι το εμβαδόν της βάσης του ορθού πρίσματος, το εμβαδόν της ολικής επιφάνειας προφανώς δίνεται από τη σχέση

Ε_ο =Ε_π +2Β.

• Ανάπτυγμα ορθού πρίσματος

Θεωρούμε το ορθό τετραγωνικό πρίσμα ΑΒΓΔ-Α'Β'Γ'Δ' (σχ.13). Η παράπλευρη επιφάνεια του πρίσματος αποτελείται από ορθογώνια παραλληλόγραμμα, τα οποία όμως ανήκουν σε διαφορετικά επίπεδα. Κατασκευάζουμε το ανάπτυγμα της παράπλευρης επιφάνειας του πρίσματος ως εξής: Στο επίπεδο μίας έδρας κατακλίνουμε όλες τις έδρες του πρίσματος με τη σειρά που αυτές είναι τοποθετημένες στο χώρο, σαν να ξετυλίγουμε τις παράπλευρες έδρες του πρίσματος και τις δύο βάσεις του πάνω στο επίπεδο μίας έδρας. Το σχήμα που προκύπτει από την ανάπτυξη της παράπλευρης επιφάνειας του πρίσματος αποτελείται από ορθογώνια παραλληλόγραμμα ίσα με τις αντίστοιχες έδρες του πρίσματος, τοποθετημένα το ένα δίπλα στο άλλο, με τη σειρά που οι αντίστοιχες έδρες είναι τοποθετημένες στο χώρο. Λόγω της ισότητας αυτής, από το ανάπτυγμα του πρίσματος μπορούμε να υπολογίσουμε το εμβαδόν της παράπλευρης και ολικής επιφάνειας του πρίσματος και γενικά να λύσουμε προβλήματα που έχουν σχέση με την επιφάνεια του πρίσματος.

Από το ανάπτυγμα του πρίσματος μπορούμε να κατασκευάσουμε πρακτικά το πρίσμα. Αν, δηλαδή, κόψουμε το σχήμα

Μικροπείραμα

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

Α₀Β₀Γ₀Δ₀Α₀Α'₀Δ'₀Γ'₀Β'₀Α'₀ με ένα ψαλίδι και τσακίσουμε το χαρτί κατά μήκος των ευθύγραμμων τμημάτων Β₀Β'₀, Γ₀Γ'₀ και Δ₀Δ'₀, ώστε να ταυτιστούν τα δύο ευθύγραμμα τμήματα με άκρα τα σημεία Α₀ και Α'₀, έχουμε ένα πρίσμα με αυτό το ανάπτυγμα. Για να κατασκευάσουμε το συγκεκριμένο πρίσμα χρειαζόμαστε και τις δύο βάσεις του, ώστε να προσδιοριστούν οι δίεδρες γωνίες του πρίσματος.

Από το ανάπτυγμα του πρίσματος είναι φανερό ότι το εμβαδόν της παράπλευρης επιφάνειας ορθού πρίσματος ισούται με το εμβαδόν ορθογώνιου παραλληλογράμμου που η μία του πλευρά είναι το ύψος υ του πρίσματος και η άλλη του πλευρά είναι η περίμετρος μίας βάσης του.

• Όγκος πρίσματος

Ορισμός
Όγκος ενός πολυέδρου Π με μονάδα μέτρησης το πολύεδρο Π' λέγεται ο αριθμός που δηλώνει ότι το πολύεδρο Π γίνεται με επαναλήψεις του Π' ή των μερών του.

Ο όγκος δηλαδή είναι ο λόγος δύο πολυέδρων και είναι θετικός αριθμός. Ως μονάδα μέτρησης των όγκων λαμβάνεται ο κύβος με ακμή μήκους μία μονάδα. Δύο πολύεδρα λέγονται ισοδύναμα αν έχουν ίσους όγκους. Τον όγκο ενός πολυέδρου Π τον συμβολίζουμε με (Π).

Ιδιότητες του όγκου:

Δύο ίσα πολύεδρα έχουν ίσους όγκους.
Το μέρος ενός πολυέδρου έχει όγκο μικρότερο του αρχικού πολυέδρου.
Αν ένα πολύεδρο χωρισθεί σε άλλα πολύεδρα, τα οποία δεν έχουν κοινά εσωτερικά σημεία, τότε ο όγκος του αρχικού πολυέδρου ισούται με το άθροισμα των όγκων των μερών του (σχ.14α). (Τα επίπεδα σχήματα έχουν μηδενικό όγκο).

Στο σχ.14β έχουμε ένα παράδειγμα μέτρησης του κύβου Κ με μονάδα τον κύβο Κ'. Επειδή ο κύβος Κ' δε χωράει ακέραιες φορές στον κύβο Κ, υποδιαιρούμε τον κύβο Κ' σε μικρότερους κύβους, εδώ σε 8, και ο κύβος Κ γίνεται με 27 επαναλήψεις του 18 του κύβου Κ', δηλαδή (Κ) = 278 (Κ'). Επομένως, με μονάδα τον κύβο Κ' ο κύβος Κ έχει όγκο:

Σχήμα 14

Κ Ε Φ Α Λ Α Ι Ο 13. Σ Τ Ε Ρ Ε Α Σ Χ Η Μ Α Τ Α

Σχήμα 15

Σχήμα 16

Αποδεικνύεται ότι ισχύουν τα ακόλουθα θεωρήματα:

ΘΕΩΡΗΜΑΤΑ

i) Ο όγκος V ορθογώνιου παραλληλεπιπέδου ισούται με το γινόμενο των τριών διαστάσεών του, δηλαδή V=αβγ (σχ. 15α).

ii) Ο όγκος V κάθε παραλληλεπιπέδου ισούται με το γινόμενο του εμβαδού της βάσης Β επί το αντίστοιχο ύψος υ, δηλαδή V=B • υ (σχ. 15β).

ΠΟΡΙΣΜΑΤΑ I

• Ο όγκος κύβου ακμής μήκους α ισούται με α$^3$.
• Ο όγκος ενός ορθογώνιου παραλληλεπιπέδου ισούται με το εμβαδόν την βάσης του επί το αντίστοιχο ύψος.

Αν τμήσουμε ένα πλάγιο πρίσμα (σχ.16α) σε δύο μέρη με ένα επίπεδο κάθετο στις ακμές του, που το τέμνει μεταξύ των βάσεων, και μετακινήσουμε τα δύο μέρη έτσι ώστε να έρθουν σε επαφή οι δύο βάσεις του πρίσματος, ταυτίζοντας τις αντίστοιχες κορυφές, τότε δημιουργείται ένα ορθό πρίσμα (σχ.16β) που έχει βάσεις ίσες με την κάθετη τομή και ύψος ίσο με την ακμή του πρίσματος. Ισχύει δηλαδή το επόμενο θεώρημα:

ΘΕΩΡΗΜΑ Ι

Κάθε πλάγιο πρίσμα είναι ισοδύναμο με ορθό πρίσμα που έχει ως βάση μία κάθετη τομή του πλάγιου πρίσματος και ως ύψος την ακμή του.

Όπως είδαμε παραπάνω, ο όγκος ενός παραλληπεπιπέδου ισούται με το γινόμενο του εμβαδού της βάσης επί το αντίστοιχο ύψος του. Τώρα θα αποδείξουμε ότι αυτό ισχύει σε κάθε πρίσμα.

ΘΕΩΡΗΜΑ ΙΙ

Κάθε διαγώνιο επίπεδο ενός παραλληλεπιπέδου το χωρίζει σε δύο ισοδύναμα τριγωνικά πρίσματα.

ΑΠΟΔΕΙΞΗ

Αν το παραλληλεπίπεδο είναι ορθό, χωρίζεται από ένα διαγώνιο

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

επίπεδο σε δύο ίσα ορθά πρίσματα, που έχουν ίσες βάσεις και ίσα ύψη, επομένως είναι ισοδύναμα.

Έστω ΑΒΓΔ-Α'Β'Γ'Δ' τυχαίο παραλληλεπίπεδο και Γ'ΓΑΑ' ένα διαγώνιο επίπεδο (σχ.17), που το χωρίζει σε δύο τριγωνικά πρίσματα. Αν ΚΛΜΝ είναι μία τομή κάθετη στην ακμή ΑΑ', τότε, σύμφωνα με το θεώρημα I οι όγκοι των δύο πρισμάτων ΑΒΓ-Α'Β'Γ' είναι (ΚΛΜ) • ΑΑ' και (ΚΜΝ) • ΔΔ' αντίστοιχα. Αλλά ΑΑ' = ΔΔ' και (ΚΛΜ) = (ΚΜΝ), διότι το ΚΛΜΝ είναι παραλληλόγραμμο που χωρίζεται από τη διαγώνιό του και σε δύο ίσα τρίγωνα. Επομένως τα δύο πρίσματα είναι ισοδύναμα.

ΠΟΡΙΣΜΑΤΑ II

i) Ο όγκος τριγωνικού πρίσματος ισούται με το γινόμενο του εμβαδού της τριγωνικής βάσης επί το ύψος.
ii) Ο όγκος κάθε πρίσματος ισούται με το εμβαδόν της βάσης επί το ύψος.

ΑΠΟΔΕΙΞΗ

i) Έστω το τριγωνικό πρίσμα ΑΒΓ-Α'Β'Γ' (σχ.18). Σχηματίζουμε το παραλληλεπίπεδο ΑΒΓΔ-Α'Β'Γ'Δ', του οποίου ο όγκος ισούται με το γινόμενο του εμβαδού της βάσης επί το ύψος. Όμως, το διαγώνιο επίπεδο Γ'ΓΑΑ' χωρίζει το παραλληλεπίπεδο σε δύο ισοδύναμα τριγωνικά πρίσματα. Άρα, ο όγκος V του τριγωνικού πρίσματος δίνεται από τη σχέση:

V = 12 εμβ(ΑΒΓΔ) • υ = εμβ(ΑΒΓ) • υ = Β • υ ,

όπου Β το εμβαδόν του τριγώνου της βάσης ΑΒΓ και υ το ύψος του πρίσματος.

ii) Εφαρμόζουμε το Πόρισμα (i) σε κάθε ένα από τα (ν-2) τριγωνικά πρίσματα στα οποία χωρίζεται ένα ν-γωνικό πρίσμα από τα διαγώνια επίπεδα που διέρχονται από μία παράπλευρη ακμή του.

Σχήμα 17

Σχήμα 18

ΕΦΑΡΜΟΓΗ

Οι τέσσερις διαγώνιοι ενός παραλληλεπιπέδου διχοτομούνται.

Απόδειξη

Έστω το παραλληλεπίπεδο ΑΒΓΔ-Α'Β'Γ'Δ' και οι διαγώνιοι ΑΓ', Α'Γ, ΒΔ' και Β'Δ (σχ.19). Θα αποδείξουμε ότι δύο από αυτές, έστω οι ΑΓ' και Α'Γ διχοτομούνται. Το τετράπλευρο ΑΑ'Γ'Γ είναι παραλληλόγραμμο, διότι έχει δύο απέναντι πλευρές, τις ΑΑ' και ΓΓ', ίσες και παράλληλες, ως παράπλευρες ακμές του παραλληλεπιπέδου. Επομένως οι διαγώνιοί του διχοτομούνται. Όμοια αποδεικνύεται ότι η διαγώνιος ΑΓ' διχοτομείται με τις ΒΔ' και Β'Δ.

Σχήμα 19

Κ Ε Φ Α Λ Α Ι Ο 13. Σ Τ Ε Ρ Ε Α Σ Χ Η Μ Α Τ Α

ΑΣΚΗΣΕΙΣ ΓΙΑ ΛΥΣΗ

Ασκήσεις Εμπέδωσης

1. Να αποδείξετε ότι το ύψος πλάγιου πρίσματος είναι μικρότερο από την ακμή του.
2. Να αποδείξετε ότι οι κάθετες τομές ορθού πρίσματος είναι ίσες με τις βάσεις του και τα ύψη ίσα με τις ακμές του.
3. Να αποδείξετε ότι όλες οι ακμές πλάγιου πρίσματος σχηματίζουν ίσες γωνίες με τα επίπεδα των βάσεων.
4. Κανονικό τριγωνικό πρίσμα έχει ύψος α και βάση ισόπλευρο τρίγωνο πλευράς α. Να υπολογίσετε το εμβαδόν της ολικής επιφάνειας και τον όγκο του πρίσματος.
5. Να υπολογίσετε το εμβαδόν της ολικής επιφάνειας κανονικού πρίσματος ύψους υ με βάση κανονικό πολύγωνο εγγεγραμμένο σε κύκλο ακτίνας ρ, αν η βάση είναι τρίγωνο, τετράγωνο ή εξάγωνο.
6. Να αποδείξετε ότι κάθε ευθύγραμμο τμήμα που διέρχεται από το κέντρο παραλληλεπιπέδου και έχει τα άκρα του στην επιφάνειά του διχοτομείται από το κέντρο.
7. Για την κατασκευή μιας κυβικής δεξαμενής, κλειστής από παντού, χρησιμοποιήθηκαν 216 m² λαμαρίνας. Να υπολογίσετε την ακμή του κύβου.
8. Ορθογώνιο παραλληλεπίπεδο έχει διαστάσεις 8, 12, 16. Να υπολογίσετε την διαγώνιο, το εμβαδόν της επιφάνειας και τον όγκο του.
9. Να υπολογίσετε το εμβαδόν της ολικής επιφάνειας και τον όγκο ενός κύβου αν γνωρίζετε: (i) την ακμή του, (ii) τη διαγώνιο μιας έδρας του, (iii) τη διαγώνιό του.
10. Κύβος έχει όγκο 125. Να υπολογίσετε το εμβαδόν της ολικής επιφάνειάς του.

Αποδεικτικές Ασκήσεις

1. Να αποδείξετε ότι ο όγκος ενός τριγωνικού πρίσματος ισούται με το ημιγινόμενο μιας παράπλευρης έδρας επί την απόστασή της από την απέναντι ακμή.
2. Να αποδείξετε ότι ο όγκος ενός πρίσματος που η κάθετη τομή του είναι πολύγωνο περιγεγραμμένο σε έναν κύκλο, ισούται με το γινόμενο της παράπλευρης επιφάνειας επί το μισό της ακτίνας του κύκλου.

3. Δίνονται τρεις παράλληλες ευθείες που δεν ανήκουν στο ίδιο επίπεδο και τρία ίσα ευθύγραμμα τμήματα ΑΑ', ΒΒ' και ΓΓ' που ολισθαίνουν πάνω σε αυτές. Να αποδείξετε ότι το εμβαδόν της παράπλευρης επιφάνειας και ο όγκος του πρίσματος ΑΒΓ-Α'Β'Γ' είναι σταθερά.

Μικροπείραμα

4. Να αποδείξετε ότι το άθροισμα των τετραγώνων των προβολών ενός ευθύγραμμου τμήματος σε τρεις ευθείες, ανά δύο ορθογώνιες μεταξύ τους, ισούται με το τετράγωνο του τμήματος.
5. Να αποδείξετε ότι το άθροισμα των τετραγώνων των προβολών ενός ευθύγραμμου τμήματος σε τρία επίπεδα, ανά δύο κάθετα μεταξύ τους, ισούται με το διπλάσιο του τετραγώνου του τμήματος.

Μικροπείραμα

6. Σε έναν κύβο, να αποδείξετε ότι: (i) οι διαγώνιοι σχηματίζουν ίσες γωνίες με τις ακμές και (ii) η προβολή μιας ακμής σε μία διαγώνιο ισούται με το ένα τρίτο της διαγωνίου.

Μικροπείραμα

7. Δίνεται παραλληλεπίπεδο ΑΒΓΔ-Α'Β'Γ'Δ'. Να αποδείξετε ότι τα επίπεδα (Α, Γ, Δ') και (Α', Γ', Β) τριχοτομούν τη διαγώνιο ΔΒ'.

Μικροπείραμα

Σύνθετα Θέματα

1. Να αποδείξετε ότι η τομή κύβου με επίπεδο που ορίζεται από τα άκρα τριών ακμών που διέρχονται από την ίδια κορυφή είναι ισόπλευρο τρίγωνο.

Μικροπειράματα μικροπείραμα

2. Να αποδείξετε ότι τα τρία επίπεδα που ορίζονται από μία διαγώνιο κύβου και από τις τρεις ακμές που διέρχονται από το ένα άκρο της διαγωνίου σχηματίζουν ίσες δίεδρες.

Μικροπείραμα

3. Εάν τμηθεί κύβος ΑΒΓΔ-Α'Β'Γ'Δ' με επίπεδο που διέρχεται από τα μέσα των ακμών ΑΒ, ΒΓ και ΓΓ', να αποδείξετε ότι η τομή είναι κανονικό εξάγωνο.

Μικροπείραμα

4. Το άθροισμα των τετραγώνων των ακμών ενός παραλληλεπιπέδου ισούται με το άθροισμα των τετραγώνων των τεσσάρων διαγωνίων του.

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

ΔΡΑΣΤΗΡΙΟΤΗΤΑ

1. Σε ένα τετραγωνικό πρίσμα, να αποδείξετε ότι: (i) οι διαγώνιοι αποτελούν δύο ομάδες τεμνόμενων ευθειών, (ii) η απόσταση αυτών των κοινών σημείων ισούται με την απόσταση των μέσων των διαγωνίων της βάσης και (iii) να χρησιμοποιηθεί αυτή η ιδιότητα για να βρείτε ικανή και αναγκαία συνθήκη ώστε το πρίσμα να είναι παραλληλεπίπεδο.

2. Να αποδείξετε ότι σε ένα τριγωνικό πρίσμα:
i) απέναντι ίσων εδρών βρίσκονται ίσες δίεδρες,
ii) απέναντι της μεγαλύτερης έδρας βρίσκεται η μεγαλύτερη δίεδρη και
iii) το εμβαδόν κάθε έδρας είναι μικρότερο του αθροίσματος των δύο άλλων.

Μικροπείραμα

ΑΝΑΚΕΦΑΛΑΙΩΣΗ

1. Εμβαδόν

Το εμβαδόν παράπλευρης επιφάνειας ορθού πρίσματος ισούται με την περίμετρο της βάσης επί το μήκος της ακμής.
Το εμβαδόν της ολικής επιφάνειας πρίσματος ισούται με το εμβαδόν της παράπλευρης επιφάνειας αυξημένο κατά το εμβαδόν των δύο βάσεων.

2. Όγκος

Ο όγκος πρίσματος ισούται με το εμβαδόν της βάσης επί το ύψος του.
Ο όγκος πρίσματος ισούται με το εμβαδόν της κάθετης τομής επί το μήκος της ακμής του.
Ο όγκος ορθογωνίου παραλληλεπιπέδου ισούται με το γινόμενο των τριών διαστάσεών του.
Ο όγκος κύβου ισούται με τον κύβο της ακμής του.

3. Άλλες ιδιότητες

Οι απέναντι έδρες παραλληλεπιπέδου είναι ίσες και παράλληλες.
Οι διαγώνιοι παραλληλεπιπέδου διχοτομούνται.
Κάθε διαγώνιο επίπεδο παραλληλεπιπέδου το διαιρεί σε δύο ισοδύναμα τριγωνικά πρίσματα.
Αν α, β, γ οι διαστάσεις ορθογώνιου παραλληλεπιπέδου και δ η διαγώνιος, ισχύει

δ² = α² + β² + γ²

Πυραμίδες

13.5 Ορισμός και στοιχεία πυραμίδας

Θεωρούμε ένα επίπεδο κυρτό πολύγωνο Α₁Α₂....Α_νμε ν κορυφές και ένα σημείο Κ εκτός του επιπέδου του πολυγώνου. Το πολύεδρο, που έχει έδρες τα ν τρίγωνα ΚΑ₁Α₂, ΚΑ₂Α₃,..,

Κ Ε Φ Α Λ Α Ι Ο 13. Σ Τ Ε Ρ Ε Α Σ Χ Η Μ Α Τ Α

Σχήμα 20

Σχήμα 21

ΚΑ_νΑ₁ και το πολύγωνο Α₁Α₂....Α_ν, λέγεται ν-γωνική πυραμίδα και σημειώνεται Κ.Α₁Α₂ ... Α_ν. Το πολύγωνο λέγεται βάση της πυραμίδας, ενώ τα τρίγωνα με κοινή κορυφή το σημείο Κ και απέναντι πλευρές τις πλευρές της βάσης λέγονται παράπλευρες έδρες. Το κοινό σημείο Κ λέγεται κορυφή της πυραμίδας. Ανά δύο οι διαδοχικές παράπλευρες έδρες τέμνονται σε ευθύγραμμα τμήματα που λέγονται παράπλευρες ακμές της πυραμίδας. Το σύνολο των παράπλευρων εδρών λέγεται παράπλευρη επιφάνεια της πυραμίδας. Η πυραμίδα λέγεται τριγωνική, τετραγωνική, πενταγωνική κτλ., αν η βάση είναι τρίγωνο, τετράπλευρο, πεντάγωνο κτλ.

Στο σχ.20 παριστάνονται μία τριγωνική πυραμίδα, με κορυφή το σημείο Κ και βάση το τρίγωνο ΑΒΓ που σημειώνεται με Κ.ΑΒΓ, και μία πενταγωνική πυραμίδα, με κορυφή το σημείο Κ και βάση το πεντάγωνο ΑΒΓΔΕ που σημειώνεται με Κ.ΑΒΓΔΕ. To ευθύγραμμο τμήμα που άγεται από την κορυφή Κ της πυραμίδας κάθετα στο επίπεδο της βάσης λέγεται ύψος της πυραμίδας. Στο σχ.20 το τμήμα ΚΗ είναι το ύψος των πυραμίδων.

ΘΕΩΡΗΜΑ

Αν μία πυραμίδα τμηθεί με επίπεδο παράλληλο στη βάση της, τότε:

Οι παράπλευρες ακμές και το ύψος της πυραμίδας χωρίζονται σε μέρη ανάλογα.
Η τομή είναι πολύγωνο όμοιο της βάσης με λόγο ομοιότητας τον λόγο των αποστάσεων της κορυφής από τη βάση και την τομή.

ΑΠΟΔΕΙΞΗ

Αποδεικνύουμε το θεώρημα για μια τριγωνική πυραμίδα. Η απόδειξη για τυχούσα ν-γωνική πυραμίδα γίνεται με όμοιο τρόπο.

Έστω η πυραμίδα Κ.ΑΒΓ και ΚΗ το ύψος της (σχ.21). Φέρουμε ένα επίπεδο παράλληλο στη βάση, το οποίο τέμνει τις ακμές και το ύψος της πυραμίδας στα σημεία Α', Β', Γ' και Η' αντίστοιχα.

(i) Στην έδρα ΚΑΒ, οι πλευρές ΑΒ και Α'Β' είναι παράλληλες ως τομές των παράλληλων επιπέδων με την έδρα ΚΑΒ. Από τα όμοια τρίγωνα ΚΑΒ και ΚΑ'Β' προκύπτει η σχέση:

KAKA' = KBKB' = ABA'B' .

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

Εφαρμόζοντας τον ίδιο συλλογισμό για τις υπόλοιπες έδρες της πυραμίδας, προκύπτουν οι σχέσεις:

KAKA' = KBKB' = ΚΓΚΓ' = ΑΒA'B' = ΒΓB'Γ' = ΓΑΓ'A' = λ .

Επίσης, από τα όμοια τρίγωνα ΚΗΑ και ΚΗ'Α' προκύπτει:

KAKA' = KΗKΗ' = λ.

(ii) Η βάση και η τομή της πυραμίδας είναι δύο τρίγωνα (ν-γωνα) με τα ζεύγη των ομόλογων πλευρών τους παράλληλα και ομόρροπα, επομένως έχουν τις ομόλογες γωνίες ίσες. Επιπλέον, από τις παραπάνω σχέσεις τα ζεύγη των ομόλογων πλευρών είναι ανάλογα, άρα τα τρίγωνα είναι όμοια, με λόγο ομοιότητας λ.

13.6 Κανονική πυραμίδα-Τετράεδρο

Μία πυραμίδα λέγεται κανονική, αν η βάση είναι κανονικό πολύγωνο και η προβολή της κορυφής της πυραμίδας στο επίπεδο της βάσης είναι το κέντρο του κανονικού πολυγώνου (σχ.22). Σε μία κανονική πυραμίδα, οι παράπλευρες έδρες είναι ισοσκελή τρίγωνα, ίσα μεταξύ τους και το ύψος κάθε παράπλευρης έδρας που άγεται από την κορυφή της πυραμίδας λέγεται απόστημα ή παράπλευρο ύψος της κανονικής πυραμίδας (σχ.22). Αποδεικνύεται επίσης, ότι αν οι παράπλευρες έδρες μιας πυραμίδας είναι ίσα ισοσκελή τρίγωνα, τότε η πυραμίδα είναι κανονική.

Μία τριγωνική πυραμίδα (σχ.23α) λέγεται τετράεδρο, γιατί έχει τέσσερις τριγωνικές έδρες. Οποιαδήποτε έδρα του τετραέδρου μπορεί να θεωρηθεί ως βάση. Κανονικό λέγεται το τετράεδρο που όλες οι έδρες του είναι ίσα ισόπλευρα τρίγωνα (σχ.23β). Το τετράεδρο είναι το απλούστερο πολύεδρο.

13.7 Μέτρηση πυραμίδας

• Εμβαδόν κανονικής πυραμίδας

Το ανάπτυγμα της επιφάνειας κανονικής ν-γωνικής πυραμίδας στο επίπεδο της βάσης αποτελείται από το κανονικό πολύγωνο της βάσης και από τα ν ισοσκελή τρίγωνα των παράπλευρων εδρών τοποθετημένα αστεροειδώς στις πλευρές της βάσης (σχ.24). Από το ανάπτυγμα υπολογίζεται η παράπλευρη και η ολική επιφάνεια κανονικής ν-γωνικής πυραμίδας.

Σχήμα 22

Σχήμα 22

Σχήμα 23α

Σχήμα 23α

Σχήμα 23β

Σχήμα 23β

Κ Ε Φ Α Λ Α Ι Ο 13. Σ Τ Ε Ρ Ε Α Σ Χ Η Μ Α Τ Α

Σχήμα 24

Η παράπλευρη επιφάνεια Ε_π είναι το άθροισμα των εμβαδών των ν ισοσκελών τριγώνων που αποτελούν τις παράπλευρες έδρες της πυραμίδας, ενώ το εμβαδόν της ολικής επιφάνειας Ε_ο είναι το άθροισμα της παράπλευρης επιφάνειας και της βάσης. Το ανάπτυγμα πυραμίδας κατασκευάζεται επίσης, όταν χρειάζεται να κατασκευασθεί πρακτικά η πυραμίδα.

Μικροπείραμα

ΘΕΩΡΗΜΑ I

Το εμβαδόν της παράπλευρης Ε_π και της ολικής Ε_ο επιφάνειας κανονικής πυραμίδας δίνεται από τις σχέσεις

Ε_π = τ • μ και Ε_ο = τ • (μ + α),

όπου τ είναι η ημιπερίπετρος, α είναι το απόστημα της βάσης και μ το απόστημα της πυραμίδας.

ΑΠΟΔΕΙΞΗ

Η παράπλευρη επιφάνεια κανονικής πυραμίδας αποτελείται από ν ισοσκελή τρίγωνα, με βάση λ και απόστημα α, που έχουν εμβαδόν:

Για τον υπολογισμό του εμβαδού της συνολικής επιφάνειας της πυραμίδας, στην παράπλευρη επιφάνεια προσθέτουμε και το εμβαδόν της βάσης που είναι κανονικό ν-γωνο:

• Όγκος πυραμίδας
Δεχόμαστε χωρίς απόδειξη ότι:

ΘΕΩΡΗΜΑ ΙI

Δύο τριγωνικές πυραμίδες με ίσα ύψη και ίσες ή ισοδύναμες βάσεις είναι ίσες ή ισοδύναμες.

Το επόμενο θεώρημα είναι πολύ σημαντικό γιατί συσχετίζει τους όγκους ενός πρίσματος και μιας πυραμίδας που έχουν ίσες βάσεις και ίσα ύψη.

ΘΕΩΡΗΜΑ ΙΙI

Ο όγκος πυραμίδας ισούται με το ένα τρίτο του όγκου πρίσματος που έχει την ίδια βάση και το ίδιο ύψος.

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

ΑΠΟΔΕΙΞΗ

Έστω η τριγωνική πυραμίδα Κ.ΑΒΓ. Από τις κορυφές Β και Γ (σχ.25), φέρουμε τις παράλληλες και ίσες στην ΚΑ και σχηματίζεται το πρίσμα ΑΒΓ-ΚΒ'Γ'. Χωρίζουμε το πρίσμα στις εξής τρεις πυραμίδες: Κ.ΑΒΓ, Β.ΚΒ'Γ' και Κ.ΒΓΓ'. Οι δύο πρώτες πυραμίδες είναι ισοδύναμες, γιατί έχουν ως βάσεις τις ίσες βάσεις του πρίσματος και κοινό ύψος. Η δεύτερη και η τρίτη είναι επίσης ισοδύναμες, διότι αν θεωρήσουμε ότι έχουν κοινή κορυφή το σημείο Κ, οι βάσεις τους ΒΒ'Γ' και ΒΓΓ' είναι τα δύο ίσα τρίγωνα στα οποία χωρίζεται το παραλληλόγραμμο ΒΓΓ'Β' με τη διαγώνιό του ΒΓ'. Επίσης έχουν ίσα ύψη, αφού οι βάσεις τους είναι συνεπίπεδες. Παρατηρούμε δηλαδή ότι το πρίσμα χωρίστηκε σε τρεις ισοδύναμες πυραμίδες, άρα ο όγκος κάθε τριγωνικής πυραμίδας ισούται με το τρίτο του όγκου του πρίσματος που έχει την ίδια βάση και το ίδιο ύψος, δηλαδή συμβολικά V = E•υ3 , όπου V ο όγκος, Ε το εμβαδόν της βάσης και υ το ύψος της πυραμίδας.

Αν η πυραμίδα είναι ν-γωνική, την χωρίζουμε σε (ν-2) τριγωνικές πυραμίδες, φέροντας τις διαγωνίους της βάσης από μία κορυφή της. Για κάθε μία από τις τριγωνικές πυραμίδες αποδείξαμε ότι ισχύει το Θεώρημα, επομένως ο συνολικός όγκος της πυραμίδας ισούται με το άθροισμα των όγκων των τριγωνικών πυραμίδων, δηλαδή:

όπου Ε₁, Ε₂, ... είναι τα εμβαδά των (ν-2) τριγώνων που χωρίζεται η βάση, Ε το εμβαδόν της βάσης και υ το ύψος της πυραμίδας.

Μικροπείραμα

Σχήμα 25

ΕΦΑΡΜΟΓΗ 1η

Να υπολογισθεί το εμβαδόν της συνολικής επιφάνειας και ο όγκος κανονικού τετραέδρου, ακμής α.

Λύση

Η επιφάνεια του τετραέδρου αποτελείται από τέσσερα ισόπλευρα τρίγωνα πλευράς α, επομένως η συνολική επιφάνεια του τετραέδρου έχει εμβαδόν
$E = 4 \cdot α^2 \dfrac{\sqrt{3}}{4} = \sqrt{3} \cdot α^2$.
Ο όγκος του κανονικού τετραέδρου, θεωρούμενο ως τριγωνική πυραμίδα, ισούται με το τρίτο του εμβαδού της βάσης ΑΒΓ που είναι ισόπλευρο τρίγωνο πλευράς α, επί το ύψος ΔΚ. Το Κ όμως είναι κέντρο βάρους της βάσης και από το ορθογώνιο τρίγωνο ΑΔΚ έχουμε
$ΔΚ = \dfrac{α\sqrt{6}}{3}.$
Επομένως, ο όγκος του τετραέδρου είναι $V = \dfrac{1}{3} \cdot \dfrac{α^2\sqrt{3}}{4} \cdot \dfrac{α\sqrt{6}}{3} = \dfrac{α^3\sqrt{2}}{12}$.

Σχήμα 26

Κ Ε Φ Α Λ Α Ι Ο 13. Σ Τ Ε Ρ Ε Α Σ Χ Η Μ Α Τ Α

Σχήμα 27

13.8 Ορισμός και στοιχεία κόλουρης πυραμίδας

Αν τμήσουμε μία πυραμίδα μεταξύ κορυφής και βάσης, με επίπεδο παράλληλο στη βάση, τότε το μέρος της πυραμίδας που περιλαμβάνεται μεταξύ των δύο παράλληλων επιπέδων λέγεται κόλουρη πυραμίδα. Τα δύο όμοια πολύγωνα λέγονται βάσεις (μικρή και μεγάλη) της κόλουρης πυραμίδας και το ευθύγραμμο τμήμα που έχει άκρα στα επίπεδα των βάσεων και είναι κάθετο σε αυτά λέγεται ύψος της κόλουρης πυραμίδας.

Οι παράπλευρες έδρες μιας κόλουρης πυραμίδας είναι τραπέζια και τα ύψη τους λέγονται παράπλευρα ύψη της κόλουρης πυραμίδας. Ισοσκελής λέγεται η κόλουρη πυραμίδα που κατασκευάζεται από κανονική πυραμίδα και οι παράπλευρες έδρες της είναι ισοσκελή τραπέζια.

Στο σχ.27 παριστάνεται μια κόλουρη ισοσκελής τετραγωνική πυραμίδα, η οποία σημειώνεται με ΑΒΓΔ-Α'Β'Γ'Δ', έχει ύψος ΛΛ' και παράπλευρο ύψος ΗΗ'.

13.9 Μέτρηση κόλουρης ισοσκελούς πυραμίδας

• Εμβαδόν επιφάνειας κόλουρης ισοσκελούς πυραμίδας.
Το εμβαδόν Ε_π της παράπλευρης επιφάνειας κόλουρης ισοσκελούς πυραμίδας με βάσεις κανονικά ν-γωνα, ισούται με:

Ε_π = (τ+τ') • υ',

όπου τ και τ' είναι οι ημιπερίμετροι των βάσεων και υ' είναι το παράπλευρο ύψος της.
Το εμβαδόν της ολικής επιφάνειας δίνεται από τον τύπο:

Ε_ο = Ε_π + Β + β,

όπου Β και β είναι τα εμβαδά των δύο βάσεων.

• Όγκος κόλουρης ισοσκελούς πυραμίδας
Ο όγκος κόλουρης πυραμίδας δίνεται από τον τύπο:

$V = \dfrac{υ \cdot (Β + β + \sqrt{Ββ})}{3}$.

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

ΕΦΑΡΜΟΓΗ 1η

Να αποδειχθεί ότι τα μεσοκάθετα επίπεδα στις έξι ακμές ενός τετραέδρου διέρχονται από το ίδιο σημείο. Επίσης, οι ευθείες που είναι κάθετες στις έδρες τετραέδρου στα περίκεντρα των εδρών διέρχονται από το ίδιο σημείο.

Απόδειξη
Αν ΑΒΓΔ είναι ένα τετράεδρο, τα μεσοκάθετα επίπεδα στις ακμές ΑΒ, ΑΓ και ΑΔ τέμνονται σε σημείο Ο, διότι είναι κάθετα σε τρεις τεμνόμενες ευθείες.
Το σημείο Ο (σχ.28), ισαπέχει από τις κορυφές Α, Β, Γ και Δ άρα θα ανήκει και στα μεσοκάθετα επίπεδα των υπολοίπων ακμών.
Επίσης, το σημείο Ο ανήκει στα μεσοκάθετα επίπεδα των τριών ακμών κάθε έδρας, άρα προβάλλεται στα περίκεντρα των εδρών.

Μικροπείραμα

Σχήμα 28

ΕΦΑΡΜΟΓΗ 2η

Να βρεθεί σημείο που να ισαπέχει από τα επίπεδα των εδρών ενός τετραέδρου ΑΒΓΔ.

Απόδειξη
Τα σημεία της κοινής ευθείας ΑΧ (σχ.29), των επιπέδων που διχοτομούν τις δίεδρες ΑΒ(Γ,Δ), ΑΔ(Β,Γ) και ΑΓ(Β,Δ) ισαπέχουν από τις τρεις έδρες ΑΒΓ, ΑΒΔ και ΑΓΔ. Το επίπεδο που διχοτομεί τη δίεδρη ΒΔ(Α,Γ) τέμνει την ΑΧ σε ένα σημείο Ο, που ισαπέχει και από τις τέσσερις έδρες.

Μικροπείραμα

Σχήμα 29

ΑΣΚΗΣΕΙΣ ΓΙΑ ΛΥΣΗ

Ασκήσεις Εμπέδωσης

1. Να υπολογίσετε το ύψος και το απόστημα κανονικής (i) εξαγωνικής, (ii) τετραγωνικής και (iii) τριγωνικής πυραμίδας (κανονικό τετράεδρο), αν έχει πλευρά βάσης μήκους μ και ακμή μήκους λ.
2. Να αποδείξετε ότι οι παράπλευρες έδρες κανονικής ν-γωνικής πυραμίδας σχηματίζουν ίσες γωνίες με το επίπεδο της βάσης.
3. Να υπολογίσετε το εμβαδόν της παράπλευρης επιφάνειας και της ολικής επιφάνειας κανονικής τετραγωνικής πυραμίδας, με πλευρά βάσης 4 και ακμή 7.
4. Να υπολογίσετε το εμβαδόν της βάσης κανονικής τετραγωνικής πυραμίδας που έχει εμβαδόν παράπλευρης επιφάνειας 200 και απόστημα 10.
5. Η μεγάλη πυραμίδα της Αιγύπτου έχει βάση τετράγωνο πλευράς 234m και ύψος 146m. Να υπολογίσετε την παράπλευρη επιφάνεια και τον όγκο της πυραμίδας.

6. Να υπολογίσετε το εμβαδόν της παράπλευρης επιφάνειας και τον όγκο κανονικής τετραγωνικής πυραμίδας ως συνάρτηση της πλευράς της βάσης, αν έχει ακμή ίση με τη διαγώνιο της βάσης.
7. Να βρείτε το λόγο των όγκων κύβου και κανονικού τετραέδρου που έχει ακμή ίση με τη: (i) διαγώνιο του κύβου και (ii) διαγώνιο της έδρας του κύβου.
8. Να βρείτε το λόγο των όγκων κανονικού τετραέδρου ακμής α και κανονικής εξαγωνικής πυραμίδας πλευράς α και ύψους α.
9. Επίπεδο παράλληλο στη βάση κανονικής εξαγωνικής πυραμίδας, με πλευρά α και ύψος υ, διχοτομεί το ύψος της. Να υπολογίσετε το εμβαδόν της παράπλευρης επιφάνειας και τον όγκο της κόλουρης πυραμίδας που προκύπτει.

Κ Ε Φ Α Λ Α Ι Ο 13. Σ Τ Ε Ρ Ε Α Σ Χ Η Μ Α Τ Α

Αποδεικτικές Ασκήσεις

1. Δίνεται το παραλληλεπίπεδο ΑΒΓΑ-Α'Β'ΓΆ'. Να αποδείξετε ότι το τετράεδρο ΑΓΒ'Δ' έχει το ένα τρίτο του όγκου του παραλληλεπιπέδου.

Μικροπείραμα

2. Να αποδείξετε ότι σε κάθε τετράεδρο, το γινόμενο του εμβαδού κάθε έδρας επί το αντίστοιχο ύψος είναι σταθερό.

Μικροπείραμα

3. Να αποδείξετε ότι ο όγκος τετραέδρου δε μεταβάλλεται αν μία ακμή μετακινηθεί στο φορέα της χωρίς να αλλάξει μήκος.

Μικροπείραμα

4. Αν δύο τετράεδρα έχουν κοινή μία ακμή και τη δίεδρη που αντιστοιχεί σε αυτήν, τότε ο λόγος των εμβαδών ισούται με το λόγο του γινομένου των εμβαδών των δύο εδρών που πρόσκεινται στη δίεδρη.

Μικροπείραμα

5. Αν δύο τετράεδρα έχουν κοινή μία τρίεδρη γωνία, τότε ο λόγος των όγκων τους ισούται με το λόγο του γινομένου των ακμών της τρίεδρης.

Μικροπείραμα

6. Αν Α', Β', Γ' είναι τα μέσα των ακμών ΟΑ, ΟΒ, ΟΓ τετραέδρου ΟΑΒΓ, τότε (ΟΑ'Β'Γ') = 18 (ΟΑΒΓ).
7. Κανονική τριγωνική πυραμίδα Ο.ΑΒΓ έχει πλευρά βάσης α και οι παράπλευρες ακμές της σχηματίζουν γωνία 60° με τη βάση. Να υπολογίσετε τον όγκο της. Σύνθετα Θέματα

1. Να αποδείξετε ότι ο όγκος τετραέδρου ισούται με το γινόμενο της προβολής του σε επίπεδο κάθετο σε μία ακμή επί το ένα τρίτο της ακμής αυτής.

Μικροπείραμα

2. Αν η κάθετη τομή τριγωνικού πρίσματος έχει ίσες πλευρές, τότε το άθροισμα των αποστάσεων κάθε εσωτερικού σημείου από τις βάσεις και από τις παράπλευρες έδρες είναι σταθερό.
3. Να αποδείξετε ότι το στερεό που έχει κορυφές τα μέσα των ακμών ενός κύβου έχει ίσες ακμές και να υπολογίσετε τον όγκο του

Μικροπείραμα Μικροπείραμα

Μικροπείραμα- Θέμα 1
Μικροπείραμα- Θέμα 2
Μικροπείραμα- Θέμα 3
Μικροπείραμα- Θέμα 4

ΑΝΑΚΕΦΑΛΑΙΩΣΗ

1. Αν τυχαία πυραμίδα τμηθεί με επίπεδο παράλληλο στη βάση της (σχ.29), έχουμε:

• KAKA' = KBKB' = ΚΓΚΓ' = ΚΗΚ'Η' = λ και

• ΑΒΓ ≈ Α'Β'Γ' με λόγο ομοιότητας λ.

2. Μέτρηση κανονικής πυραμίδας:
• Εμβαδόν παράπλευρης επιφάνειας: Ε_π = τ • μ
• Όγκος: V = B•υ3 ,
όπου μ το απόστημα, τ η ημιπερίμετρος της βάσης, υ το ύψος της πυραμίδας και Β το εμβαδόν της βάσης.

3. Μέτρηση κόλουρης πυραμίδας
• Εμβαδόν παράπλευρης επιφάνειας: Ε_π= (τ+τ') • υ'
• Όγκος: $\dfrac{υ \cdot (Β + β +\sqrt{Ββ})}{3}$,
τ και τ' οι ημιπερίμετροι των βάσεων, Β και β τα εμβαδά των βάσεων, υ το ύψος και υ' το παράπλευρο ύψος της πυραμίδας.

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

13.10 Στερεά εκ περιστροφής

Τα στερεά εκ περιστροφής είναι η δεύτερη οικογένεια στερεών που θα μελετήσουμε σε αυτό το κεφάλαιο. Τα στερεά αυτά είναι χρήσιμα τόσο από θεωρητική όσο και από πρακτική άποψη γιατί κατασκευάζονται εύκολα με τη χρήση ειδικών μηχανημάτων. Τα στερεά εκ περιστροφής λέγονται έτσι γιατί δημιουργούνται κατά την περιστροφή μιας επίπεδης γραμμής γύρω από άξονα περιστροφής μία ευθεία που βρίσκεται στο επίπεδο της γραμμής (σχ.30). Τα σημεία της γραμμής αυτής κατά την περιστροφή γράφουν κύκλους που βρίσκονται σε επίπεδα κάθετα στον άξονα περιστροφής και έχουν τα κέντρα τους στον άξονα. Στις επόμενες παραγράφους θα μελετήσουμε τον κύλινδρο, τον κώνο και τη σφαίρα ως στερεά εκ περιστροφής.

Μικροπείραμα

Κύλινδρος

13.11 Ορισμός και στοιχεία κυλίνδρου

Ορισμός
Ορθός κύλινδρος ή κύλινδρος εκ περιστροφής ή κύλινδρος λέγεται το σχήμα που παράγεται από ένα ορθογώνιο παραλληλόγραμμο, το οποίο εκτελεί μία πλήρη περιστροφή στο χώρο γύρω από τη μία πλευρά του.

Το ευθύγραμμο τμήμα Α'Β' γύρω από το οποίο περιστρέφεται το παραλληλόγραμμο ΑΒΒ'Α' (σχ.31), μένει αμετακίνητο κατά την περιστροφή, λέγεται άξονας ή ύψος του κυλίνδρου. Κατά την περιστροφή, η πλευρά ΑΒ παραμένει παράλληλη και σε σταθερή απόσταση από τον άξονα Α'Β' και η τυχαία θέση της πλευράς ΑΒ λέγεται γενέτειρα του κυλίνδρου. Η επιφάνεια που δημιουργείται από την κίνηση της πλευράς ΑΒ λέγεται παράπλευρη ή κυρτή επιφάνεια του κυλίνδρου.

Οι πλευρές Α'Α και Β'Β του παραλληλογράμμου, ως κάθετες στην Α'Β' και ίσες μεταξύ τους, κατά την περιστροφή, γράφουν ίσους και παράλληλους κυκλικούς δίσκους που ανήκουν σε επίπεδα κάθετα στον άξονα στα σημεία Α' και Β'. Οι κύκλοι (Α',Α'Α) και (Β', Β'Β) είναι παράλληλοι, λέγονται βάσεις του κυλίνδρου και η ακτίνα Α'Α = Β'Β λέγεται ακτίνα του κυλίνδρου.

Ο κύλινδρος θα συμβολίζεται με (Α'Β', Α'Α), όπου Α'Β' είναι ο άξονας του κυλίνδρου και Α'Α είναι η ακτίνα του.

Μικροπείραμα

Σχήμα 30

Σχήμα 31

Κ Ε Φ Α Λ Α Ι Ο 13. Σ Τ Ε Ρ Ε Α Σ Χ Η Μ Α Τ Α

Σχήμα 32

Σχήμα 33

Σχήμα 34

13.12 Μέτρηση κυλίνδρου

Έστω κύλινδρος (ΑΑ',ρ). Αν στη μία βάση του κυλίνδρου (σχ.32) εγγράψουμε ένα πολύγωνο και από τις κορυφές του πολυγώνου φέρουμε ευθύγραμμα τμήματα παράλληλα και ίσα με τον άξονα του κυλίνδρου, τα τμήματα αυτά είναι γενέτειρες του κυλίνδρου, οι οποίες ξεκινάνε από σημεία της μίας βάσης, βρίσκονται στην κυρτή επιφάνεια του κυλίνδρου και καταλήγουν στην άλλη βάση ως κορυφές ενός πολυγώνου, ίσου και παράλληλου στο αρχικό πολύγωνο. Σχηματίζεται έτσι ένα ορθό πρίσμα που λέγεται εγγεγραμμένο στον κύλινδρο.

Μικροπείραμα

Αν στη μία βάση του κυλίνδρου (ΒΒ',ρ) , περιγράψουμε ένα πολύγωνο (σχ.33) και από τις κορυφές του πολυγώνου φέρουμε ευθύγραμμα τμήματα παράλληλα και ίσα με τον άξονα του κυλίνδρου ΒΒ', σχηματίζεται ένα ορθό πρίσμα, οι έδρες του οποίου είναι επίπεδα εφαπτόμενα στον κύλινδρο κατά μήκος γενετειρών και οι βάσεις του είναι ίσα πολύγωνα περιγεγραμμένα στις δύο βάσεις. Ένα τέτοιο πρίσμα λέγεται περιγεγραμμένο στον κύλινδρο.

Μικροπείραμα

• Ανάπτυγμα του κυλίνδρου
Εγγράφουμε στον κύλινδρο (ΑΑ', ρ), ένα κανονικό πρίσμα, το οποίο αναπτύσσουμε στο επίπεδο (σχ. 32). Το ανάπτυγμα του πρίσματος είναι ένα ορθογώνιο με το ένα ζεύγος απέναντι πλευρών ίσες με τις γενέτειρες και το άλλο ίσο με την περίμετρο της βάσης του πρίσματος. Αν διπλασιάζουμε συνεχώς τον αριθμό των πλευρών του πρίσματος, η περίμετρος της βάσης του τείνει στο μήκος του κύκλου. Άρα, στο όριο, το ανάπτυγμα της κυρτής επιφάνειας του κυλίνδρου είναι ορθογώνιο με πλευρές τη γενέτειρα και το μήκος του κύκλου της βάσης, δηλαδή υ και 2ρπ αντίστοιχα, όπου υ το ύψος ρ η ακτίνα του κυλίνδρου (σχ.34). Το ανάπτυγμα της ολικής επιφάνειας αποτελείται από το ορθογώνιο παραλληλόγραμμο ΚΛΜΝ που περιγράψαμε και από δύο κυκλικούς δίσκους ακτίνας ρ, που αντιστοιχούν στις δύο βάσεις του κυλίνδρου (σχ.34).

Μικροπείραμα

• Εμβαδόν επιφάνειας κυλίνδρου
Σύμφωνα με τους συλλογισμούς που κάναμε για την κατασκευή του αναπτύγματος, προκύπτει αμέσως το ακόλουθο θεώρημα:

ΘΕΩΡΗΜΑ Ι

Το εμβαδόν της κυρτής και της ολικής επιφάνειας ενός κυλίνδρου ακτίνας ρ και ύψους υ είναι Ε_κ=2πρυ και Ε₀=2πρ(υ+ρ) αντίστοιχα.

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

• Όγκος κυλίνδρου
Αν εγγράψουμε στον κύλινδρο ένα ορθό κανονικό πρίσμα με βάση κανονικό ν-γωνο, ο όγκος του πρίσματος ισούται με το εμβαδόν της βάσης επί το ύψος του. Θεωρούμε τώρα ότι το ν διπλασιάζεται συνεχώς, ώστε το πλήθος των πλευρών της βάσης του πρίσματος να τείνει στο άπειρο, οπότε το εμβαδόν της βάσης τείνει στο εμβαδόν του κύκλου. Τότε, στο όριο, ο όγκος του κυλίνδρου ισούται με το εμβαδόν του κύκλου της βάσης επί το ύψος, δηλαδή:

ΘΕΩΡΗΜΑ ΙI

Ο όγκος κυλίνδρου ύψους υ και ακτίνας ρ ισούται με V=πρ²υ.

ΠΑΡΑΤΗΡΗΣH
Αν αντί των εγγεγραμμένων πρισμάτων στον κύλινδρο χρησιμοποιούσαμε τα περιγεγραμμένα θα βρίσκαμε τους ίδιους ακριβώς τύπους για την επιφάνεια και τον όγκο του κυλίνδρου.

ΑΣΚΗΣΕΙΣ ΓΙΑ ΛΥΣΗ

Ασκήσεις Εμπέδωσης

1. Να υπολογίσετε το εμβαδόν της κυρτής και ολικής επιφάνειας και τον όγκο του κυλίνδρου που έχει ύψος 1 και ακτίνα 1.
2. Το ίδιο για κύλινδρο με ακτίνα 15 και ύψος 8.
3. Να υπολογίσετε τον όγκο, την κυρτή και τη συνολική επιφάνεια κυλίνδρου που έχει ύψος διπλάσιο της ακτίνας του.
4. Κυλινδρική δεξαμενή έχει ακτίνα 1μ. Να υπολογίσετε τη χωρητικότητα σε λίτρα της δεξαμενής για κάθε εκατοστό του μέτρου ύψος.
5. Το εμβαδόν της ολικής επιφάνειας ενός κυλίνδρου με ύψος 2 είναι ίσο με το εμβαδόν κύκλου ακτίνας 4. Να βρεθεί η ακτίνα ρ του κυλίνδρου.

Αποδεικτικές Ασκήσεις

1. Κύλινδρος έχει όγκο V και ύψος υ. Να υπολογίσετε την ολική του επιφάνεια.
2. Θεωρούμε τετράγωνο ΑΒΓΔ πλευράς α και Μ το μέσο του ΑΒ. Να υπολογίσετε τον όγκο του στερεού που σχηματίζεται από το ορθογώνιο ΜΝΓΒ, (ΜΝ//ΑΔ) κατά την περιστροφή του γύρω από την πλευρά ΑΔ. Σε ποια θέση πρέπει να είναι το Μ, ώστε ο παραγόμενος όγκος να είναι το μισό του κυλίνδρου που παράγεται από το τετράγωνο;

Μικροπείραμα

3. Θεωρούμε ορθογώνιο ΑΒΓΔ που περιστρέφεται γύρω από άξονα του επιπέδου του που δεν το τέμνει και είναι παράλληλος στη πλευρά ΑΒ. Να υπολογίσετε τον όγκο και την ολική επιφάνεια που παράγεται από το ορθογώνιο και να αποδείξετε ότι ισούται με το μήκος του κύκλου που γράφει το κέντρο Ο του ορθογωνίου επί το εμβαδόν και την περίμετρο του ορθογωνίου αντίστοιχα.

Μικροπείραμα

ΑΝΑΚΕΦΑΛΑΙΩΣΗ

1. Εμβαδόν επιφάνειας κυλίνδρου:

κυρτής: Ε_Κ = 2πρυ,

ολικής: Ε_ο=2πρ(υ+ρ)

2. Όγκος κυλίνδρου: V=πρ²υ.

Κ Ε Φ Α Λ Α Ι Ο 13. Σ Τ Ε Ρ Ε Α Σ Χ Η Μ Α Τ Α

Σχήμα 35

Σχήμα 36

Σχήμα 37

Κώνος

13.13 Ορισμός και στοιχεία κώνου

Ορισμός
Ορθός κώνος ή κώνος εκ περιστροφής ή απλώς κώνος λέγεται το στερεό σχήμα που παράγεται από την περιστροφή ενός ορθογώνιου τριγώνου γύρω από μία κάθετη πλευρά του.

Μικροπείραμα

Θεωρούμε ένα ορθογώνιο τρίγωνο ΚΟΑ, με την ορθή γωνία στο Ο (σχ.35), το οποίο περιστρέφεται γύρω από την κάθετη πλευρά ΚΟ. Η υποτείνουσα ΚΑ του ορθογώνιου τριγώνου, κατά την περιστροφή, διέρχεται από το σταθερό σημείο Κ και γράφει μία κυρτή επιφάνεια, ενώ η κάθετη πλευρά ΟΑ γράφει έναν κυκλικό δίσκο κέντρου Ο και ακτίνας ΟΑ, που βρίσκονται στο επίπεδο που είναι κάθετο στην ΚΟ στο Ο. Το στερεό σχήμα που παράγεται με αυτόν τον τρόπο από το τρίγωνο ΚΟΑ λέγεται κώνος. Η κυρτή επιφάνεια που παράγεται από την υποτείνουσα ΚΑ λέγεται παράπλευρη ή κυρτή επιφάνεια του κώνου, η τυχαία θέση της ΚΑ λέγεται γενέτειρα ή πλευρά του κώνου. Η κάθετη πλευρά ΚΟ, που παραμένει σταθερή κατά την περιστροφή, λέγεται άξονας ή ύψος, το σημείο Κ λέγεται κορυφή, ο κύκλος που γράφει η κάθετη πλευρά ΟΑ λέγεται βάση και η ακτίνα της βάσης λέγεται ακτίνα του κώνου. Είναι προφανές ότι όλες οι γενέτειρες ενός κώνου είναι ίσες. Ο κώνος συμβολίζεται με (ΚΟ, ΟΑ), όπου ΚΟ ο άξονας και ΟΑ η ακτίνα της βάσης του κώνου.

13.14 Μέτρηση του κώνου

Θεωρούμε έναν κώνο (ΚΟ,ρ) (σχ.36), και ένα πολύγωνο εγγεγραμμένο στη βάση του κώνου, π.χ. ένα τετράπλευρο ΑΒΓΔ. Αν ενώσουμε την κορυφή Κ του κώνου με τις κορυφές του πολυγώνου, οι ακμές της πυραμίδας είναι γενέτειρες του κώνου. Η πυραμίδα λοιπόν που έχει με τον κώνο κοινή κορυφή και η βάση της είναι εγγεγραμμένη στη βάση του κώνου λέγεται εγγεγραμμένη στον κώνο.

Μικροπείραμα

Αν τώρα θεωρήσουμε ένα πολύγωνο, περιγεγραμμένο στη βάση ενός κώνου, πχ ένα τετράπλευρο ΑΒΓΔ (σχ.37) και συνδέσουμε

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

την κορυφή Κ του κώνου με τις κορυφές του πολυγώνου, προκύπτει μία πυραμίδα που λέγεται περιγεγραμμένη στον κώνο. Η πυραμίδα αυτή έχει έδρες που εφάπτονται στην κυρτή επιφάνεια του κώνου κατά μήκος γενετειρών.

Μικροπείραμα

• Ανάπτυγμα του κώνου
Η κυρτή επιφάνεια ενός κώνου μπορεί να αναπτυχθεί στο επίπεδο. Για το σκοπό αυτό εγγράφουμε στον κώνο (ΚΟ,ρ) (σχ.38), μία κανονική ν-γωνική πυραμίδα, την οποία στη συνέχεια αναπτύσσουμε στο επίπεδο. Το ανάπτυγμα της παράπλευρης επιφάνειας της κανονικής πυραμίδας αποτελείται από ν ίσα ισοσκελή τρίγωνα (σχ.39), τα οποία κατασκευάζουμε το ένα δίπλα στο άλλο ως εγγεγραμμένα τρίγωνα στον κύκλο (Κ',λ), όπου Κ' τυχόν σημείο του επιπέδου και λ το μήκος της γενέτειρας του κώνου.

Διπλασιάζοντας συνεχώς τον αριθμό ν των κορυφών της εγγεγραμμένης πυραμίδας, τα μήκη των ίσων χορδών ΑΒ, ΒΓ, κτλ. γίνονται συνεχώς μικρότερα και η πολυγωνική γραμμή Α'Β'...Α' στο ανάπτυγμα τείνει να συμπέσει με το τόξο του κύκλου (Κ',λ). Στο όριο λοιπόν, το ανάπτυγμα του κώνου είναι ένας τομέας του κύκλου (Κ', λ), το τόξο του οποίου έχει μήκος ΑA'=2πρ. Αν ονομάσουμε φ τη γωνία Α'K'Α' του τομέα, μετρημένη σε μοίρες, έχουμε τη σχέση (σχ.40):

εικόνα

Άρα, το ανάπτυγμα της κυρτής επιφάνειας κώνου με πλευρά λ και ακτίνα ρ είναι τομέας κύκλου ακτίνας λ που βλέπει τόξο μήκους 2πρ ή σε μοίρες:

Μικροπείραμα

• Εμβαδόν επιφάνειας και όγκος του κώνου
Σύμφωνα με τους συλλογισμούς που κάναμε για την κατασκευή του αναπτύγματος, προκύπτει αμέσως το ακόλουθο Θεώρημα.

ΘΕΩΡΗΜΑ Ι

Το εμβαδόν της κυρτής Ε_κ και της ολικής Ε_ο επιφάνειας ενός κώνου με ακτίνα ρ και γενέτειρα λ, ισούται με:

Ε_κ=πρλ και Ε₀=πρ(ρ+λ).

Σχήμα 38

Σχήμα 39

Σχήμα 40

Κ Ε Φ Α Λ Α Ι Ο 13. Σ Τ Ε Ρ Ε Α Σ Χ Η Μ Α Τ Α

ΠΑΡΑΤΗΡΗΣH
Αντί των εγγεγραμμένων πυραμίδων μπορούμε να χρησιμοποιήσουμε τις περιγεγραμμένες. Ο όγκος του κώνου είναι μικρότερος από τον όγκο των περιγεγραμμένων πυραμίδων και μεγαλύτερος των εγγεγραμμένων.

Σχήμα 41

ΑΠΟΔΕΙΞΗ

Το ανάπτυγμα της κυρτής επιφάνειας του κώνου είναι τομέας κύκλου ακτίνας λ που έχει μήκος τόξου 2πρ. Για το εμβαδόν Ε_κ αυτού του τομέα ισχύει η σχέση:

Το εμβαδόν της ολικής επιφάνειας προκύπτει αν στο εμβαδόν της παράπλευρης επιφάνειας προσθέσουμε το εμβαδόν της βάσης του κώνου, δηλαδή:

Ε₀ = πρ² + πρλ = πρ (ρ + λ).

ΘΕΩΡΗΜΑ ΙΙ

Ο όγκος κώνου ακτίνας ρ και ύψους υ ισούται με:

V = πρ² υ3 .

ΑΠΟΔΕΙΞΗ

Θεωρούμε κανονική πυραμίδα εγγεγραμμένη στον κώνο, η οποία έχει όγκο V = Β•υ3 , όπου Β το εμβαδόν της βάσης της. Αν ο αριθμός των πλευρών της πυραμίδας συνεχώς διπλασιάζεται, τότε στο όριο, το εμβαδόν της βάσης της πυραμίδας είναι το εμβαδόν της βάσης του κώνου και ο όγκος του κώνου ισούται με V = πρ²υ3 .

13.15 Κόλουρος κώνος

Έστω κώνος (ΚΟ, ρ), ο οποίος τέμνει ένα επίπεδο κάθετο στον άξονά του στο σημείο Ο' μεταξύ Κ και Ο (σχ. 41). Δημιουργείται έτσι ένας μικρότερος κώνος, με την ίδια κορυφή και βάση έναν κύκλο παράλληλο προς τον αρχικό, με μικρότερη ακτίνα, ο οποίος αφαιρείται από τον αρχικό κώνο.

Το σχήμα που απομένει λέγεται κόλουρος κώνος και αποτελείται από το μέρος του κώνου που περιλαμβάνεται μεταξύ της βάσης και ενός επιπέδου παράλληλου σε αυτό, μεταξύ κορυφής και βάσης. Οι δύο παράλληλοι κύκλοι λέγονται βάσεις του κόλουρου κώνου (μικρή και μεγάλη) και το ευθύγραμμο τμήμα ΟΟ' που συνδέει τα κέντρα των βάσεων λέγεται άξονας ή ύψος. Το τμήμα ΑΑ' λέγεται γενέτειρα ή πλευρά.

Για τον όγκο και την επιφάνεια ενός κόλουρου κώνου ισχύουν τα επόμενα Θεωρήματα.

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

ΘΕΩΡΗΜΑΤΑ

Το εμβαδόν της κυρτής Ε_κ και της ολικής Ε_ο επιφάνειας κόλουρου κώνου με ακμή λ και ακτίνες βάσεων ρ και ρ', ισούται με:

Ε_κ=πλ(ρ+ρ) και Ε₀=πλ(ρ+ρ')+π(ρ²+ρ'²).

Ο όγκος κόλουρου κώνου, με ύψος υ και ακτίνες ρ και ρ', ισούται με:

V = πυ3(ρ²+ρ'²+ρρ').

ΑΣΚΗΣΕΙΣ ΓΙΑ ΛΥΣΗ

Ασκήσεις Εμπέδωσης

1. Κώνος έχει ακτίνα 3 και ύψος 4. Να υπολογίσετε τον όγκο, την κυρτή και την ολική επιφάνεια του κώνου.
2. Κώνος έχει ύψος 4 και επιφάνεια 6π. Να βρείτε την ακτίνα του κώνου.
3. Κατασκευάζεται αποθήκη οικοδομικών υλικών σε σχήμα αντεστραμμένου κώνου (σιλό), χωρίς κάλυμμα, με ακτίνα βάσης ρ και γενέτειρα 2ρ. Να υπολογίσετε το εμβαδόν της λαμαρίνας που χρειάζεται για την κατασκευή της και τον όγκο της αποθήκης.
4. Κώνος παράγεται από την περιστροφή ορθογώνιου και ισοσκελούς τριγώνου γύρω από το ύψος του. Αν ρ είναι η ακτίνα της βάσης του κώνου, να υπολογίσετε τον όγκο και την κυρτή επιφάνεια του κώνου.
5. Το εμβαδόν της ολικής επιφάνειας κώνου είναι ίσο με το εμβαδόν κύκλου ακτίνας α. Να βρείτε την κυρτή επιφάνεια και τον όγκο του κώνου, αν έχει ακτίνα ρ.
6. Να βρείτε το λόγο του εμβαδού της βάσης ενός κώνου προς το εμβαδόν της κυρτής επιφάνειάς του, αν έχει ύψος ίσο με την διάμετρο της βάσης του.
7. Κώνος και κύλινδρος έχουν ίσες βάσεις και ίσα ύψη. Να βρείτε το λόγο των κυρτών επιφανειών τους.
8. Να βρείτε τη γωνία του κυκλικού τομέα που παριστάνει το ανάπτυγμα του κώνου ακτίνας ρ και ύψους $υ = \sqrt{15}ρ.$

Αποδεικτικές Ασκήσεις

1. Να χωριστεί η κυρτή επιφάνεια κώνου σε δύο ισοδύναμα μέρη με επίπεδο κάθετο στον άξονα του κώνου. Το ίδιο για τους όγκους των κώνων.
2. Ισοπλεύρου τριγώνου ΑΒΓ προεκτείνουμε την πλευρά ΑΒ κατά ίσο μήκος και στο σημείο αυτό φέρουμε ευθεία ξ κάθετη στην ΑΒ. Να υπολογίσετε τον όγκο που παράγεται από το ισόπλευρο τρίγωνο, αν αυτό περιστραφεί γύρω από την ευθεία ξ.

Μικροπείραμα

3. Κώνος έχει ακτίνα ρ και γενέτειρα 2ρ. Να χωρίσετε τον κώνο με δύο παράλληλα επίπεδα στη βάση σε τρία μέρη, ώστε οι κυρτές επιφάνειες που προκύπτουν να είναι ισοδύναμες.
4. Να αποδείξετε ότι ο όγκος ενός κώνου ισούται με το εμβαδόν του ορθογώνιου τριγώνου που τον παράγει επί το 13 του μήκους του κύκλου της βάσης.
5. Να αποδείξετε ότι τα εμβαδά των κυρτών επιφανειών δύο κώνων που παράγονται από δύο όμοια ορθογώνια τρίγωνα είναι ανάλογα προς τα τετράγωνα των ακτίνων τους.
6. Το εμβαδόν της κυρτής επιφάνειας ενός κώνου ισούται με το εμβαδόν κύκλου ακτίνας α. Να υπολογίσετε: i) τον όγκο του κώνου, αν έχει ακτίνα ρ και ii) τον όγκο του κώνου, αν α = 1 και ρ = 23 .

Κ Ε Φ Α Λ Α Ι Ο 13. Σ Τ Ε Ρ Ε Α Σ Χ Η Μ Α Τ Α

ΑΝΑΚΕΦΑΛΑΙΩΣΗ

1. Εμβαδόν επιφάνειας κώνου ακτίνας ρ και γενέτειρας λ:

κυρτής: Ε_κ=πρλ,
ολικής: Ε_ο=πρ(ρ+λ).

2. Το ανάπτυγμα κώνου ακτίνας ρ και γενέτειρας λ είναι κυκλικός τομέας γωνίας:
φ = ρλ ∙ 360° .

3. Όγκος κώνου ύψους υ και ακτίνας ρ : V = πρ²υ3 .

4. Κόλουρος κώνος με ακτίνες ρ, ρ', ύψος υ και γενέτειρα λ:

εμβαδόν κυρτής επιφάνεια Ε_κ=πλ(ρ+ρ')
εμβαδόν ολικής επιφάνειας Ε_ο = πλ(ρ + ρ') + π(ρ² + ρ'²)
όγκος V = πυ3 (ρ²+ρ'²+ρρ').

Σχήμα 42

Σχήμα 43

Σφαίρα

13.16 Ορισμός και στοιχεία σφαίρας

Η σφαίρα, ένα στερεό σχήμα που είναι γνωστό από την εποπτεία, μπορεί να οριστεί γεωμετρικά με δύο τρόπους. Κατά τον ένα τρόπο, θεωρείται ότι προκύπτει ως επιφάνεια εκ περιστροφής, ενώ κατά τον δεύτερο τρόπο ότι είναι γεωμετρικός τόπος σημείων του χώρου. Ακολουθούν και οι δύο ορισμοί:

Ορισμοί
i) Σφαίρα είναι το σχήμα που παράγεται από την περιστροφή ενός κύκλου (Ο, ρ) με άξονα περιστροφής μία διάμετρό του.

Μικροπείραμα

ii) Σφαίρα είναι το σύνολο των σημείων του χώρου που απέχουν από ένα σταθερό σημείο Ο σταθερή απόσταση ρ.

Το σημείο Ο λέγεται κέντρο (σχ.42) και το τμήμα ΟΒ = ρ λέγεται ακτίνα της σφαίρας. Η σφαίρα συμβολίζεται με (Ο,ρ), όπου Ο είναι το κέντρο της σφαίρας και ρ η ακτίνα της. Κάθε ευθεία που περνάει από το κέντρο Ο της σφαίρας τέμνει τη σφαίρα σε δύο σημεία Α και Α', τα οποία λέγονται αντιδιαμετρικά σημεία (σχ.43) και το ευθύγραμμο τμήμα ΑΑ' λέγεται διάμετρος της σφαίρας. Το ευθύγραμμο τμήμα ΑΒ που ενώνει δύο τυχαία σημεία της σφαίρας λέγεται χορδή. Τα σημεία του

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

χώρου που απέχουν από το κέντρο της σφαίρας απόσταση μικρότερη από την ακτίνα της σφαίρας λέγονται εσωτερικά σημεία της σφαίρας, ενώ εκείνα των οποίων η απόσταση από το κέντρο είναι μεγαλύτερη από την ακτίνα λέγονται εξωτερικά. Ως άμεση συνέπεια του ορισμού προκύπτουν οι εξής προτάσεις:

ΠΡΟΤΑΣΕΙΣ

Κάθε σφαίρα έχει μόνο ένα κέντρο Ο.
Όλες οι διάμετροι της σφαίρας είναι ίσες.
Κάθε χορδή σφαίρας είναι μικρότερη από τη διάμετρο.
Αν ΑΒ είναι χορδή σφαίρας και Μ το μέσο της χορδής, τότε η ΟΜ είναι κάθετη στη χορδή.

ΠΡΟΤΑΣΗ

Τέσσερα σημεία του χώρου, που δεν ανήκουν στο ίδιο επίπεδο, ορίζουν μοναδική σφαίρα.

ΑΠΟΔΕΙΞΗ

Θεωρούμε τα σημεία Α, Β, Γ και Δ, που δεν ανήκουν στο ίδιο επίπεδο. Τα σημεία της ευθείας ξ που είναι κάθετη στο επίπεδο του τριγώνου ΑΒΓ στο περίκεντρο Κ ισαπέχουν από τα Α, Β και Γ (σχ.44). Κατασκευάζουμε τώρα το επίπεδο π που είναι μεσοκάθετο στο ευθύγραμμο τμήμα ΑΔ, που τέμνει την ευθεία ξ σε ένα σημείο Ο. Το σημείο Ο ισαπέχει και από τα τέσσερα σημεία Α, Β, Γ και Δ. Τέλος, επειδή το κέντρο κάθε σφαίρας που διέρχεται από τα σημεία Α, Β και Γ είναι σημείο της ξ και το κέντρο κάθε σφαίρας που διέρχεται από τα Α και Δ είναι σημείο του π, έπεται ότι η σφαίρα αυτή είναι μοναδική.

Μικροπείραμα

13.17 Θέσεις ευθείας και επιπέδου ως προς σφαίρα

• Σχετική θέση επιπέδου και σφαίρας
Έστω σφαίρα (Ο,ρ), επίπεδο π που απέχει απόσταση ΟΚ=δ από το κέντρο Ο της σφαίρας (σχ.45).

i) Αν δ > ρ (σχ. 45α), τότε όλα τα σημεία του επιπέδου είναι εξωτερικά σημεία της σφαίρας, επομένως το επίπεδο και η σφαίρα δεν έχουν κοινά σημεία.

ii) Αν δ = ρ (σχ. 45β), τότε το σημείο Κ είναι κοινό σημείο της σφαίρας και του επιπέδου, ενώ κάθε άλλο σημείο του επιπέδου είναι εξωτερικό σημείο της σφαίρας. Τότε το επίπεδο λέγεται εφαπτόμενο επίπεδο της σφαίρας και το σημείο Κ λέγεται σημείο επαφής.

Σχήμα 44

Σχήμα 45

Κ Ε Φ Α Λ Α Ι Ο 13. Σ Τ Ε Ρ Ε Α Σ Χ Η Μ Α Τ Α

Σχήμα 46

Σχήμα 47

Σχήμα 47

iii) Αν δ < ρ (σχ. 45γ), τότε το σημείο Κ είναι εσωτερικό σημείο της σφαίρας. Τότε το επίπεδο τέμνει την σφαίρα και η τομή είναι κύκλος του επιπέδου π με κέντρο το σημείο Κ και ακτίνα ρ' =

Μικροπείραμα

Όταν το επίπεδο περνάει από το κέντρο της σφαίρας, τότε η τομή της σφαίρας με το επίπεδο είναι κύκλος που έχει κέντρο Ο και ακτίνα ρ και λέγεται μέγιστος κύκλος. Η τομή της σφαίρας με επίπεδο που δεν περνάει από το κέντρο λέγεται μικρός κύκλος της σφαίρας.

• Σχετική θέση ευθείας και σφαίρας
Θεωρούμε σφαίρα (Ο, ρ) και ευθεία ε που δε διέρχεται από το κέντρο Ο. Στο επίπεδο (Ο, ε) γράφουμε τον κύκλο (Ο,ρ), που είναι μέγιστος κύκλος της σφαίρας και έστω ΟΚ = δ η απόσταση του σημείου Ο από την ευθεία ε. Η εύρεση των κοινών σημείων της ευθείας και της σφαίρας ανάγεται στην εύρεση των κοινών σημείων της ευθείας ε και του κύκλου (Ο,ρ).
i) Έστω ότι δ < ρ (σχ.46α). Τότε η ευθεία ε τέμνει τον κύκλο (Ο,ρ) σε δύο σημεία Μ και Ν. Άρα η ευθεία ε τέμνει τη σφαίρα σε δύο σημεία, τα Μ και Ν.
ii) Έστω ότι δ = ρ (σχ.46β). Τότε ο κύκλος (Ο,ρ) που βρίσκεται στο επίπεδο (Ο, ε), εφάπτεται στην ευθεία ε και το σημείο Κ είναι το μοναδικό κοινό σημείο της ευθείας ε και της σφαίρας (Ο,ρ). Στην περίπτωση αυτή η ευθεία ε λέγεται εφαπτομένη της σφαίρας και σημείο Κ λέγεται σημείο επαφής.
iii) Έστω ότι δ > ρ (σχ. 46γ). Ο κύκλος (Ο,ρ) δεν τέμνει την ευθεία ε, επομένως η ευθεία και η σφαίρα δεν έχουν κοινά σημεία. Αν η ευθεία ε διέρχεται από το Ο, τότε η ε τέμνει τη σφαίρα σε δύο αντιδιαμετρικά σημεία.

Μικροπείραμα

13.18 Μέτρηση σφαίρας

• Εμβαδόν και όγκος παραγόμενος από την περιστροφή επίπεδης πολυγωνικής γραμμής
Για το υπολογισμό του εμβαδού της επιφάνειας της σφαίρας και του όγκου της θα χρειαστούμε τα επόμενα θεωρήματα που αναφέρονται ως θεωρήματα του Πάππου. Ο Πάππος έζησε τον 3ο μ.Χ. αιώνα και εδίδαξε στο Πανεπιστήμιο της Αλεξάνδρειας.

ΘΕΩΡΗΜΑ Ι

Το εμβαδόν της επιφάνειας που παράγεται κατά την πλήρη περιστροφή ενός ευθύγραμμου τμήματος ΑΒ (σχ.47), με άξονα περιστροφής ευθεία ξ συνεπίπεδη με το τμήμα, που δεν το τέμνει σε εσωτερικό σημείο και δεν είναι κάθετη σε αυτό, ισούται με το γινόμενο του κύκλου που έχει ακτίνα το τμήμα ΜΝ που είναι κάθετο στο μέσο του ευθύγραμμου τμήματος μέχρι τον άξονα, επί το μήκος της προβολής Α'Β' του τμήματος στον άξονα, δηλαδή

εμβ(ΑΒ) = 2π •ΜΝ • Α'Β'.

Μικροπείραμα

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

ΘΕΩΡΗΜΑ ΙΙ

Ο όγκος του στερεού που παράγεται κατά την περιστροφή τριγώνου ΑΒΓ γύρω από άξονα ξ, που ανήκει στο επίπεδο του τριγώνου και διέρχεται από την κορυφή Α, χωρίς να το τέμνει σε εσωτερικά σημεία, ισούται με το γινόμενο του εμβαδού της επιφάνειας που παράγει η πλευρά ΒΓ επί το ένα τρίτο του ύψους που αντιστοιχεί στην κορυφή Α του τριγώνου (σχ.48), δηλαδή:

ογκ(ΑΒΓ) = 13 υ • εμβ(ΒΓ).

Μικροπείραμα

• Εμβαδόν επιφάνειας σφαίρας

ΘΕΩΡΗΜΑ ΙΙΙ

Το εμβαδόν της επιφάνειας σφαίρας (Ο,ρ) ισούται με το εμβαδόν τεσσάρων μέγιστων κύκλων, δηλαδή:

Ε=4πρ².

ΑΠΟΔΕΙΞΗ

Θεωρούμε ότι η σφαίρα (Ο,ρ) παράγεται από την περιστροφή ενός μέγιστου κύκλου της, με άξονα μία διάμετρο. Στο μέγιστο κύκλο εγγράφουμε ένα κανονικό πολύγωνο με άρτιο πλήθος κορυφών, π.χ. ένα εξάγωνο (σχ. 49). Κατά την περιστροφή γύρω από τη διάμετρο ΑΔ, η πολυγωνική γραμμή ΑΒΓΔ, σύμφωνα με το θεώρημα I του Πάππου, παράγει επιφάνεια εμβαδού:

Ε₆=2πα₆(ΑΒ'+Β'Γ'+Γ'Δ)=2πα₆ • ΑΔ=4πρα₆,

όπου α₆ είναι το απόστημα του κανονικού εξαγώνου.
Διπλασιάζοντας συνεχώς τις πλευρές του εγγεγραμμένου πολυγώνου, στο όριο, η πλευρά του εγγεγραμμένου πολυγώνου συνεχώς μειώνεται, το πολύγωνο τείνει στο μέγιστο κύκλο και το απόστημα τείνει στην ακτίνα του κύκλου. Στο όριο λοιπόν, έχουμε:

Ε=4πρ•ρ=4πρ².

Σχήμα 48

Σχήμα 48

Σχήμα 49

Σχήμα 49

Κ Ε Φ Α Λ Α Ι Ο 13. Σ Τ Ε Ρ Ε Α Σ Χ Η Μ Α Τ Α

Σχήμα 49α

ΣΧΟΛΙΟ
Ο όγκος και το εμβαδόν της επιφάνειας σφαίρας και ο όγκος και το εμβαδόν της κυρτής επιφάνειας κώνου, κόλουρου κώνου και κυλίνδρου υπολογίστηκαν για πρώτη φορά από τον Αρχιμήδη με διαφορετική μέθοδο από αυτήν που χρησιμοποιούμε εδώ, που την αποκαλούσε «έφοδο».

• Όγκος σφαίρας

ΘΕΩΡΗΜΑ ΙV

Ο όγκος σφαίρας ακτίνας ρ είναι: V = 43 πρ³.

ΑΠΟΔΕΙΞΗ

Εγγράφουμε στον κύκλο που παράγει τη σφαίρα εκ περιστροφής ένα κανονικό πολύγωνο με άρτιο πλήθος κορυφών, π.χ. ένα εξάγωνο (σχ.49α). Κατά την περιστροφή γύρω από τον άξονα ΑΔ, τα τρίγωνα ΟΑΒ, ΟΒΓ και ΟΓΔ παράγουν όγκο, που σύμφωνα με το Θεώρημα II του Πάππου δίνεται από τη σχέση:

εικόνα

όπου α₆ είναι το απόστημα του κανονικού εξαγώνου και εμβ(ΑΒ) είναι το εμβαδόν της επιφάνειας που παράγεται από το τμήμα ΑΒ κατά την περιστροφή του γύρω από τον άξονα ΑΔ. Διπλασιάζοντας συνεχώς τις πλευρές του εγγεγραμμένου πολυγώνου, στο όριο, η πλευρά του εγγεγραμμένου πολυγώνου τείνει στο μηδέν, το εμβαδόν της πολυγωνικής γραμμής ΑΒ...Δ τείνει στο εμβαδόν του ημικυκλίου ακτίνας ρ, το εμβαδόν που παράγει η πολυγωνική γραμμή ΑΒ...Δ τείνει στο εμβαδόν της σφαίρας και το απόστημα τείνει στην ακτίνα ρ του κύκλου. Στο όριο, λοιπόν, έχουμε:

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

ΑΣΚΗΣΕΙΣ ΓΙΑ ΛΥΣΗ

Ασκήσεις Εμπέδωσης

1. Σφαίρα ακτίνας 50 τέμνεται από επίπεδο που απέχει από το κέντρο απόσταση 20. Να υπολογίσετε την ακτίνα της τομής.
2. Σφαίρα ακτίνας 40 τέμνεται από επίπεδο κατά κύκλο με εμβαδόν 900π. Να βρείτε την απόσταση του επιπέδου από το κέντρο της σφαίρας.
3. Διαιρούμε μία ακτίνα σφαίρας (Ο,ρ) σε δύο ίσα τμήματα και από το σημείο της διαίρεσης φέρουμε επίπεδο κάθετο στην ακτίνα. Να υπολογίσετε το εμβαδόν του κύκλου της τομής.
4. Σφαίρα ακτίνας ρ φορτίζεται από φωτεινή πηγή που βρίσκεται σε απόσταση δ>ρ από το κέντρο της σφαίρας. Να βρείτε την ακτίνα του κύκλου που χωρίζει το φωτιζόμενο μέρος της σφαίρας από το σκοτεινό.
5. Να υπολογίσετε το εμβαδόν σφαίρας ακτίνας ρ=10.
6. Να βρείτε τον λόγο των επιφανειών δύο σφαιρών αν ο λόγος των ακτίνων τους είναι λ.
7. Να υπολογίσετε τον όγκο σφαίρας με ακτίνα 3.
8. Να υπολογίσετε τον λόγο των όγκων δύο σφαιρών αν ο λόγος των ακτίνων τους είναι λ.
9. Δίνονται δύο ομόκεντρες σφαίρες με ακτίνες ρ και ρ'. Φέρουμε επίπεδο εφαπτόμενο στη μικρότερη σφαίρα. Να υπολογίσετε το εμβαδόν του κύκλου κατά τον οποίο τέμνεται η μεγάλη σφαίρα από επίπεδο που εφάπτεται στη μικρή.
10. Κυλινδρικός λέβητας έχει ύψος ίσο με την ακτίνα του ρ και καταλήγει σε δύο ημισφαίρια. Να υπολογίσετε το ρ, ώστε ο συνολικός όγκος να είναι 63π.

Αποδεικτικές Ασκήσεις

1. Δίνονται τα στερεά: i) κύλινδρος ακτίνας ρ και ύψους 2ρ, ii) κώνος ακτίνας ρ και ύψους ρ και iii) σφαίρα ακτίνας ρ. Να αποδείξετε ότι (α) ο όγκος της σφαίρας ισούται με τέσσερις όγκους κώνου, (β) δύο όγκοι κυλίνδρου είναι τρεις σφαίρες και (γ) δύο ολικές επιφάνειες του κυλίνδρου ισοδυναμούν με τρεις φορές την επιφάνεια της σφαίρας.

2. Να αποδείξετε ότι αν δύο σφαίρες τέμνονται, η τομή τους είναι κύκλος.

Μικροπείραμα

3. Να αποδείξετε ότι ο όγκος σφαίρας ακτίνας ρ, ο όγκος ισόπλευρου κυλίνδρου περιγεγραμμένου στη σφαίρα (δηλαδή κυλίνδρου με ακτίνα ρ και ύψος 2ρ) και ο όγκος ισοσκελούς κώνου περιγεγραμμένου στη σφαίρα (δηλαδή κώνου περιγεγραμμένου στη σφαίρα που έχει διάμετρο βάσης ίση με ακμή) είναι ανάλογοι των αριθμών 4, 6 και 9 αντίστοιχα.

Μικροπείραμα

Σύνθετα θέματα

1. Να βρείτε το λόγο του ύψους κυλίνδρου προς την ακτίνα σφαίρας αν έχουν ίσες ακτίνες και ισοδύναμες κυρτές επιφάνειες.
2. Σε σφαίρα ακτίνας ρ εγγράφεται κώνος. Να βρείτε την απόσταση της βάσης του κώνου από το κέντρο ώστε ο κώνος να έχει μέγιστο όγκο. Το ίδιο και για κύλινδρο εγγεγραμμένο σε σφαίρα. 3. Να βρείτε το λόγο των εμβαδών και των όγκων σφαίρας και του εγγεγραμμένου σε αυτήν (i) κύβου, (ii) κανονικού οκταέδρου.
4. Σφαίρα, κύλινδρος και κώνος έχουν ίσες ακτίνες και τα ύψη του κώνου και του κυλίνδρου είναι ίσα με την διάμετρο της σφαίρας. Να υπολογίσετε τους λόγους των κυρτών επιφανειών του κυλίνδρου και του κώνου προς την επιφάνεια της σφαίρας. Το ίδιο και για τους όγκους τους.
5. Αν V_α, V_β και V_γ είναι οι όγκοι που παράγονται από ορθογώνιο τρίγωνο αν αυτό περιστραφεί γύρω από τις πλευρές α, β και γ αντίστοιχα, τότε ισχύει:
1V_α² = 1V_β² + 1V_γ² .

Να βρεθεί επίσης ο λόγος V_βV_γ .

Κ Ε Φ Α Λ Α Ι Ο 13. Σ Τ Ε Ρ Ε Α Σ Χ Η Μ Α Τ Α

ΔΡΑΣΤΗΡΙΟΤΗΤΑ

Δίνεται τετραγωνική πυραμίδα Κ.ΑΒΓΔ, με βάση τετράγωνο ΑΒΓΔ πλευράς α, η έδρα ΚΑΔ είναι ισόπλευρο τρίγωνο και οι γωνίες ΚΑΒ και ΚΔΓ είναι ορθές.
i) Να αποδειχθεί ότι η δίεδρη γωνία ΑΔ(Κ,Γ) είναι ορθή.
ii) Από το σημείο Α φέρουμε την ΑΒ' κάθετη στην ακμή ΚΒ και από το Β' επίπεδο παράλληλο στο ΑΒΓΔ που τέμνει τις ακμές ΚΑ, ΚΓ και ΚΔ στα σημεία Α', Γ' και Δ'. Να υπολογισθεί ο όγκος της κόλουρης πυραμίδας ΑΒΓΔ-Α'Β'Γ'Δ'.
iii) Να αποδειχθεί ότι η πυραμίδα Κ.ΑΒΓΔ είναι εγγράψιμη σε σφαίρα και να υπολογισθεί ο όγκος και η επιφάνειά της.

Μικροπείραμα

ΑΝΑΚΕΦΑΛΑΙΩΣΗ

1. Η σχετική θέση σφαίρας (Ο,ρ) και επιπέδου π εξαρτάται από την απόσταση δ του επιπέδου από το κέντρο Ο ως εξής:

δ>ρ, το επίπεδο και η σφαίρα δεν έχουν κοινά σημεία.
δ=ρ, το επίπεδο και η σφαίρα έχουν ένα κοινό σημείο. Το επίπεδο εφάπτεται στη σφαίρα,
δ<ρ, το επίπεδο τέμνει τη σφαίρα σε κύκλο με ακτίνα $\sqrt{ρ^2 - δ^2}$ και κέντρο την προβολή του κέντρου της σφαίρας στο επίπεδο.

2. Η σχετική θέση σφαίρας (Ο,ρ) και ευθείας ε εξαρτάται από την απόσταση δ του κέντρου Ο από την ευθεία ως εξής:

δ>ρ, η ευθεία δεν έχει κοινά σημεία με τη σφαίρα.
δ=ρ, η ευθεία έχει ένα κοινό σημείο με τη σφαίρα, δηλαδή η ευθεία εφάπτεται στη σφαίρα.
δ<ρ, η ευθεία τέμνει τη σφαίρα σε δύο σημεία.

3. Εμβαδόν επιφάνειας σφαίρας (Ο,ρ): Ε=4πρ²

4. Όγκος σφαίρας (Ο,ρ): V = 43 πρ³.

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ

1. Να βρείτε σημείο του οποίου το άθροισμα των τετραγώνων των αποστάσεών του από τις κορυφές ενός τετραέδρου να είναι ελάχιστο.
2. Η τομή τετραέδρου με επίπεδο παράλληλο σε δύο απέναντι ακμές είναι παραλληλόγραμμο.

Μικροπείραμα Μικροπείραμα

3. Δίνονται τρεις ευθείες ε, ζ και ξ ανά δύο ασύμβατες, που δεν είναι παράλληλες στο ίδιο επίπεδο. Να κατασκευάσετε παραλληλεπίπεδο που έχει τρεις ακμές του στις ευθείες αυτές.
4. Το επίπεδο που διχοτομεί μία δίεδρη γωνία ενός τετραέδρου χωρίζει την απέναντι ακμή σε μέρη ανάλογα των προσκείμενων εδρών.

Μικροπείραμα

5. Σε κάθε τετράεδρο οι τρεις ευθείες που συνδέουν τα μέσα των απέναντι ακμών διχοτομούνται. Τα τμήματα αυτά λέγονται διδιάμεσοι και το σημείο αυτό λέγεται κέντρο βάρους του τετραέδρου.

Μικροπείραμα

6. Οι τέσσερις διάμεσοι τετραέδρου, δηλαδή τα τμήματα που συνδέουν τις κορυφές με τα κέντρα βάρους των απέναντι εδρών, διέρχονται από το ίδιο σημείο και τις χωρίζει σε λόγο 1:3.

Μικροπείραμα

7. Να αποδείξετε ότι οι ευθείες που συνδέουν τα μέσα των απέναντι ακμών τετραέδρου (διδιάμεσοι) διέρχονται από το κέντρο βάρους του τετραέδρου.
8. Να βρείτε εσωτερικό σημείο τετραέδρου τέτοιο ώστε τα τετράεδρα που σχηματίζονται με κορυφή το σημείο αυτό και βάσεις τις έδρες του αρχικού τετραέδρου να είναι ισοδύναμα.

Μικροπείραμα

13.19 Κανονικά πολύεδρα

Ένα πολύεδρο λέγεται κανονικό όταν όλες οι έδρες του είναι ίσα κανονικά πολύγωνα και όλες οι πολυεδρικές γωνίες του είναι ίσες.

Από τον ορισμό αυτό προκύπτει ότι όλες οι ακμές ενός κανονικού πολυέδρου είναι ίσα ευθύγραμμα τμήματα, καθώς επίσης και όλες οι επίπεδες γωνίες των εδρών του είναι ίσες. Από τα πολύεδρα που εξετάσαμε έως τώρα, κανονικά ήταν το κανονικό τετράεδρο και ο κύβος. Στην παράγραφο αυτή θα εξετάσουμε όλα τα κανονικά πολύεδρα που μπορούν να κατασκευασθούν.

Όπως αναφέραμε στην § 13.1, για το πλήθος των κορυφών Κ, των ακμών Α και των εδρών Ε ενός πολυέδρου, ισχύει το θεώρημα του Euler:

Ε + Κ = Α + 2 (1).

Κ Ε Φ Α Λ Α Ι Ο 13. Σ Τ Ε Ρ Ε Α Σ Χ Η Μ Α Τ Α

Ένα κανονικό πολύεδρο έχει έδρες που είναι κανονικά πολύγωνα και έστω ν ο αριθμός των πλευρών κάθε έδρας. Οι Ε έδρες έχουν συνολικά νΕ πλευρές, οι οποίες ανά δύο ταυτίζονται για να δώσουν μία ακμή του πολυέδρου, άρα οι ακμές είναι:

$Α = \dfrac{vΕ}{2}$ (2).

Επίσης, κάθε έδρα του κανονικού πολυέδρου έχει ν κορυφές και το σύνολο των επίπεδων γωνιών όλων των εδρών του είναι νΕ. Θεωρούμε ότι αυτές ενώνονται ανά μ για να δώσουν μία στερεά γωνία του κανονικού πολυέδρου, που αντιστοιχεί σε κάθε κορυφή του. Επομένως οι κορυφές είναι

$Κ = \dfrac{vΕ}{μ}$ (3).

Αντικαθιστώντας τα Α και Κ στην (1) από τις (2) και (3), έχουμε

$Ε = \dfrac{4μ}{(2μ + 2ν -μν)}$ (4).

Αναζητούμε λοιπόν φυσικούς αριθμούς μ, ν και Ε που να ικανοποιούν τη σχέση (4), λαμβάνοντας υπόψη ότι ο παρονομαστής πρέπει να είναι θετικός αριθμός και οι έδρες πρέπει να είναι περισσότερες από τρεις. Οι λύσεις που ικανοποιούν όλες αυτές τις συνθήκες είναι οι εξής:

• Για ν=3 το μ παίρνει τις τιμές μ=3, 4, 5 και το Ε=4, 8, 20 αντίστοιχα, δηλαδή με τρίγωνα σχηματίζεται το κανονικό τετράεδρο, οκτάεδρο και εικοσάεδρο.

• Για ν=4 τότε μ=4 και Ε=6, δηλαδή με τετράγωνα σχηματίζεται μόνο ο κύβος.

• Για ν=5 τότε μ=3 και Ε=12, δηλαδή με κανονικά πεντάγωνα σχηματίζεται μόνο το κανονικό δωδεκάεδρο.

Αυτές είναι οι μόνες λύσεις που επιδέχεται η σχέση (4), επομένως υπάρχουν μόνο πέντε κανονικά πολύεδρα, που λέγονται και Πλατωνικά στερεά. Μελετήθηκαν στην Ακαδημία του Πλάτωνα, στη Σχολή του Πυθαγόρα και ο Ευκλείδης ασχολείται με αυτά στο 13ο βιβλίο των Στοιχείων όπου αποδεικνύει ότι αυτά είναι ακριβώς πέντε (βλ. σχετικό ιστορικό σημείωμα). Στο σχ. 50 εικονίζονται τα πέντε κανονικά πολύεδρα και δίπλα το ανάπτυγμά τους. Τα κανονικά πολύεδρα είναι εγγράψιμα και περιγράψιμα σε σφαίρα. Δηλαδή υπάρχει εσωτερικό σημείο Ο, που είναι κέντρο δύο σφαιρών, αυτής που περνάει από όλες τις κορυφές του κανονικού πολυέδρου και αυτής που εφάπτεται όλων των εδρών, στα κέντρα τους.

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

Σχήμα 50

Στον παρακάτω πίνακα παραθέτουμε τα βασικά στοιχεία των κανονικών πολυέδρων. Από τον πίνακα αυτό και το μήκος της ακμής α κατασκευάζονται τα αναπτύγματα των κανονικών πολυέδρων, αφού γνωρίζουμε το σχήμα των εδρών, το πλήθος των εδρών συνολικά και τον αριθμό των εδρών που συνορεύουν σε κάθε κορυφή του πολυέδρου. Από τα αναπτύγματα μπορούν να κατασκευασθούν τα πολύεδρα.

ΣΧΟΛΙΟ
Ο κύβος με το οκτάεδρο και το δωδεκάεδρο με το εικοσάεδρο λέγονται συζυγή κανονικά πολύεδρα, γιατί, όπως παρατηρούμε από τον πίνακα, οι αριθμοί των εδρών και των κορυφών του ενός ισούνται με τους αριθμούς των κορυφών και των εδρών του άλλου, ενώ το πλήθος των ακμών μένει ίδιο. Για πληρότητα λέμε ότι το τετράεδρο είναι συζυγές με τον εαυτό του. Μία εφαρμογή αυτής της παρατήρησης είναι ότι αν με κορυφές τα κέντρα των εδρών ενός κανονικού πολυέδρου κατασκευάσουμε άλλο κανονικό πολύεδρο, αυτό είναι το συζυγές του. Για παράδειγμα, τα κέντρα των εδρών κύβου είναι κορυφές κανονικού οκταέδρου.

Κ Ε Φ Α Λ Α Ι Ο 13. Σ Τ Ε Ρ Ε Α Σ Χ Η Μ Α Τ Α

ΙΣΤΟΡΙΚΟ ΣΗΜΕΙΩΜΑ

Τα κανονικά πολύεδρα

Η ιδέα να διακρίνουμε τα πολύεδρα σε ομάδες που παρουσιάζουν κάποια ιδιάζουσα κανονικότητα ανάγεται στην αρχαία Ελλάδα. Πώς ακριβώς και γιατί έγινε αυτή η ομαδοποίηση δεν είναι ιστορικά γνωστό. Όλα τα ονομαζόμενα (κυρτά) κανονικά πολύεδρα ήταν γνωστά στους αρχαίους Έλληνες γεωμέτρες, και ορισμένα από αυτά (κύβος, τετράεδρο, οκτάεδρο) πρέπει να ήταν γνωστά και στους Αιγυπτίους.

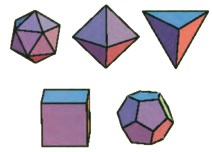
εικόνα

Τα πέντε Πλατωνικά στερεά: εικοσάεδρο, οκτάεδρο, τετράεδρο, κύβος, δωδεκάεδρο

Τα πολύεδρα αυτά συχνά ονομάζονται και Πλατωνικά ή κοσμικά στερεά. Στη φιλοσοφία του Πλάτωνα τα τέσσερα από αυτά συμβολίζουν τέσσερα δομικά στοιχεία του σύμπαντος: το τετράεδρο τη φωτιά, ο κύβος τη γη, το εικοσάεδρο το νερό και το οκτάεδρο τον αέρα. Το πέμπτο, το δωδεκάεδρο, συμβόλιζε τον κόσμο (στα λατινικά ονομαζόταν quinta essentia - «πέμπτη ουσία»). Η θεωρία της κατασκευής των πέντε κανονικών πολυέδρων εκτίθεται στο τέλος των «Στοιχείων», Βιβλίο XIII, του Ευκλείδη, όπου οι ακμές τους εκφράζονται ως συνάρτηση της ακτίνας της περιγεγραμμένης σφαίρας με τη βοήθεια της θεωρίας των αρρήτων του Βιβλίου X και αποδεικνύεται ότι υπάρχουν ακριβώς πέντε κανονικά πολύεδρα. Από αυτά ο κύβος, το τετράεδρο και το δωδεκάεδρο πρέπει να μελετήθηκαν από τους Πυθαγορείους, ενώ η μελέτη του οκταέδρου και του εικοσαέδρου αποδίδεται στο Θεαίτητο. Ο Θεαίτητος ήταν μάλλον ο πρώτος που έγραψε για τα κανονικά στερεά, ενώ σύμφωνα με μια μαρτυρία του Υψικλή, μια δεύτερη πραγματεία πάνω στο θέμα αυτό με τίτλο «Σύγκριση των πέντε κανονικών στερεών» γράφηκε γύρω στο 320 π.Χ. από τον Αρισταίο. Πιθανόν στην πραγματεία αυτή να ανάγονται

οι κατασκευές των εγγεγραμμένων σε σφαίρα κανονικών πολυέδρων που απαντάμε στη «Συναγωγή» του Πάππου. Ο Υψικλής μας μεταφέρει επίσης την μαρτυρία ότι ο Απολλώνιος έγραψε μια συγκριτική μελέτη για το δωδεκάεδρο και το εικοσάεδρο, η οποία όμως δεν διασώθηκε.

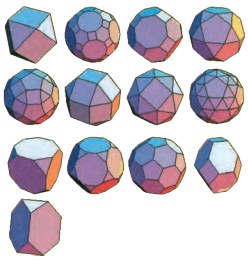
εικόνα

Τα αποκαλούμενα σήμερα Αρχιμήδεια στερεά: κυβοκτάεδρο, (ρομβο)κόλουρο εικοσιδωδεκάεδρο, (ρομβο)κόλουρο κυβοκτάεδρο, κόλουρος κύβος, κόλουρο δωδεκάεδρο, κόλουρο εικοσάεδρο, κόλουρο οκτάεδρο, εικοσιδωδεκάεδρο, ρομβοεικοσιδωδεκάεδρο, ρομβοκυβοκτάεδρο, πεπλατυσμένος κύβος, πεπλατυσμένο δωδεκάεδρο, κόλουρο τετράεδρο.

Σύμφωνα με μαρτυρία του Πάππου, ο Αρχιμήδης στη χαμένη πραγματεία του για τα λεγόμενα ημικανονικά πολύεδρα διακρίνει δεκατρία νέα είδη πολυέδρων, οι έδρες των οποίων είναι κανονικά πολύγωνα, αλλά διάφορων ειδών, και όλες οι κορυφές των οποίων είναι ισοδύναμες, δηλαδή έχουν την ίδια διάταξη εδρών γύρω από κάθε κορυφή. Από αυτά άλλα έχουν δύο είδη πολυγώνων και άλλα τρία. Ο αριθμός των εδρών κυμαίνεται μεταξύ 8 και 92. Σήμερα τα πολύεδρα αυτά ονομάζονται ημικανονικά ή Αρχιμήδεια στερεά.

To ενδιαφέρον στα κανονικά πολύεδρα αναζωογονήθηκε τον 15ο αι. με τις εργασίες του Πιέρο ντελλα Φραντσέσκα (1457) και τη «Θεϊκή αναλογία» του Λουκά Πατσόλι (1509), όπου εξετάζονται Αρχιμήδεια στερεά και τρόποι κατασκευής τους. Στα κανονικά πολύερα αναφέρονται επίσης στο έργο τους ο Φινέος (Orontius Finaeus, 1550) και ο Ράμος (1569).