ΚΕΦΑΛΑΙΟ 4

ΠΑΡΑΛΛΗΛΕΣ ΕΥΘΕΙΕΣ

Στο κεφάλαιο αυτό θα μελετήσουμε τις παράλληλες ευθείες. Αρχικά, με βάση τις γωνίες που σχηματίζουν δύο παράλληλες και μία τέμνουσα θα κατασκευάσουμε από σημείο εκτός ευθείας μία παράλληλη προς αυτή.

Στη συνέχεια, θα δεχθούμε ως αξίωμα το αίτημα παραλληλίας, που είναι ισοδύναμο με το Ευκλείδειο αίτημα και θα μελετήσουμε τις συνέπειές του στα τρίγωνα.

Lazlo Moholy-Nagy, (Ούγκρος, 1895-1946), «Χρώμα -δικτύωμα νο.1» 1922.

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

4.1 Εισαγωγή

Όπως είδαμε στην §2.3, δύο διαφορετικές ευθείες μπορεί να έχουν ένα μόνο κοινό σημείο ή να μην έχουν κανένα κοινό σημείο. Επομένως, οι σχετικές θέσεις δυο ευθειών ε₁ και ε₂, οι οποίες βρίσκονται στο ίδιο επίπεδο, είναι οι παρακάτω:

i) ταυτίζονται (σχ.1α),
ii) τέμνονται (σχ. 1 β),
iii) δεν τέμνονται (σχ.1γ).

Στην τρίτη περίπτωση οι ευθείες ε₁ και ε₂ λέγονται παράλληλες, ώστε:

Δυο ευθείες ε₁ και ε₂ που βρίσκονται στο ίδιο επίπεδο και δεν έχουν κοινό σημείο λέγονται παράλληλες ευθείες.

Για να δηλώσουμε ότι οι ε₁ και ε₂ είναι παράλληλες, γράφουμε ε₁//ε₂.

4.2 Τέμνουσα δυο ευθειών - Ευκλείδειο αίτημα

Ας θεωρήσουμε δύο ευθείες ε₁ και ε₂ του επιπέδου, οι οποίες τέμνονται από τρίτη ευθεία ε₃. Παρατηρούμε ότι σχηματίζονται οκτώ γωνίες.
Οι γωνίες γ, δ, ε, ζ που βρίσκονται μεταξύ των ε₁, ε₂ λέγονται "εντός", ενώ οι γωνίες α, β, η, θ λέγονται "εκτός". Δύο γωνίες που βρίσκονται προς το ίδιο μέρος της τέμνουσας ε₃ λέγονται "επί τα αυτά μέρη", ενώ δύο γωνίες που βρίσκονται εκατέρωθεν της ε₃ λέγονται "εναλλάξ".
Έτσι, με συνδυασμό και των δύο χαρακτηρισμών, οι γωνίες ε και γ λέγονται εντός εναλλάξ, οι γωνίες ε και α λέγονται εντός εκτός και επί τα αυτά μέρη, ενώ οι γωνίες ε και δ λέγονται εντός και επί τα αυτά μέρη.
Χρησιμοποιώντας τις παραπάνω γωνίες, θα αποδείξουμε το επόμενο θεώρημα, που εξασφαλίζει την ύπαρξη παράλληλων ευθειών.

ΘΕΩΡΗΜΑ

Αν δύο ευθείες τεμνόμενες από τρίτη σχηματίζουν δύο εντός εναλλάξ γωνίες ίσες, τότε είναι παράλληλες.

Σχήμα 1

Σχήμα 2

Κ Ε Φ Α Λ Α Ι Ο 4 . Π Α Ρ Α Λ Λ Η Λ Ε Σ Ε Υ Θ Ε Ι Ε Σ

Σχήμα 3

Σχήμα 4

ΑΠΟΔΕΙΞΗ

Έστω ότι ω = φ. Αν οι ευθείες ε₁, ε₂ τέμνονται σε σημείο Γ, η εξωτερική γωνία φ του τριγώνου ΑΒΓ θα είναι ίση με την απέναντι εσωτερική γωνία ω, που είναι άτοπο. (§ 3.10)
Άρα ε₁//ε₂.

ΠΟΡΙΣΜΑ I

Αν δύο ευθείες τεμνόμενες από τρίτη σχηματίζουν δύο εντός, εκτός και επί τα αυτά μέρη γωνίες ίσες ή δύο εντός και επί τα αυτά μέρη παραπληρωματικές, τότε είναι παράλληλες.

ΠΟΡΙΣΜΑ II

Δύο ευθείες κάθετες στην ίδια ευθεία, σε διαφορετικά σημεία της, είναι μεταξύ τους παράλληλες.

ΑΠΟΔΕΙΞΗ

Πράγματι οι γωνίες ω και φ (σχ.4α) είναι ορθές, οπότε ω = φ.
Άρα ε₁//ε₂.

• Θα εξετάσουμε τώρα αν από σημείο εκτός ευθείας μπορούμε να φέρουμε παράλληλες ευθείες προς αυτή και πόσες. Έστω λοιπόν, ευθεία ε και σημείο Α εκτός αυτής (σχ.4β). Φέρουμε την ΑΒ ⊥ ε και ονομάζουμε ε' την ευθεία που είναι κάθετη στην ΑΒ στο σημείο Α. Τότε ε'//ε (αφού και οι δύο είναι κάθετες στην ΑΒ).
Έτσι λοιπόν υπάρχει ευθεία ε' που διέρχεται από ένα σημείο Α που δεν ανήκει στην ε και είναι παράλληλη προς την ευθεία ε. Δεχόμαστε ως αξίωμα ότι η ευθεία αυτή είναι μοναδική, δηλαδή:

Αίτημα παραλληλίας
Από σημείο εκτός ευθείας άγεται μία μόνο παράλληλη προς αυτή.

ΣΧΟΛΙΟ
Το παραπάνω αξίωμα είναι ισοδύναμο με το 5ο αίτημα των
"Στοιχείων" του Ευκλείδη (Ευκλείδειο αίτημα). Το Ευκλείδειο
αίτημα ή κάποιο ισοδύναμο του καθορίζει τη φύση
ολόκληρης της Γεωμετρίας και αποτελεί βάση για τα περισσότερα
θεωρήματα της Ευκλείδειας Γεωμετρίας. (βλ. Ιστορικό σημείωμα,
σελ. 90).

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

Ιδιότητες παράλληλων ευθειών

Άμεσες συνέπειες του αιτήματος παραλληλίας είναι οι παρακάτω προτάσεις.

Πρόταση I

Αν δυο παράλληλες ευθείες τέμνονται από τρίτη, σχηματίζουν τις εντός εναλλάξ γωνίες ίσες.

ΑΠΟΔΕΙΞΗ

Έστω ότι ε₁//ε₂και ε μια τέμνουσα (σχ. 5). Θα αποδείξουμε π.χ. ότι ω = φ. Αν οι γωνίες ω και φ δεν είναι ίσες, φέρουμε την Αx ώστε οι γωνίες xAB και φ να βρίσκονται εκατέρωθεν της ε και να είναι ίσες. Τότε Αx//ε₂ γιατί τεμνόμενες από την ΑΒ σχηματίζουν δύο εντός και εναλλάξ γωνίες ίσες. Κατά συνέπεια υπάρχουν δύο παράλληλες από το Α προς την ε₂, που είναι άτοπο.
Άρα ω = φ.

ΠΟΡΙΣΜΑ

Αν δύο παράλληλες ευθείες τέμνονται από τρίτη σχηματίζουν
i) τις εντός εκτός και επί τα αυτά μέρη γωνίες ίσες,
ii) τις εντός και επί τα αυτά μέρη γωνίες παραπληρωματικές.

Πρόταση II

Αν δυο διαφορετικές ευθείες ε₁ και ε₂ είναι παράλληλες προς μία τρίτη ευθεία ε, τότε είναι και μεταξύ τους παράλληλες, δηλαδή αν ε₁//ε και ε₂//ε, τότε ε₁//ε₂.

ΑΠΟΔΕΙΞΗ

Αν οι ε₁ και ε₂ τέμνονταν σε σημείο Α, θα είχαμε από το Α δύο παράλληλες προς την ε, που είναι άτοπο. Άρα ε₁//ε₂.

Πρόταση III

Αν δυο ευθείες ε₁ και ε₂ είναι παράλληλες και μία τρίτη ευθεία ε τέμνει τη μία από αυτές, τότε η ε θα τέμνει και την άλλη.

ΑΠΟΔΕΙΞΗ

Υποθέτουμε ότι η ε τέμνει την ε₁ στο Α. Αν η ε δεν έτεμνε τηνε₂, θα ήταν ε//ε₂ και έτσι θα είχαμε από το Α δύο παράλληλες προς την ε₂, πράγμα αδύνατο. Άρα η ε τέμνει την ε₂.

Σχήμα 5

Σχήμα 6

Σχήμα 7

Κ Ε Φ Α Λ Α Ι Ο 4 . Π Α Ρ Α Λ Λ Η Λ Ε Σ Ε Υ Θ Ε Ι Ε Σ

Σχήμα 8

ΣΧΟΛΙΟ
Η πρόταση IV αποτελεί
βασικό κριτήριο με το
οποίο εξετάζουμε αν
δύο ευθείες τέμνονται.

Σχήμα 9

ΠΟΡΙΣΜΑ

Αν μια ευθεία είναι κάθετη σε μια από δύο παράλληλεςευθείες, τότε είναι κάθετη και στην άλλη.

Πρόταση IV

Αν δυο ευθείες τεμνόμενες από τρίτη σχηματίζουν τις εντός και επί τα αυτά μέρη γωνίες με άθροισμα μικρότερο από 2 ορθές, τότε οι ευθείες τέμνονται προς το μέρος της τέμνουσας που βρίσκονται οι γωνίες.

ΑΠΟΔΕΙΞΗ

Έστω ότι η ε τέμνει τις ε₁ ,ε₂ στα Α και Β (σχ. 8) αντίστοιχα και ότι φ + ω ≠ 2∟. Τότε οι ε₁ και ε₂ δεν είναι παράλληλες, αφού φ + ω ≠ 2∟ (Πόρισμα σελ. 77). Έστω ότι οι ε₁ και ε₂ τέμνονται σε σημείο Κ, προς το μέρος της τέμνουσας, που δεν περιέχει τις γωνίες ω και φ. Τότε, όμως, η εξωτερική γωνία ω του τριγώνου ΑΚΒ είναι μεγαλύτερη από τη γωνία A₁ δηλαδή ω > A₁= 2∟- φ ή ω + φ > 2∟, που είναι άτοπο. Άρα οι ε₁,ε₂ τέμνονται προς το μέρος της τέμνουσας που βρίσκονται οι γωνίες ω και φ.

Μικροπείραμα

ΠΟΡΙΣΜΑ

Η κατασκευή τριγώνου με δοσμένη μία πλευρά και τις δύο προσκείμενες σε αυτή γωνίες έχει λύση, αν και μόνο αν το άθροισμα των δύο γωνιών είναι μικρότερο των δύο ορθών. (βλέπε §3.18 - Πρόβλημα 2)

4.3 Κατασκευή παράλληλης ευθείας

Είδαμε παραπάνω ότι υπάρχει ευθεία ε', η οποία διέρχεται από ένα σημείο Α και είναι παράλληλη προς γνωστή ευθεία ε. Για την κατασκευή της ε' φέρουμε από το Α ένα πλάγιο τμήμα ΑΒ προς την ε και ονομάζουμε φ την οξεία γωνία που σχηματίζει το ΑΒ με την ε. Μεταφέρουμε τη γωνία φ (§ 2.6) ώστε να έχει κορυφή το Α, η μια πλευρά της να είναι η ΑΒ και η άλλη πλευρά της ΑΓ να βρίσκεται στο ημιεπίπεδο που δεν ανήκει η γωνία φ. Επειδή ΓAΒ = φ έχουμε ΑΓ//ε, αφού τεμνόμενες από την ΑΒ, σχηματίζουν δύο εντός και εναλλάξ γωνίες ίσες. Έτσι η ευθεία ΑΓ είναι η ζητούμενη ευθεία ε'.

Μικροπείραμα

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

4.4 Γωνίες με πλευρές παράλληλες

Ας θεωρήσουμε δύο γωνίες xAy και x'Βy' με Αx//Βx' καιΑy//Βy', δηλαδή δύο γωνίες που έχουν τις πλευρές τους, μία προς μία παράλληλες. Αν προεκτείνουμε τις Βx' και By' θα τέμνουν τις Αx και Αy στα σημεία Γ και Δ αντίστοιχα. Έτσι όλες οι γωνίες του σχήματος 10 λόγω των παραλλήλων θα είναι ίσες με ω ή φ.

Παρατηρούμε ότι:

• Αν και οι δυο γωνίες είναι οξείες (σχ.11), είναι ίσες.
• Αν και οι δυο γωνίες είναι αμβλείες (σχ.12), είναι ίσες.
• Αν η μία γωνία είναι οξεία και η άλλη αμβλεία (σχ.13), είναι παραπληρωματικές.

Συμπεραίνουμε λοιπόν ότι:
Δυο γωνίες που έχουν τις πλευρές τους παράλληλες, μία προς μία, είναι ίσες αν είναι και οι δυο οξείες ή αμβλείες, ενώ είναι παραπληρωματικές αν η μία γωνία είναι οξεία και η άλλη αμβλεία.

Σχήμα 10

Σχήμα 11

Σχήμα 12

Σχήμα 13

ΕΦΑΡΜΟΓΗ

Έστω ε₁και ε₂ δυο παράλληλες που τέμνονται από ευθεία ε.
Να αποδειχθεί ότι
(i) Οι διχοτόμοι δυο εντός εναλλάξ γωνιών είναι παράλληλες.
(ii) Οι διχοτόμοι δυο εντός και επί τα αυτά μέρη γωνιών είναι κάθετες.

Σχήμα 14

Απόδειξη

(i) Έστω Αx, By οι διχοτόμοι των γωνιών ΔAΒ και ΑΒΓ αντίστοιχα.

Τότε ω = ΔAΒ2 και φ = ΑΒΓ2. Αλλά ΔAΒ = ΑΒΓ (ως εντός εναλλάξ).

Από τα παραπάνω προκύπτει ότι ω = φ. Οι ω και φ όμως είναι εντός εναλλάξ γωνίες των ευθειών Αx και By με τέμνουσα την ΑΒ. Άρα Αx//By.
(ii) Αν Αz διχοτόμος της ΜAΒ, τότε Αz ⊥ Αx (ως διχοτόμοι εφεξής και παραπληρωματικών γωνιών). Αφού Αx//By, θα είναι και Az ⊥ By.

Κ Ε Φ Α Λ Α Ι Ο 4 . Π Α Ρ Α Λ Λ Η Λ Ε Σ Ε Υ Θ Ε Ι Ε Σ

Σχήμα 15

4.5 Αξιοσημείωτοι κύκλοι τριγώνου

Στην παράγραφο αυτή χρησιμοποιούμε το Ευκλείδειο αίτημα για να μελετήσουμε τους κύκλους που σχετίζονται με ένα τρίγωνο.

• Ο περιγεγραμμένος κύκλος τριγώνου

Θα αποδείξουμε ότι για κάθε τρίγωνο υπάρχει κύκλος που διέρχεται από τις τρεις κορυφές του. Ο κύκλος αυτός λέγεται περιγεγραμμένος κύκλος του τριγώνου και επιπλέον αποδεικνύεται ότι το κέντρο του είναι ένα σημείο στο οποίο συντρέχουν και οι τρεις μεσοκάθετοι του τριγώνου και λέγεται περίκεντρο.

ΘΕΩΡΗΜΑ

Οι τρεις μεσοκάθετοι ενός τριγώνου διέρχονται από το ίδιο σημείο, το οποίο είναι κέντρο κύκλου που διέρχεται από τις κορυφές του τριγώνου.

ΑΠΟΔΕΙΞΗ

Έστω τρίγωνο ΑΒΓ και Κ, Λ , Μ τα μέσα των πλευρών του ΑΒ, ΒΓ και ΑΓ αντίστοιχα. Οι μεσοκάθετοι Κx και Λy των ΑΒ, ΒΓ θα τέμνονται σε σημείο Ο, αφού τέμνονται οι κάθετες ευθείες τους ΑΒ και ΒΓ. Το Ο ισαπέχει από τις κορυφές Α και Β αφού ανήκει στη μεσοκάθετο της πλευράς ΑΒ, δηλαδή ΟΑ=ΟΒ. Επίσης ΟΒ=ΟΓ, αφού το Ο ανήκει στη μεσοκάθετο της πλευράς ΒΓ. Επομένως ισχύει ότι ΟΑ=ΟΓ, οπότε το Ο θα ανήκει και στη μεσοκάθετο της ΑΓ. Άρα, ο κύκλος (O,OA) θα διέρχεται από τις τρεις κορυφές του τριγώνου ΑΒΓ και είναι ο περιγεγραμμένος κύκλος του τριγώνου.

Μικροπείραμα

• Ο εγγεγραμμένος κύκλος τριγώνου

Ένας άλλος σημαντικός κύκλος βρίσκεται στο εσωτερικό τριγώνου και εφάπτεται και στις τρεις πλευρές του. Θα αποδείξουμε ότι για κάθε τρίγωνο υπάρχει κύκλος με την ιδιότητα αυτή. Ο κύκλος αυτός λέγεται εγγεγραμμένος κύκλος του τριγώνου και το κέντρο του, το οποίο λέγεται έγκεντρο, θα είναι το σημείο τομής των διχοτόμων των γωνιών του τριγώνου.

ΘΕΩΡΗΜΑ

Οι διχοτόμοι των γωνιών ενός τριγώνου διέρχονται από το ίδιο σημείο, το οποίο είναι κέντρο κύκλου που εφάπτεται και στις τρεις πλευρές του τριγώνου.

Μικροπείραμα Μικροπείραμα

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

ΑΠΟΔΕΙΞΗ

Έστω τρίγωνο ΑΒΓ και οι διχοτόμοι ΒΕ και ΓΖ των γωνιών του Β και Γ αντίστοιχα. Οι ΒΕ και ΓΖ τέμνονται σε σημείο I αφού ΕΒΓ + ΖΓΒ = Β2 + Γ2 < Β + Γ < 2∟ (§ 4.2 - Πρόταση IV)
Το Ι ως σημείο της διχοτόμου της θα ισαπέχει από τις πλευρές της ΒΑ και ΒΓ, δηλαδή ΙΛ = ΙΘ. Ανάλογα το Ι θα ισαπέχει από τις πλευρές της Γ, δηλαδή ΙΘ = ΙΝ. Επομένως το Ι ισαπέχει από τις ΑΒ και ΑΓ και θα ανήκει στη διχοτόμο της γωνίας A.
Τελικά, το Ι είναι το σημείο τομής και των τριών διχοτόμων του τριγώνου. Με κέντρο το Ι και ακτίνα την κοινή απόσταση του Ι από τις πλευρές του ΑΒΓ, γράφεται κύκλος που εφάπτεται και στις τρεις πλευρές του τριγώνου.

Σχήμα 16

ΕΦΑΡΜΟΓΗ

Οι παρεγγεγραμμένοι κύκλοι τριγώνου

Η ιδιότητα των εσωτερικών διχοτόμων ενός τριγώνου να διέρχονται από το ίδιο σημείο ισχύει και όταν θεωρήσουμε δύο εξωτερικές και μία εσωτερική διχοτόμο του τριγώνου. Οι τρεις αυτές διχοτόμοι τέμνονται σε σημείο το οποίο είναι κέντρο κύκλου που εφάπτεται στη μία πλευρά του τριγώνου και στις προεκτάσεις των δύο άλλων. Ο κύκλος αυτός λέγεται παρεγγεγραμμένος και το κέντρο του παράκεντρο του τριγώνου. Σε κάθε τρίγωνο υπάρχουν τρία παράκεντρα, τα οποία συμβολίζουμε Ι_α, Ι_β, Ι_γ, και κατά συνέπεια τρεις παρεγγεγραμμένοι κύκλοι (σχ.17α,β).

Οι διχοτόμοι δυο εξωτερικών γωνιών ενός τριγώνου και η ημιευθεία που διχοτομεί την τρίτη γωνία του τριγώνου διέρχονται από το ίδιο σημείο, το οποίο είναι κέντρο κύκλου που εφάπτεται στη μία πλευρά του τριγώνου και στις προεκτάσεις των δυο άλλων.

Απόδειξη

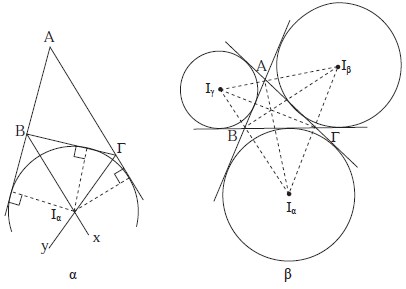Σχήμα 17

Κ Ε Φ Α Λ Α Ι Ο 4 . Π Α Ρ Α Λ Λ Η Λ Ε Σ Ε Υ Θ Ε Ι Ε Σ

Ας θεωρήσουμε τις διχοτόμους Βx και Γy των δύο εξωτερικών γωνιών Β_εξ και Γ_εξ αντίστοιχα, του τριγώνου ΑΒΓ. Οι Βx και Γy τέμνονται σε σημείο I_α, αφού ισχύει ότι:

xΒΓ + yΓΒ = Β_εξ + Γ_εξ2 = 2∟ - Β + Γ2 < 2∟.

Το Ι_α ισαπέχει από τη ΒΓ και την προέκταση της ΑΒ, καθώς και από την προέκταση της ΑΓ. Επομένως ανήκει στη διχοτόμο της γωνίας A, αφού ισαπέχει από τις πλευρές της.

ΑΣΚΗΣΕΙΣ ΓΙΑ ΛΥΣΗ

Ερωτήσεις Κατανόησης

1. i) Πώς ονομάζονται οι γωνίες α και β του παρακάτω σχήματος; Τι σχέση έχουν μεταξύ τους;
ii) Τι ισχύει για τις γωνίες γ και δ;

Εικόνα

2. Να εξηγήσετε γιατί η ΑΒ είναι παράλληλη της ΓΔ.

Εικόνα

3. Αν ω= 120° - θ και φ = 60° + θ να εξηγήσετε γιατί xx'//yy'.

Εικόνα

Μικροπείραμα

4. Να αναφέρετε πέντε (5) τρόπους για να αποδείξουμε ότι δύο ευθείες είναι παράλληλες.
5. Δύο οξείες γωνίες που έχουν τις πλευρές τους παράλληλες είναι:
i) συμπληρωματικές,
ii) ίσες,
iii) παραπληρωματικές,
iv) κανένα από τα παραπάνω.
Να δικαιολογήσετε την απάντησή σας.

Μικροπείραμα

Ασκήσεις Εμπέδωσης

1. Δίνεται ισοσκελές τρίγωνο ΑΒΓ και ευθεία ε παράλληλη προς τη βάση του ΒΓ, που τέμνει τις ΑΒ και ΑΓ στα Δ και Ε αντίστοιχα. Να αποδείξετε ότι το τρίγωνο ΑΔΕ είναι ισοσκελές.
2. Δίνεται γωνία xÔy και σημείο Α της διχοτόμου της. Αν η παράλληλη από το Α προς την Ox τέμνει την Oy στο Β, να αποδείξετε ότι το τρίγωνο ΟΑΒ είναι ισοσκελές.
3. Δίνεται γωνία xÔy και η διχοτόμος της ΟΔ. Από σημείο Α της Oy φέρουμε παράλληλη προς την ΟΔ που τέμνει την προέκταση της Ox στο Β. Να αποδείξετε ότι OA = OB.
4. Δίνεται ισοσκελές τρίγωνο ΑΒΓ (AB = ΑΓ) και σημείο Δ της πλευράς ΑΒ. Αν ο κύκλος (Δ,ΔΒ) τέμνει τη ΒΓ στο Ε, να αποδείξετε ότι ΔΕ//ΑΓ.

Μικροπείραμα

5. Στις προεκτάσεις των πλευρών ΒΑ, ΓΑ τριγώνου ΑΒΓ παίρνουμε αντίστοιχα τα τμήματα: ΑΔ = ΑΒ και ΑΕ=ΑΓ. Να αποδείξετε ότι ΔΕ//ΒΓ.
6. Δίνεται κύκλος (Ο,ρ) και Μ το μέσο χορδής του ΑΒ. Φέρουμε Ox ⊥ OM. Να αποδείξετε ότι Ox//ΑΒ.

Αποδεικτικές Ασκήσεις

1. Δίνεται ισοσκελές τρίγωνο ΑΒΓ (AB = ΑΓ) και η διάμεσος του ΑΜ. Φέρουμε Γx ⊥ ΒΓ προς το ημιεπίπεδο που δεν ανήκει το Α και παίρνουμε σε αυτή τμήμα ΓΔ = ΑΒ. Να αποδείξετε ότι η ΑΔ είναι διχοτόμος της γωνίας ΜAΓ.

Μικροπείραμα
2. Δίνεται τρίγωνο ΑΒΓ και η διχοτόμος του ΑΔ. Από την κορυφή Β φέρουμε ΒΕ//ΑΔ που τέμνει την προ- έκταση της ΓΑ στο Ε. Να αποδείξετε ότι ΕΓ = ΑΒ+ΑΓ.

Μικροπείραμα

3. Δίνεται τρίγωνο ΑΒΓ με ΑΒ < ΑΓ και η εξωτερική διχοτόμος του Αx. Από την κορυφή Β φέρουμε ΒΔ//Αx που τέμνει την ΑΓ στο Δ. Να αποδείξετε ότι ΔΓ = ΑΓ - ΑΒ.
4. Από το έγκεντρο Ι, τριγώνου ΑΒΓ φέρουμε ευθεία παράλληλη της ΒΓ που τέμνει τις ΑΒ και ΑΓ στα σημεία

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

Δ και Ε αντίστοιχα. Να αποδείξετε ότι ΔΕ = ΒΔ+ΓΕ.
5. Από το έγκεντρο I τριγώνου ΑΒΓ φέρουμε ΙΔ//ΑΒ και ΙΕ//ΑΓ. Να αποδείξετε ότι η περίμετρος του τριγώνου ΔΙΕ ισούται με τη ΒΓ.

Σύνθετα θέματα

1. Δίνεται τρίγωνο ΑΒΓ, η διχοτόμος του ΒΔ και η εξωτερική διχοτόμος του Βx. Θεωρούμε δύο σημεία Ε και Κ της πλευράς ΑΒ. Αν ο κύκλος (Ε,ΕΒ) τέμνει τη ΒΔ στο Ζ, ενώ ο κύκλος (Κ,ΚΒ) τέμνει τη Βx στο Μ, να αποδείξετε ότι ΕΖ//ΜΚ.

2. Από τα άκρα ευθύγραμμου τμήματος ΑΒ φέρουμε προς το ίδιο ημιεπίπεδο δύο παράλληλες ημιευθείες Αx και Βγ. Παίρνουμε Γ τυχαίο σημείο του ΑΒ, και στις Αx,Βy τα σημεία Δ και Ε αντίστοιχα, ώστε ΑΔ = ΑΓ και ΒΕ = ΒΓ. Να αποδείξετε ότι η γωνία ΔΓΕ είναι ορθή.

Μικροπείραμα

3. Από το παράκεντρο Ι_α τριγώνου ΑΒΓ με ΑΒ < ΑΓ φέρουμε παράλληλη στην ΑΒ, που τέμνει τις πλευρές ΒΓ και ΑΓ στα σημεία Δ και Ε αντίστοιχα. Να αποδείξετε ότι ΔΕ = ΑΕ - ΒΔ.
4. Δίνεται τρίγωνο ΑΒΓ με ΑΒ<ΑΓ και Μ σημείο της πλευράς ΒΓ. Από το Μ φέρουμε παράλληλη προς τη διχοτόμο ΑΔ της γωνίας A, που τέμνει τις ΑΒ και ΑΓ στα σημεία Ε και Ζ αντίστοιχα. Να αποδείξετε ότι:
i) Το τρίγωνο ΕΑΖ είναι ισοσκελές.
ii) ΒΕ+ΓΖ = σταθερό.
iii) Αν Μ μέσο της ΒΓ τότε:

α) ΒΕ = ΓΖ = ΑΓ + AB2 ,

β) ΑΕ = ΑΖ = ΑΓ - AB2 .

4.6 Άθροισμα γωνιών τριγώνου

Η παραλληλία επιτρέπει να μεταφέρουμε τις γωνίες ενός τριγώνου, ώστε να έχουν κοινή κορυφή μια οποιαδήποτε κορυφή του τριγώνου και να σχηματίζουν ευθεία γωνία(σχ.18). Έτσι μπορούμε να υπολογίσουμε το άθροισμα των γωνιών του τριγώνου.

ΘΕΩΡΗΜΑ

Το άθροισμα των γωνιών κάθε τριγώνου είναι 2 ορθές.

ΑΠΟΔΕΙΞΗ

Από μια κορυφή, π.χ. την Α, φέρουμε ευθεία xy//BΓ. Τότε ω = Β (1) και φ = Γ (2), ως εντός και εναλλάξ των παραλλήλων xy και ΒΓ με τέμνουσες ΑΒ και ΑΓ αντίστοιχα.
Αλλά ω + A + φ = 2∟ (3).
Από τις (1), (2) και (3) προκύπτει ότι

A + Β + Γ = 2∟

Μικροπείραμα

Σχήμα 18

Κ Ε Φ Α Λ Α Ι Ο 4 . Π Α Ρ Α Λ Λ Η Λ Ε Σ Ε Υ Θ Ε Ι Ε Σ

Σχήμα 19

Σχήμα 20

ΠΟΡΙΣΜΑΤΑ

i) Κάθε εξωτερική γωνία τριγώνου είναι ίση με το άθροισμα των δύο απέναντι εσωτερικών γωνιών του τριγώνου.
ii) Αν δύο τρίγωνα έχουν δύο γωνίες ίσες, μία προς μία, έχουν και τις τρίτες γωνίες τους ίσες.
iii) Οι οξείες γωνίες ενός ορθογώνιου τριγώνου είναι συμπληρωματικές.
iv) Κάθε γωνία ισόπλευρου τριγώνου είναι 60^ο.

ΑΠΟΔΕΙΞΗ

Έχουμε A + B + Γ = 2∟ και Γ_εξ + Γ = 2∟, οπότε

A + B + Γ = Γ_εξ + Γ ή

Γ_εξ = A + B.

ii) - iv) Προφανή.

4.7 Γωνίες με πλευρές κάθετες.

ΘΕΩΡΗΜΑ

Δυο οξείες γωνίες που έχουν τις πλευρές τους κάθετες είναι ίσες.

ΑΠΟΔΕΙΞΗ

Έστω οι γωνίες xÔy = ω και x'Ô'y'= φ με Οx⊥O'x' και Oy⊥O'y'.
Τα τρίγωνα ΟΑΓ και Ο'ΒΓ έχουν A = B =1∟ και Γ₁ = Γ₂ (κατακορυφήν).
Άρα θα έχουν και τις άλλες γωνίες ίσες, οπότε ω = φ.

ΠΟΡΙΣΜΑΤΑ

i) Δύο αμβλείες γωνίες που έχουν τις πλευρές τους κάθετες είναι ίσες.
ii) Δύο γωνίες που έχουν τις πλευρές τους κάθετες αλλά η μία είναι οξεία και η άλλη αμβλεία είναι παραπληρωματικές.

ΑΠΟΔΕΙΞΗ

i) Πράγματι, (σχ. 20) είναι θ + ω =2∟, θ' + φ = 2∟, οπότεθ =θ', αφού ω = φ.
ii) Πράγματι, (σχ.20) είναι θ+ ω = 2∟, οπότε θ + φ = 2∟,αφού ω = φ.

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

4.8 Άθροισμα γωνιών κυρτού ν-γώνου

Ας θεωρήσουμε κυρτό πεντάγωνο ΑΒΓΔΕ και Ο τυχαίο εσωτερικό σημείο του. Αν ενώσουμε το Ο με τις κορυφές του πενταγώνου, σχηματίζονται πέντε τρίγωνα. Το άθροισμα των γωνιών κάθε τριγώνου είναι 2 ορθές. Έτσι το άθροισμα των γωνιών και των πέντε τριγώνων είναι (2∙5) ορθές. Αν αφαιρέσουμε το άθροισμα των γωνιών Ô₁+Ô₂+Ô₃+Ô₄+Ô₅ = 4 ορθές, θα μείνει το άθροισμα των γωνιών του πενταγώνου, δηλαδή:

Α + Β + Γ + Δ + Ε = (2∙5 - 4) ορθές.

Όμοια, αν το κυρτό πολύγωνο έχει ν πλευρές και ενώσουμε το Ο με τις κορυφές του σχηματίζονται ν τρίγωνα. Το άθροισμα των γωνιών των ν τριγώνων είναι 2ν ορθές. Αν αφαιρέσουμε το άθροισμα των γωνιών Ô₁+Ô₂+Ô₃+ ... +Ô_ν = 4 ορθές έχουμε:

Α₁ + Α₂ + Α₃ + ... + Α_ν = (2ν - 4) ορθές.

Καταλήξαμε λοιπόν στο συμπέρασμα ότι πρέπει:
Το άθροισμα των γωνιών κυρτού ν-γώνου να είναι 2ν-4 ορθές.

Άλλη απόδειξη. Ας θεωρήσουμε κυρτό πολύγωνο Α₁Α₂... Α_ν με ν πλευρές και ας φέρουμε από μια κορυφή του, π.χ. την Α₁ όλες τις διαγωνίους που διέρχονται από αυτή. Έτσι το πολύγωνο διαιρείται σε ν-2 τρίγωνα, γιατί σε καθεμιά από τις πλευρές του, εκτός των Α₁Α₂ και Α₁Α_ν που διέρχονται από την κορυφή Α₁, αντιστοιχεί ένα τρίγωνο. Επειδή το άθροισμα των γωνιών των ν-2 τριγώνων είναι 2(ν-2)=(2ν-4) ορθές και ισούται με το άθροισμα των γωνιών του πολυγώνου, προκύπτει ότι:
Το άθροισμα των γωνιών κυρτού ν-γώνου είναι 2ν-4 ορθές.

Μικροπείραμα

ΠΟΡΙΣΜΑΤΑ

Το άθροισμα των εξωτερικών γωνιών κυρτού ν-γώνου είναι 4 ορθές.

ΑΠΟΔΕΙΞΗ

Εικόνα

Μικροπείραμα

Σχήμα 21

Σχήμα 22

Σχήμα 23

Σχήμα 24

Κ Ε Φ Α Λ Α Ι Ο 4 . Π Α Ρ Α Λ Λ Η Λ Ε Σ Ε Υ Θ Ε Ι Ε Σ

ΕΦΑΡΜΟΓΗ 1η

Θεωρούμε τρίγωνο ΑΒΓ και τη διχοτόμο Αχ της εξωτερικής γωνίας A του τριγώνου. Να αποδειχθεί ότι το τρίγωνο είναι ισοσκελές, αν και μόνο αν Αx//ΒΓ.

Απόδειξη

(i) Αν β = γ τότε Β = Γ = ω.
Όμως A_εξ = Β + Γ = 2ω, οπότε A_εξ2 = ω ή A₁ = Γ = ω. Άρα Αx//ΒΓ, αφού σχηματίζουν δύο εντός και εναλλάξ γωνίες ίσες.

(ii) Αν Αx//ΒΓ τότε A₁ = Γ (ως εντός εναλλάξ) και A₂ = Β (ως εντός εκτός και επί τα αυτά μέρη). Άρα Β = Γ (αφού A₁ = A₂), οπότε β = γ.

ΕΦΑΡΜΟΓΗ 2η

Σε τρίγωνο ΑΒΓ φέρουμε τις εσωτερικές και εξωτερικές διχοτόμους των γωνιών του Β και Γ. Να αποδειχθεί ότι

(i) Η γωνία των δυο εσωτερικών διχοτόμων είναι ίση με 90° + A2 .

(ii) Η γωνία μίας εσωτερικής και μίας εξωτερικής διχοτόμου είναι ίση με A2.

(iii) Η γωνία των δυο εξωτερικών διχοτόμων είναι ίση με 90° - A2.

Απόδειξη

Οι εσωτερικές διχοτόμοι τέμνονται στο έγκεντρο I. Οι εξωτερικές διχοτόμοι των εξωτερικών γωνιών Β και Γ τέμνονται στο παράκεντρο Ι_α και η εσωτερική διχοτόμος της Β με την εξωτερική διχοτόμο της Γ τέμνονται στο παράκεντρο Ι_β.
(i) Από το τρίγωνο ΒΙΓ παίρνουμε:

ΒΙΓ + Β₁ + Γ₁ = 180° ή ΒΙΓ = 180° - Β₁ - Γ₁ ή

ΒΙΓ = 180° - Β2 - Γ2 ή ΒΙΓ = 90° + 90° - Β2 - Γ2 ή

ΒΙΓ = 90° + A2 (επειδή A2 + Β2 + Γ2 = 90°). (1)

(ii) Η εσωτερική και εξωτερική διχοτόμος μιας γωνίας τέμνονται κάθετα. Έτσι στο τρίγωνο ΙΓΙ_β είναι: Γ = 90° και ΒΙΓ = 90° + Ι_β (2) (ως εξωτερική γωνία).

Από τις (1) και (2) προκύπτει ότι Ι_β = A2. (3)

(iii) Όμοια στο τρίγωνο I_αΒΙ_β είναι Β = 90°, οπότε Ι_α + Ι_β = 90° ή Ι_α = 90° - Ι_β . (4)

Από τις (3) και (4) προκύπτει ότι Ι_α = 90° - A2 .

Μικροπείραμα Μικροπείραμα Μικροπείραμα

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

ΑΣΚΗΣΕΙΣ ΓΙΑ ΛΥΣΗ

Ερωτήσεις Κατανόησης

1. Να υπολογίσετε τη γωνία ω στο παρακάτω σχήμα.

2. Αν AB = ΑΓ και Γx διχοτόμος της ΑΓΔ, να υπολογίσετε τη γωνία φ (βλ. σχήμα).

3. Υπάρχει κυρτό ν-γωνο τέτοιο, ώστε το άθροισμα των εσωτερικών γωνιών του να ισούται με το άθροισμα των εξωτερικών γωνιών του;
4. Να εξηγήσετε γιατί αν ένα ισοσκελές τρίγωνο έχει μια γωνία 60° είναι ισόπλευρο.
5. Το άθροισμα των εξωτερικών γωνιών ενός τριγώνου είναι:
α) 180° β) 270° γ) 360° δ) 540°
ε) κανένα από τα παραπάνω
Να δικαιολογήσετε την απάντησή σας.

Ασκήσεις Εμπέδωσης

1. Σε ορθογώνιο τρίγωνο μια γωνία του είναι ίση με τα 23 μιας άλλης γωνίας του. Να υπολογισθούν όλες οι γωνίες του (δύο περιπτώσεις).
2. Σε ισοσκελές τρίγωνο ΑΒΓ (ΑΒ = ΑΓ) είναι A = Β2. Αν Ι το έγκεντρο του τριγώνου να υπολογισθεί η γωνία ΒΙΓ. (Εφαρμογή 2 - § 4.8).
3. Σε τρίγωνο ΑΒΓ η γωνία A είναι τριπλάσια της γωνίας β. Αν Γ_εξ = 144° να βρεθεί το είδος του τριγώνου ως προς τις πλευρές του.
4. Δίνεται ορθογώνιο τρίγωνο ΑΒΓ (A = 90°) και το ύψος του ΑΔ. Να αποδείξετε ότι Β = ΔAΓ και Γ = ΔAΒ.

5. Στο παρακάτω σχήμα είναι:

ΑΒ = ΑΓ = ΔΒ και xAΓ = 108°.
Να υπολογισθεί η γωνία Δ.

Μικροπείραμα

6. Στο παρακάτω σχήμα είναι: A = 90°, ΑΔ διχοτόμος, ΔΕ//ΑΒ. Αν η γωνία Β είναι 20° μεγαλύτερη από τη Γ να υπολογίσετε τις γωνίες ω και φ.

7. Το άθροισμα των γωνιών κυρτού πολυγώνου είναι900°. Να βρεθεί το πλήθος των πλευρών του.

Αποδεικτικές Ασκήσεις

1. Σε τρίγωνο ΑΒΓ είναι Β_εξ = 90° + A2. Να αποδείξετε ότι ΑΒ = ΑΓ.

Μικροπείραμα Μικροπείραμα

2. Δίνεται τρίγωνο ΑΒΓ με Β > Γ και η διχοτόμος του ΑΔ. Να αποδείξετε ότι
i) ΑΔΓ- ΑΔΒ = Β - Γ,

ii) ΑΔΒ = 90° - Β - Γ2, ΑΔΓ = 90° + Β - Γ2.
3. Σε τρίγωνο ΑΒΓ με Β > Γ φέρουμε το ύψος ΑΔ και τη διχοτόμο ΑΕ. Να αποδείξετε ότι ΔΑΕ = Β - Γ2.

Μικροπείραμα

4. Αν οι διχοτόμοι των γωνιών A, Β κυρτού τετραπλεύρου ΑΒΓΔ τέμνονται σε σημείο Ε, να αποδείξετε ότι ΑΕΒ = Γ + Δ2.

5. Από τυχαίο σημείο Δ της βάσης ΒΓ ισοσκελούς τριγώνου ΑΒΓ φέρουμε τη ΔΕ ⊥ ΑΓ. Να αποδείξετε ότι A = 2ΕΔΓ.
6. Σε ορθογώνιο τρίγωνο ΑΒΓ (A = 90°) το ύψος του ΑΔ και η διχοτόμος του ΒΖ τέμνονται σε σημείο Ε. Να αποδείξετε ότι το τρίγωνο ΑΕΖ είναι ισοσκελές.

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

7. Δίνεται ορθογώνιο τρίγωνο ΑΒΓ (A = 90°). Η διχοτόμος της γωνίας B τέμνει την ΑΓ στο Ζ και την κάθετη στη ΒΓ στο σημείο Γ, στο Η. Να αποδείξετε ότι ΖΓ = ΓΗ.

Σύνθετα Θέματα

1. Δίνεται ισοσκελές τρίγωνο ΑΒΓ (ΑΒ=ΑΓ) και τυχαίο σημείο Δ της πλευράς ΑΒ. Στην προέκταση της ΓΑ προς το Α, παίρνουμε τμήμα ΑΕ = ΑΔ. Να αποδείξετε ότι ΔΕ ⊥ ΒΓ.
2. Δίνεται τρίγωνο ΑΒΓ με Β > Γ και η διχοτόμος του ΑΔ. Από την κορυφή Β φέρουμε ευθεία κάθετη στην ΑΔ, που τέμνει την ΑΓ στο Ε. Να αποδείξετε ότι ΕΒΓ = Β + Γ2.

3. Σε ορθογώνιο τρίγωνο ΑΒΓ προεκτείνουμε την υποτείνουσα ΓΒ κατά τμήμα ΒΔ = ΑΒ. Φέρουμε κάθετη στη ΒΓ στο σημείο Γ και παίρνουμε σε αυτή -προς το μέρος του Α- τμήμα ΓΕ = ΑΓ. Να αποδείξετε ότι τα σημεία Δ, Α, Ε είναι συνευθειακά.
4. Δίνεται ισοσκελές τρίγωνο ΑΒΓ (ΑΒ = ΑΓ) και το ύψος του ΒΔ. Φέρουμε ΔΗ ⊥ ΑΒ, που τέμνει την προέκταση της ΒΓ στο Ε. Να αποδείξετε ότι:
i)ΒΔ = ΔΕ, ii) ΒΓ > ΓΕ.

5. Σε τρίγωνο ΑΒΓ, προεκτείνουμε τα ύψη του ΒΔ και ΓΕ, προς το μέρος των κορυφών και επί των προεκτάσεων παίρνουμε τμήματα ΒΖ=ΑΓ και ΓΗ=ΑΒ αντίστοιχα. Να αποδείξετε ότι
i) ΑΖ=ΑΗ, ii) ΑΖ ⊥ ΑΗ.
6. Θεωρούμε τετράπλευρο ΑΒΓΔ με A > Γ και ονομάζουμε φ την οξεία γωνία των διχοτόμων των γωνιών Β και Δ. Να αποδείξετε ότι φ = Α - Γ2.

7. Δύο επίπεδα κάτοπτρα Κ₁,Κ₂ είναι κάθετα. Φωτεινή ακτίνα α προσπίπτει αρχικά στο Κ₁ και μετά την ανάκλαση στο Κ₂, εξέρχεται κατά την ακτίνα β. Τι πορεία θα ακολουθήσει, σε σχέση με την αρχική ακτίνα α;

Εικόνα

ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ

1. Δίνεται τρίγωνο ΑΒΓ με A = 60° και οι διχοτόμοι του ΒΔ και ΓΕ. Να αποδείξετε ότι ΒΔΓ = ΓEΑ.
2. Θεωρούμε ισόπλευρο τρίγωνο ΑΒΓ (ΑΒ = ΑΓ =ΒΓ= α) και τα σημεία Δ και Ε των πλευρών του ΑΒ και ΒΓ αντίστοιχα, ώστε ΑΔ = ΒΕ = 13α. Να αποδείξετε ότι ΔΕ ⊥ ΒΓ.
3. Δίνεται ορθογώνιο τρίγωνο ΑΒΓ (A = 90°) και η διχοτόμος του ΑΔ. Φέρουμε Δx ⊥ ΒΓ που τέμνει την ΑΒ στο Ε και την προέκτασή της ΑΓ στο Ζ. Να αποδείξετε ότι ΒΕ=ΖΓ.
4. Θεωρούμε τετράπλευρο ΑΒΓΔ με A = Γ = 90° και ΒΓ=ΓΔ. Στην προέκταση της ΑΔ παίρνουμε τμήμα ΔΕ=ΑΒ. Να αποδείξετε ότι ΑΓ ⊥ ΓΕ.
5. Δίνεται τρίγωνο ΑΒΓ με ΑΒ<ΑΓ. Να αποδείξετε ότι:
i) Το ύψος ΑΔ = υ_α σχηματίζει με τη μικρότερη πλευρά μικρότερη γωνία.

ii) Η διάμεσος ΑΜ = μ_α σχηματίζει με τη μικρότερη πλευρά μεγαλύτερη γωνία.
iii) Το ύψος υ_α και η διάμεσος μ_α βρίσκονται εκατέρωθεν της διχοτόμου ΑΕ = δ_α.
6. Τρεις κύκλοι με κέντρα Κ₁,Κ₂,Κ₃ εφάπτονται εξωτερικά στα Α,Β,Γ. Να αποδείξετε ότι ο περιγεγραμμένος κύκλος του τριγώνου ΑΒΓ είναι εγγεγραμμένος στο τρίγωνο Κ₁Κ₂Κ₃.

Μικροπείραμα

7. Θεωρούμε τρίγωνο ΑΒΓ, τον εγγεγραμμένο κύκλο του (Ι,ρ) και τον παρεγγεγραμμένο κύκλο του (I_α, ρ_α). Ονομάζουμε Δ,Ε,Ζ και Δ',Ε',Ζ' τα σημεία επαφής των(Ι, ρ) και (Ι_α, ρ_α) με τις ευθείες ΒΓ,ΓΑ,ΑΒ αντίστοιχα.
Να αποδείξετε ότι:
i) ΑΖ = ΑΕ = τ - α, ΒΔ = ΒΖ = τ - β, ΓΔ = ΓΕ = τ - γ,
ii) ΑΖ' = ΑΕ'= τ,
iii) ΖΖ' = ΕΕ' = α , ΔΔ' = β - γ.

Μικροπείραμα

Κ Ε Φ Α Λ Α Ι Ο 4 . Π Α Ρ Α Λ Λ Η Λ Ε Σ Ε Υ Θ Ε Ι Ε Σ

ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ

1. Να συμπληρώσετε τον πίνακα για κυρτά ν-γωνα..

Εικόνα
i) Τι παρατηρείτε για το άθροισμα των γωνιών κυρτού ν-γώνου; Εξαρτάται από τον αριθμό των πλευρών ν; Τι ισχύει όταν αυξάνεται το ν;
ii) Τι παρατηρείτε για το άθροισμα των εξωτερικών γωνιών κυρτού ν-γώνου. Να σχολιάσετε τη σχέση του με τον αριθμό των πλευρών ν.
2. Να κατασκευάσετε δύο γωνίες με πλευρές παράλληλες (3 περιπτώσεις). Να εξετάσετε τι ισχύει για τις διχοτόμους τους (παράλληλες, κάθετες κτλ.)
Να κάνετε το ίδιο για δύο γωνίες με πλευρές κάθετες.

Εργασία

Να υπολογίσετε τις γωνίες ισοσκελούς τριγώνου ΑΒΓ (ΑΒ=ΑΓ), το οποίο είναι δυνατόν να χωρισθεί σε δύο άλλα ισοσκελή τρίγωνα.
Υπόδειξη: Η ευθεία που χωρίζει το ΑΒΓ σε δυο ισοσκελή τρίγωνα πρέπει να διέρχεται από μια κορυφή του τριγώνου. Να διακρίνετε δύο περιπτώσεις:
i) με ευθεία ΑΔ από την κορυφή Α.
ii) με ευθεία ΒΕ από την κορυφή Β.

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

ΙΣΤΟΡΙΚΟ ΣΗΜΕΙΩΜΑ

Η θεωρία των παραλλήλων

Το αίτημα του Ευκλείδη

Στο Βιβλίο I των «Στοιχείων» του ο Ευκλείδης ορίζει ως παράλληλες «τις ευθείες εκείνες που βρίσκονται στο ίδιο επίπεδο και προεκτεινόμενες επ' άπειρον και

από τα δύο μέρη δε συναντώνται σε κανένα απ' αυτά» (Ορισμός 23). Αμέσως μετά διατυπώνει πέντε αιτήματα, τα τέσσερα πρώτα από τα οποία εκφράζουν τις βασικές ιδιότητες των γεωμετρικών κατασκευών με τη βοήθεια του κανόνα και του διαβήτη, ενώ το πέμπτο αποφαίνεται ότι:
«Εάν μια ευθεία που τέμνει δύο ευθείες σχηματίζει τις εντός και επί τα αυτά μέρη γωνίες μικρότερες από δύο ορθές, τότε οι δύο ευθείες προεκτεινόμενες επ' άπειρον συναντώνται στο μέρος που οι σχηματιζόμενες γωνίες είναι μικρότερες από δύο ορθές» (Αίτημα V).
Το αίτημα αυτό αποδεικνύεται ισοδύναμο με τις εξής προτάσεις:
(Ε1) Υπάρχει ευθεία α και σημείο Α εκτός αυτής τέτοιο, ώστε από το Α διέρχεται μία μοναδική ευθεία που δεν τέμνει την α.
(Ε2) Υπάρχει τετράπλευρο με τέσσερις ορθές γωνίες.
(Ε3) Το άθροισμα των γωνιών τυχόντος τριγώνου ισούται με δύο ορθές.
(Ε4) Υπάρχει τρίγωνο, το άθροισμα των γωνιών του οποίου να ισούται με δύο ορθές.
(Ε5) Αν μια ευθεία τέμνει δύο παράλληλες ευθείες, οι αντίστοιχες γωνίες είναι ίσες.
(Ε6) Τα σημεία που κείνται προς το ίδιο μέρος από δεδομένη ευθεία και σε μία και την αυτή απόσταση, σχηματίζουν ευθεία.
(Ε7) Αν μια ευθεία τέμνει δύο άλλες ευθείες και αυτές αποκλίνουν η μία από την άλλη από το ένα μέρος, τότε από το άλλο μέρος συγκλίνουν.
(Ε8) Υπάρχουν όμοια τρίγωνα.
(Ε9) Υπάρχουν τρίγωνα με οσοδήποτε μεγάλο μέγεθος.
(Ε10)Έστω α τυχούσα ευθεία και Α σημείο εκτός αυτής. Τότε στο επίπεδο που ορίζεται από την ευθεία α και το σημείο Α υπάρχει όχι περισσότερες από μία ευθεία που διέρχεται από το σημείο Α και δεν τέμνει την ευθεία α (Αξίωμα παραλληλίας).
Το αίτημα του Ευκλείδη ή κάποιο ισοδύναμό του καθορίζει τη φύση ολόκληρης της γεωμετρίας και αποτελεί

βάση για τα περισσότερα θεωρήματα της Ευκλείδειας γεωμετρίας.
Η θεωρία των παραλλήλων στην αρχαιότητα και το Βυζάντιο. Είναι πιθανό πριν τη διατύπωση του πέμπτου αιτήματος των «Στοιχείων» του Ευκλείδη να υπήρξαν προσπάθειες να αποδειχθεί. Όμως οι διαθέσιμες μαρτυρίες είναι πενιχρότατες και αποσπασματικές. Ενδείξεις υπάρχουν στα «Αναλυτικά Ύστερα» του Αριστοτέλη, όπου συνδέεται το πρόβλημα των παραλλήλων με την πρόταση (Ε3). Ο Αριστοτέλης ασκεί κριτική στις προσπάθειες μαθηματικών (που δεν κατονομάζονται) να αποδείξουν το Ευκλείδειο αίτημα ότι υποπίπτουν στο λογικό σφάλμα της «λήψης του ζητουμένου» (petitio principi), δηλαδή ότι κατά την απόδειξη χρησιμοποιούν πρόταση ισοδύναμη προς την αποδεικτέα. Άλλη πηγή είναι τα «Σχόλια για τις δυσκολίες στην εισαγωγή του βιβλίου του Ευκλείδη» του Ομάρ Χαγιάμ όπου αναφέρει ότι

«η αιτία του λάθους των ύστερων επιστημόνων στην απόδειξη αυτής της υπόθεσης είναι ότι δε λάμβαναν υπόψη τους τις αρχές του φιλοσόφου [δηλαδή, του Αριστοτέλη]»

και παραθέτει πέντε αρχές, τέσσερις από τις οποίες απαντώνται με λίγο διαφορετική διατύπωση στα «Φυσικά» και το «Περί Ουρανού». Το πρώτο γνωστό έργο της αρχαιότητας, που λίγες μόλις δεκαετίες μετά τα «Στοιχεία» αναφέρεται στη θεωρία των παραλλήλων, είναι η χαμένη πραγματεία του Αρχιμήδη «Περί παραλλήλων», που μνημονεύει ο βιβλιογράφος Ιμπν αλ-Ναντίμ (πέθανε το 993) στο «Βιβλίο της βιβλιογραφίας των επιστημών», μαζί με άλλα έργα του Αρχιμήδη που διασώθηκαν μόνο στα Αραβικά. Το βιβλίο αυτό ήταν πιθανότατα γνωστό στον Θαμπίτ ιμπν Κούρρα (836-901), συγγραφέα δύο πραγματειών σχετικών με τη θεωρία των παραλλήλων. Σύμφωνα με μαρτυρία του Πρόκλου, ο οποίος θεωρεί ότι το αίτημα του Ευκλείδη είναι θεώρημα και επιχειρεί να δώσει μια δική του απόδειξη, ο Ποσειδώνιος είχε προτείνει έναν ορισμό των παραλλήλων, διαφορετικό από αυτόν του Ευκλείδη. Παράλληλες ονομάζει τις ευθείες που βρίσκονται στο ίδιο επίπεδο, δε συγκλίνουν ούτε αποκλίνουν και όλες οι κάθετες από τα σημεία της μιας προς την άλλη είναι ίσες μεταξύ τους. Ο ορισμός αυτός όμως βασίζεται στο ισοδύναμο αξίωμα (Ε6). Ο Πρόκλος αναφέρεται επίσης εκτεταμένα στις προσπάθειες του Κλαύδιου Πτολεμαίου και άλλων μαθηματικών, τους οποίους δεν κατονομάζει, να αποδείξουν το Ευκλείδειο αίτημα.

Κ Ε Φ Α Λ Α Ι Ο 4 . Π Α Ρ Α Λ Λ Η Λ Ε Σ Ε Υ Θ Ε Ι Ε Σ

ΙΣΤΟΡΙΚΟ ΣΗΜΕΙΩΜΑ

Με την απόδειξη του Ευκλείδειου αιτήματος ασχολήθηκε ο Διόδωρος (1ος αι. π.Χ.). Στα Αραβικά διατηρήθηκαν και οι προσπάθειες κάποιου Αγάνη και του Σιμπλίκιου που στηρίζονται στον ορισμό του Ποσειδωνίου και, επομένως, στο αξίωμα (Ε6).
Η θεωρία των παραλλήλων στα Αραβικά μαθηματικά. Η πρώτη γνωστή προσπάθεια απόδειξης του Ευκλείδειου αιτήματος στα Αραβικά μαθηματικά έγινε από τον αλ-Τζαουχαρί στο έργο του «Τελειοποίηση του βιβλίου των "Στοιχείων"», το περιεχόμενο του οποίου μεταφέρει ο Νασίρ αντ-Ντιν αλ-Τουσί. Όμως στην απόδειξή του χρησιμοποιεί την ισοδύναμη προς το αποδεικτέο πρόταση ότι «αν μία ευθεία τέμνει δύο άλλες ευθείες έτσι ώστε οι εντός εναλλάξ γωνίες να είναι ίσες, τότε το ίδιο ισχύει όταν οι δύο ευθείες τέμνονται από οποιαδήποτε άλλη ευθεία». Οι πρώτες προσπάθειες αντικατάστασης του Ευκλείδειου αιτήματος με το αξίωμα της ύπαρξης «ισαπεχόντων» ευθειών ανάγονται στον αλ-Ναιριζί και τον Ιμπν Σίνα (Αβικέννα).
Οι άραβες μαθηματικοί ανέπτυξαν δύο κυρίως προσεγγίσεις στην απόδειξη του Ευκλείδειου αιτήματος, που εγκαινιάζονται στο έργο του Θαμπίτ ιμπν Κούρρα (908-946): τη γεωμετρική και την κινηματική προσέγγιση. Η κινηματική προσέγγιση ακολουθεί το πνεύμα του Αρχιμήδη και αναπτύχθηκε από τον Ιμπν αλ-Χαιθάμ. Η πρωτοτυπία της μεθόδου του αλ-Χαιθάμ, την οποία ακολούθησαν συχνά οι γεωμέτρες στη συνέχεια, είναι ότι υποθέτει την ύπαρξη ενός τετραπλεύρου με τρεις ορθές γωνίες και εξετάζει τις περιπτώσεις η τέταρτη γωνία να είναι οξεία ή αμβλεία, προσπαθώντας να καταλήξει σε αντίφαση με τον ορισμό των παραλλήλων ως «ισαπεχόντων» ευθειών. Η γεωμετρική προσέγγιση αναπτύχθηκε κυρίως από τον Ομαρ Χαγιάμ. Ξεκινώντας από την απόδειξη της πρότασης (Ε2) και με συλλογισμούς συγγενείς με αυτούς του Πρόκλου, αποδεικνύει το Ευκλείδειο αίτημα χωρίς να υποπέσει στο λογικό σφάλμα της «λήψης του ζητουμένου». Ο εγκυκλοπαιδιστής φιλόσοφος, μαθηματικός και αστρονόμος Νασίρ αντ-Ντιν αλ-Τουσί (1201-1274) στη δική του πρωτότυπη απόδειξη του αξιώματος των παραλλήλων ακολουθεί το ύφος του Ιμπν Κούρρα και του Ιμπν αλ-Χαιθάμ, αλλά στηρίζεται σε αξίωμα που αποτελεί ισχυρότερη μορφή του αιτήματος παραλληλίας.
Στη διάρκεια του 13ου αι. συνεχίζονται οι αναζητήσεις απόδειξης του Ευκλείδειου αιτήματος. Ο αλ-Χαναφί, ακολουθώντας παλαιότερες τάσεις που εκδηλώνονται στο έργο του αλ-Κιντί, του αλ-Μπιρουνί (973-περ. 1050) και του Ομάρ Χαγιάμ, συνδέουν το πρόβλημα του Ευκλείδειου αιτήματος με την έννοια της επ' άπειρον

διαιρετότητας των γεωμετρικών μεγεθών. Ιδιαίτερα διαδεδομένη ήταν η θεωρία των παραλλήλων του αλ-Αμπχαρί (ή αλ-Αμπαχρί, πέθανε το1263). Συγγενής προς αυτήν ήταν η θεωρία του αλ-Μαγκριμπί. Στις δύο τελευταίες θεωρίες βρίσκει κανείς ίχνη του ύφους των συλλογισμών του Σιμπλίκιου. Στα τέλη του 13ου-αρχές 14ου αι. μια ακόμα αξιοσημείωτη προσπάθεια γίνεται από τον αντ-Ντιν ασ-Σιραζί (1236-1311), μαθητή του αλ-Τουσί. Παρ' όλες τις προσπάθειες που σκιαγραφήσαμε οι Άραβες μαθηματικοί ήταν πολύ μακριά από την ιδέα ότι είναι δυνατή μια άλλη γεωμετρία. Απλώς προσπαθούσαν να αποδείξουν το Ευκλείδειο αίτημα από υποθέσεις που θεωρούσαν πιο προφανείς. Στην πορεία των προσπαθειών τους απέδειξαν την ισοδυναμία του Ευκλείδειου αιτήματος με διάφορες προτάσεις που μπορούν να θεωρηθούν ισοδύναμες με το πέμπτο αίτημα, καθώς και πολλά θεωρήματα που σήμερα εμπίπτουν στο πεδίο της Υπερβολικής και της Ελλειπτικής Γεωμετρίας.
Η θεωρία των παραλλήλων στην Ευρώπη από τον13ο ως το 18ο αι. Η πρώτη γνωστή απόπειρα απόδειξης του Ευκλείδειου αιτήματος στη μεσαιωνική Ευρώπη απαντάται το 13ο αι. στο σύγγραμμα του Βιτέλο (Vitelo, περίπου 1225-1280) «Οπτική» ή «Προοπτική» (1572). Βασική πηγή του Βιτέλο είναι το έργο του Ιμπν αλ-Χαιθάμ. Ωστόσο, η απόδειξή του υστερεί ως προς το επίπεδο αυστηρότητας που είχαν φτάσει οι Άραβες μαθηματικοί.
Δύο άλλες απόπειρες απαντώνται το 14ο αι. στα «Σχόλια» του Γερσωνίδη (Levi ben Gerson ή Gersonides, 1288-1344) και στο έργο κάποιου Αλφόνσο, ο οποίος εικάζεται ότι είναι ο Ισπανός ιατρός και συγγραφέας πολεμικών θρησκευτικών έργων Αλφόνσο του Βαλλαντολίντ (1270-1346).
Στις αρχές του 16ου αι. η θεωρία παραλλήλων εξετάζεται στο «Κάτοπτρο αστρονομικό που περικλείει την ανθρώπινη σοφία σε κάθε επιστήμη» του Φ.Μπ. Γκρισογκόνο (1472-1538), που εκδίδεται στη Βενετία το 1507. Το 1574 εμφανίζεται μία πρωτότυπη απόδειξη του πέμπτου αιτήματος από τον Κλάβιο (Clavius (Schlussel), 1537-1612) που εργαζόταν στη Ρώμη και συμμετείχε στην επεξεργασία του Γρηγοριανού ημερολογίου. Η απόδειξη του Κλάβιου στηρίζεται στην πρόταση (Ε6). Η απόδειξή του παρουσιάζει ομοιότητες με αυτές του Ιμπν Κούρρα και του Ιμπν αλ-Χαιθάμ, τις οποίες ίσως γνώριζε από δεύτερο χέρι.
Τον 17ο αι. παρατηρείται κάποια ένταση των προσπαθειών στη θεωρία των παραλλήλων, η οποίόμως δεν απέφερε ιδιαίτερα αξιόλογους καρπούς. Δημοσιεύονται το 1603 στην Μπολόνια δύο τομίδια

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

ΙΣΤΟΡΙΚΟ ΣΗΜΕΙΩΜΑ

του Πιέτρο Α. Κατάλντι (1548-1626), το 1658 στην Πίζα η επεξεργασμένη από τον Τζ.Α. Μπορέλλι(1608-1679) έκδοση των «Στοιχείων» του Ευκλείδη, και το 1680 ανάλογη έκδοση των «Στοιχείων» από τον Βιτάλε Τζορντάνο (1633-1711). Το 1693 δημοσιεύεται η πραγματεία του Τζ. Ουώλλις (J. Wallis, 1616-1703) «Το πέμπτο αίτημα και ο πέμπτος ορισμός του Βιβλίου νΙ του Ευκλείδη», το δεύτερο μέρος της οποίας περιέχει μετάφραση μιας απόδειξης που αποδίδεται στον αλ-Τουσί, και στο τρίτο εκτίθεται απόδειξη του Ουώλλις, που βασίζεται στην πρόταση (Ε9), την οποία θεωρεί φυσική «Κοινή Έννοια».
Από την πραγματεία του Ουώλλις γνωρίστηκε με την αποδιδόμενη στον αλ-Τουσί απόδειξη του πέμπτου αιτήματος ο Τζιρόλαμο Σακκέρι (G.G. Saccheri,1667-1733). Ο Σακκέρι ξεκινώντας από το ισόπλευρο τετράπλευρο με τις δύο ορθές του Ομάρ Χαγιάμ και του αλ-Τουσί αναλύει τις ίδιες τρεις υποθέσεις για τις άλλες δύο γωνίες. Αποκλείει την υπόθεση της οξείας γωνίας επειδή θεωρεί ότι στην περίπτωση αυτή, όπως και στην περίπτωση της ορθής γωνίας ισχύει το πέμπτο αίτημα, δηλαδή επειδή αντιφάσκει στα αξιώματα της συνήθους γεωμετρίας του Ευκλείδη. Στην περίπτωση της αμβλείας γωνίας ο Σακκέρι προχωρεί όσο κανείς άλλος πριν από αυτόν στην απόδειξη θεωρημάτων της σημερινής Υπερβολικής Γεωμετρίας. Όμως διολισθαίνοντας σε λάθος συλλογισμό κατέληξε σε αντίφαση, οπότε συμπέρανε ότι η περίπτωση της ορθής γωνίας (δηλαδή της Ευκλείδειας γεωμετρίας) είναι η μόνη δυνατή.
Πιο σημαντική είναι η προσπάθεια του Γερμανού μαθηματικού Λάμπερτ (J.H. Lambert, 1728-1777). Ξεκινώντας από το ίδιο τετράπλευρο του Ομάρ

Χαγιάμ και του Σακκέρι αποκλείει χωρίς δυσκολία την υπόθεση της οξείας γωνίας, στη βάση ότι στην περίπτωση αυτή δύο κάθετες στην ίδια ευθεία τέμνονται, πράγμα που, κατά τη γνώμη του, δεν αντιφάσκει στο πέμπτο αίτημα, αλλά στα υπόλοιπα αξιώματα της Γεωμετρίας του Ευκλείδη. Επίσης παρατηρεί ότι η υπόθεση της οξείας γωνίας ισχύει στην επιφάνεια της σφαίρας αν ως ευθείες ληφθούν οι μέγιστοι κύκλοι της σφαίρας. Εξετάζοντας την υπόθεση της αμβλείας γωνίας ο Λάμπερτ αποδεικνύει ακόμα περισσότερα και από τον Σακκέρι θεωρήματα της σημερινής Υπερβολικής Γεωμετρίας. Προσπαθώντας να λάβει κάποια παράδοξα αποτελέσματα παραδέχεται ότι δεν είναι εύκολο να αποκλεισθεί η υπόθεση της αμβλείας γωνίας. Αντίθετα με τον Σακκέρι, ούτε υποπίπτει σε σφάλμα, ούτε συμπεραίνει ότι η υπόθεση της αμβλείας γωνίας οδηγεί σε αντίφαση. Αντίθετα, εκφράζοντας κάποια έκπληξη για τις «περίεργες» ιδιότητες των σχημάτων στην περίπτωση αυτή (π.χ. ότι χάνεται η έννοια της ομοιότητας και της αναλογίας των σχημάτων, ότι το άθροισμα των γωνιών ενός τριγώνου αυξάνει όσο μειώνεται η επιφάνεια του τριγώνου, κ.α.) διατυπώνει την ιδιαίτερα βαθιά και διορατική σκέψη ότι «η τρίτη υπόθεση ισχύει σε κάποια φανταστική σφαίρα».
Από τις προσπάθειες μετά τον Λάμπερτ, αξίζει να αναφερθεί η «απόδειξη» του Λ. Μπερτράν (L. Bertrand, 1731-1812), μαθητή του Όυλερ, το 1778, του Α.Μ. Λεζάντρ (1752-1833), που αφιέρωσε σαράντα χρόνια στις έρευνες στη θεωρία των παραλλήλων, του Σ.Ε. Γκούριεφ (1764-1813), και του Φαρκάς Μπόλυαι (Farkas Bolyai, 1775-1856), του πατέρα του Γιάνος Μπόλυαι, του μετέπειτα δημιουργού της μη Ευκλείδειας Γεωμετρίας.

Κ Ε Φ Α Λ Α Ι Ο 4 . Π Α Ρ Α Λ Λ Η Λ Ε Σ Ε Υ Θ Ε Ι Ε Σ

ΑΝΑΚΕΦΑΛΑΙΩΣΗ

Δύο ευθείες ενός επιπέδου		• ταυτίζονται όταν έχουν 2 κοινά σημεία. • τέμνονται όταν έχουν 1 κοινό σημείο. • είναι παράλληλες όταν δεν έχουν κοινό σημείο.

Από σημείο Α εκτός ευθείας ε		• υπάρχει ευθεία εʹ//ε. • δεχόμαστε αξιωματικά ότι η εʹ είναι μοναδική. (Αίτημα παραλληλίας)

Δύο ευθείες ε₁ και ε₂ είναι παράλληλες αν:


Έστω ε₁//ε₂ και ε μια τρίτη ευθεία.


Δύο γωνίες που έχουν παράλληλες ή κάθετες πλευρές είναι:

Ε Υ Κ Λ Ε Ι Δ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α

Αξιοσημείωτοι κύκλοι τριγώνου και κέντρα τους

Το άθροισμα των εσωτερικών γωνιών