5-6 Η ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ ΠΟΛΛΩΝ
ΣΗΜΕΙΑΚΩΝ ΦΟΡΤΙΩΝ Έστω ένα σύστημα που αποτελείται από τρία σημειακά φορτία, τα q1, q2 και q3 (Σχ. 5.19). Ας ονομάσουμε τις θέσεις τους Α, Β, Γ και τις μεταξύ τους αποστάσεις α, β και γ, όπως στο σχήμα 3.19. Η ενέργεια που έχει η ομάδα των τριών φορτίων είναι ίση με το έργο που απαιτείται για να μεταφερθούν αυτά τα φορτία από πολύ μακριά και να τοποθετηθούν στις θέσεις τους. Ας συγκεντρώσουμε τα φορτία μεταφέροντάς τα ένα - ένα.
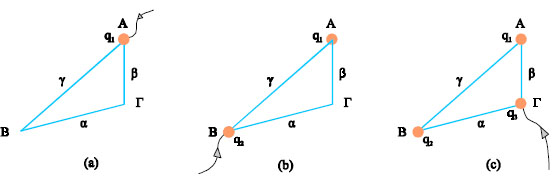 Σχ. 5.20 Αρχικά τοποθετούμε το q1 στο σημείο Α(a), στη συνέχεια το q2 στο σημείο Β(b) και τέλος το q3 στο Γ(c). Σχ. 5.20 Αρχικά τοποθετούμε το q1 στο σημείο Α(a), στη συνέχεια το q2 στο σημείο Β(b) και τέλος το q3 στο Γ(c).
Το φορτίο q1 μπορεί να μεταφερθεί στο σημείο Α χωρίς παραγωγή ή δαπάνη έργου. Στη συνέχεια, μεταφέρουμε το q2 στο σημείο Β. Το φορτίο q2, κινείται μέσα στο πεδίο που έχει δημιουργηθεί από το q1. Το έργο που απαιτείται για να μεταφερθεί το φορτίο είναι αντίθετο του έργου της δύναμης του πεδίου.
Ας μεταφέρουμε τώρα το q3. Το έργο της δύναμης που απαιτείται για την μεταφορά του είναι αντίθετο του έργου της δύναμης του πεδίου που δημιουργούν τα q1 και q2 μαζί.
Επειδή το δυναμικό στο σημείο Γ οφείλεται στα φορτία q1 και q2 και είναι
|
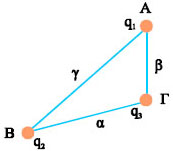 Σχ. 5.19 Σύστημα τριών σημειακών φορτίων. Σχ. 5.19 Σύστημα τριών σημειακών φορτίων.
|
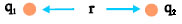 Σχ. 5.21 Το σύστημα δύο σημειακών φορτίων που απέχουν μεταξύ τους απόσταση r έχει δυναμική ενέργεια. Σχ. 5.21 Το σύστημα δύο σημειακών φορτίων που απέχουν μεταξύ τους απόσταση r έχει δυναμική ενέργεια. |
η σχέση (5.22) γίνεται
Το συνολικό έργο, που απαιτείται για να συγκεντρώσουμε τα τρία φορτία, προκύπτει από το άθροισμα των σχέσεων (5.21) και (5.23) και είναι
Τόση είναι και η δυναμική ενέργεια του συστήματος
Να σημειώσουμε ότι η δυναμική ενέργεια που υπολογίσαμε ανήκει στο σύστημα των φορτίων. Δεν υπάρχει κανένας λογικός τρόπος να αποδώσουμε μέρος αυτής της ενέργειας σε κάποιο από τα φορτία.
Στην περίπτωση δύο σημειακών φορτίων q1 και q2 που απέχουν απόσταση r η δυναμική ενέργεια του συστήματος είναι
Από τη σχέση (5.26) προκύπτει ότι αν τα φορτία είναι ομώνυμα η δυναμική τους ενέργεια είναι θετική. Αυτό είναι συνέπεια των απωστικών δυνάμεων που αναπτύσσονται μεταξύ τους. Για να μεταφερθούν τα φορτία από πολύ μακριά και να πλησιάσουν σε απόσταση r πρέπει να προσφερθεί έργο στο σύστημα. Αντίθετα, αν τα φορτία είναι ετερώνυμα έλκονται και απαιτείται αρνητικό έργο για να τοποθετηθούν σε απόσταση r μεταξύ τους. Επομένως η δυναμική τους ενέργεια είναι αρνητική.
|
ΠΑΡΑΔΕΙΓΜΑ 5-6
Σφαιρίδιο μάζας m1= 22 x 10-5kg φορτισμένο με θετικό φορτίο q1= 11 x 10-7C βάλλεται με αρχική ταχύτητα υo= 30 m/s προς δεύτερο σφαιρίδιο με μάζα m2= 2m1 και φορτίο q2= 2q1 που είναι αρχικά ακίνητο σε απόσταση d = 2m από το πρώτο. Αν τα σφαιρίδια βρίσκονται πάνω σε οριζόντιο, λείο και μονωτικό δάπεδο να βρεθεί η ελάχιστη απόσταση L στην οποία θα πλησιάσουν. Δίνεται Κc = 9 x 109 Ν m2 /C2.
Απάντηση:
Η μηχανική ενέργεια του συστήματος διατηρείται. Αν θεωρήσουμε ως αρχική θέση τη θέση από την οποία βάλλεται το σφαιρίδιο m1 και ως τελική τη θέση που τα σφαιρίδια βρίσκονται στην ελάχιστη απόσταση μεταξύ τους θα ισχύει
Επειδή στο σύστημα δεν ασκούνται εξωτερικές δυνάμεις, η ορμή του συστήματος διατηρείται.
Θεωρώντας θετική κατεύθυνση την αρχική φορά κίνησης του m1 η παραπάνω σχέση γράφεται αλγεβρικά
αντικαθιστώντας στην (5.27) και λύνοντας ως προς L προκύπτει
Παρατήρηση: Για τη λύση του προβλήματος χρησιμοποιήσαμε την αρχή διατήρησης της μηχανικής ενέργειας. Όμως, το πεδίο που δημιουργείται από κινούμενα φορτία είναι ηλεκτρομαγνητικό πεδίο και όταν, όπως συμβαίνει στο πρόβλημά μας τα φορτία επιταχύνονται ένα μέρος της ενέργειάς τους μεταφέρεται με τη μορφή ηλεκτρομαγνητικής ακτινοβολίας στο περιβάλλον |