Φυσική (Β Λυκείου Θετικών Σπουδών) - Βιβλίο Μαθητή (Εμπλουτισμένο)
| TO ΠΕΙΡΑΜΑ TOY MILLIKAN Την περίοδο 1909-1913, o Robert Millikan (Μίλικαν), με ένα εμπνευσμένα απλό πείραμα που πραγματοποίησε στο πανεπιστήμιο του Σικάγου, μέτρησε για πρώτη φορά το στοιχειώδες φορτίο e και απέδειξε ότι το ηλεκτρικό φορτίο είναι κβαντισμένο -υπάρχει δηλαδή μόνο σε διακριτές ποσότητες, που είναι ακέραια πολλαπλάσια του στοιχειώδους φορτίου e.
Στο σχήμα βλέπουμε το μοντέλο της πειραματικής συσκευής του Millikan. Αποτελείται από δύο παράλληλες μεταλλικές πλάκες. Η πάνω πλάκα έχει μια μικρή τρύπα από την οποία διέρχονται μικρά σταγονίδια λαδιού. Τα σταγονίδια αυτά είναι φορτισμένα λόγω της τριβής τους με το ακροφύσιο του ψεκαστήρα με το οποίο ψεκάζεται το λάδι. Μια οριζόντια δέσμη φωτός φωτίζει τα σταγονίδια λαδιού, τα οποία μπορούν να παρατηρηθούν με ένα μικροσκόπιο. Καθώς το φως πέφτει πάνω στα σταγονίδια αυτά φαίνονται σαν λαμπερά σημεία μέσα στο σκοτάδι.
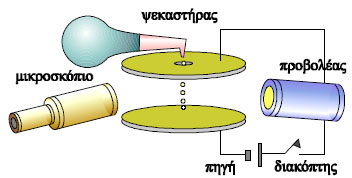 Σχ. 5.61 Το μοντέλο της συσκευής του Millikan
Έστω ένα σταγονίδιο μάζας m που είναι φορτισμένο με αρνητικό φορτίο q, λόγω της τριβής του με το ακροφύσιο του ψεκαστήρα. Εάν δεν υπάρχει ηλεκτρικό πεδίο ανάμεσα στις πλάκες, στο σταγονίδιο δρουν δυο δυνάμεις: το βάρος του mg που κατευθύνεται προς τα κάτω, και η αντίσταση του αέρα F, που κατευθύνεται προς τα πάνω.
Η αντίσταση (F) δεν είναι σταθερή αλλά εξαρτάται από την ταχύτητα με την οποία πέφτει το σταγονίδιο. Για μικρές ταχύτητες, η αντίσταση που δέχεται στον αέρα μια μικρή σφαίρα, όπως οι σταγόνες του λαδιού, δίνεται από τη σχέση
όπου μ το ιξώδες του αέρα (ιξώδες: ένα μέγεθος που δείχνει πόσο παχύρρευστο είναι ένα ρευστό), r η ακτίνα της σταγόνας και υ η ταχύτητά της.
Όσο το βάρος mg είναι μεγαλύτερο από την αντίσταση, η σταγόνα επιταχύνεται. Καθώς όμως η ταχύτητά της αυξάνεται, μεγαλώνει η αντίσταση και σύντομα γίνεται αντίθετη με το βάρος. Τότε η σταγόνα αποκτά μια τελική, οριακή ταχύτητα.
|
| Η μάζα της σταγόνας μπορεί να γραφεί, όπου η πυκνότητα και ο όγκος της σταγόνας. Ο
Οπότε η σχέση (5.65) γίνεται
Η ταχύτητα με την οποία κινείται ένα σταγονίδιο είναι μερικά εκατοστά του εκατοστού του μέτρου το δευτερόλεπτο και επομένως είναι δυνατόν να μετρηθεί, οπότε η σχέση (5.66) μας δίνει την ακτίνα της σταγόνας. Έστω τώρα ότι συνδέουμε τις δύο πλάκες με τους πόλους μιας πηγής, έτσι ώστε η επάνω πλάκα να έχει το υψηλό δυναμικό. Τώρα εκτός από τις δύο δυνάμεις που αναφέρθηκαν προηγουμένως, στο σταγονίδιο ασκείται και μια δύναμη από το πεδίο Εq. Υποθέσαμε ότι το φορτίο q είναι αρνητικό, επομένως η ηλεκτρική δύναμη κατευθύνεται προς τα πάνω. Από το μέτρο της δύναμης θα εξαρτηθεί αν το σταγονίδιο θα συνεχίσει να κινείται προς τα κάτω, με μικρότερη ταχύτητα, ή θα αντιστρέψει την κίνησή του. Όπως και να ‘χει η συνισταμένη των τριών δυνάμεων γίνεται πάλι μηδέν και τότε η σταγόνα τελικά αποκτά μια νέα οριακή ταχύτητα. Ας πάρουμε την περίπτωση όπου η ηλεκτρική δύναμη είναι αρκετά μεγάλη και το σταγονίδιο κινείται προς τα πάνω, τότε η αντίσταση F, κατευθύνεται προς τα κάτω. Αν υ΄ είναι η νέα οριακή ταχύτητα που θα αποκτήσει η σταγόνα, ισχύει
Μετρώντας την υ΄ και έχοντας ήδη υπολογίσει την ακτίνα, από την σχέση (5.66) μπορούμε να υπολογίσουμε το φορτίο q. Με μια μεγάλη σειρά μετρήσεων ο Millikan βρήκε ότι το φορτίο κάθε σταγόνας ήταν ακέραιο πολλαπλάσιο μιας στοιχειώδους ποσότητας φορτίου e. Έκανε ακόμα την υπόθεση ότι, το φορτίο αυτό ήταν ίσο, σε απόλυτη τιμή, με το φορτίο ενός ηλεκτρονίου. Η υπόθεσή του επιβεβαιώθηκε. Για την εργασία του αυτή ο Millikan τιμήθηκε το 1923 με το βραβείο Νόμπελ. |
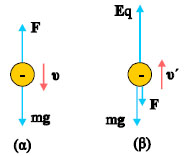 Σχ. 5.62 (α) Οι δυνάμεις στην σταγόνα που πέφτει με την οριακή της ταχύτητα υ. (β) Οι δυνάμεις παρουσία του ηλεκτρικού πεδίου. |
