|
| Ηλεκτρική ροή - νόμος του Gauss |
| |
|
| 43 |
Ένας δίσκος ακτίνας r = 0,2m βρίσκεται μέσα σε ομογενές ηλεκτρικό πεδίο έντασης Ε=500Ν/C. Υπολογίστε την ηλεκτρική ροή που διέρχεται από το δίσκο, αν: |
| |
α) |
Είναι τοποθετημένος με το επίπεδό του κάθετο στις δυναμικές γραμμές του πεδίου. |
| |
β) |
Το επίπεδό του είναι παράλληλο στις δυναμικές γραμμές. |
| |
γ) |
Η κάθετη στο επίπεδό του σχηματίζει με τις δυναμικές γραμμές του πεδίου γωνία 60o. |
| |
[Απ: α) 62,8 Νm2/C, β) 0, γ) 31,4 Νm2/C ] |
|
| 44 |
Μια κλειστή επιφάνεια περικλείει φορτίο 10μC. Ποια είναι η ηλεκτρική ροή που περνάει από την επιφάνεια;
Δίνεται: εo = 8,85x10-12 C2/(Nm2).
[Απ: 1,13x106 Νm2/C ] |
| |
|
| 45 |
Η ηλεκτρική ροή που διέρχεται από μια κλειστή επιφάνεια είναι Φ=2Νm2/C. Υπολογίστε το φορτίο που περικλείει η επιφάνεια.
Δίνεται : εo = 8,85x10-12 C2/(Nm2).
[Απ: 17,7x10-12 C ] |
| |
|
| 46 |
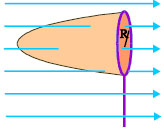
Μια απόχη είναι τοποθετημένη μέσα σε ομογενές ηλεκτρικό πεδίο έντασης Ε με τρόπο ώστε η κυκλική στεφάνη της να είναι κάθετη στις δυναμικές γραμμές του (σχ. 3.55). Υπολογίστε την ηλεκτρική ροή που διέρχεται από τη επιφάνεια που ορίζει το δίχτυ της απόχης. Δίνονται η ένταση Ε του πεδίου και η ακτίνα R της κυκλικής στεφάνης της απόχης.
[ Απ: -EπR2 ] |
| |
|
| 47 |
Όπως γνωρίζετε, στην ατμόσφαιρα υπάρχει ηλεκτρικό πεδίο. Τις ημέρες με καλοκαιρία το πεδίο είναι ασθενές. Αν μια τέτοια μέρα το πεδίο, κοντά στην επιφάνεια της Γης, έχει μέτρο Ε=100Ν/C, κατεύθυνση κατακόρυφη προς τα κάτω, και υποθέσουμε ότι είναι παντού (σε όλη την επιφάνεια της Γης) το ίδιο, υπολογίστε το φορτίο που φέρει η Γη. Δίνεται η ακτίνα της Γης RΓ = 6400 km και η σταθερά εo = 8,85x10-12 C2/(Nm2).
[Απ: -455.295 C ] |
| |
|
| 48 |
Ένας λεπτός σφαιρικός φλοιός ακτίνας R=20cm φέρει ηλεκτρικό φορτίο Q=24μC, ομοιόμορφα κατανεμημένο στην επιφάνειά του. Να υπολογιστεί η ένταση του ηλεκτρικού πεδίου σε σημεία που απέχουν από το κέντρο του
α) r1 = 40 cm, και
β) r2 = 10 cm.
Δίνεται : εo = 8,85x10-12 C2/(Nm2).
[Απ: α) 1,35x106 Ν/C ] β) μηδέν ] |
| |
|
| 49 |
Μια σφαίρα ακτίνας R=1m, από μονωτικό υλικό, φέρει φορτίο Q=12μC, ομοιόμορφα κατανεμημένο σε ολόκληρο τον όγκο της. Πόση είναι η ηλεκτρική ροή που διέρχεται από μια σφαιρική επιφάνεια, ομόκεντρη με τη φορτισμένη σφαίρα, ακτίνας
α) 20 cm β) 60 cm γ) 80 cm δ) 1,2m ε) 2m;
Ο όγκος σφαίρας ακτίνας r υπολογίζεται από τη σχέση V = 4/3 πr3
Δίνεται : εo = 8,85x10-12 C2/(Nm2).
[Απ: α) 10,8x103 Nm2/C β) 29,2x104 Νm2/C γ) 69,4x104 Nm2/C
δ) 135x104 Νm2/C, ε) 135x104 Νm2/C]
|
| |
|
| 50 |
Ένα σύρμα πολύ μεγάλου μήκους έχει φορτίο 4μC ανά μέτρο μήκους του. Υπολογίστε την ένταση του ηλεκτρικού πεδίου που δημιουργεί το σύρμα σε απόσταση α) 10 cm και β) 20 cm από το σύρμα.
Δίνεται : εo = 8,85x10-12 C2/(Nm2).
[Απ: 720x103 Ν/C, 360x103 Ν/C ] |
| |
|
|
 Σχ. 5.55 Σχ. 5.55
|
|
| Δυναμικό του ηλεκτρικού πεδίου - ενέργεια συστήματος φορτίων |
| |
|
| 51 |
Σημειακό φορτίο Q = 2x10-7C δημιουργεί πεδίο που σε ένα σημείο του Α έχει δυναμικό V=300V. Να υπολογιστεί η απόσταση του σημείου Α από το φορτίο. Δίνεται η σταθερά Kc = 9x109Ν m2 /C2.
[ Απ: 6m ]
|
| |
|
| 52 |
Σημειακό φορτίο q = 2x10-8C βρίσκεται τοποθετημένο στο ευθύγραμμο τμήμα ΑΒ, μήκους 3m σε απόσταση 2m από το Α (μεταξύ των Α και Β). Υπολογίστε τη διαφορά δυναμικού VA-VB.
Δίνεται η σταθερά Kc = 9x109Ν m2 /C2. [ Απ: -90V ] |
| |
|
| 53 |
Το πεδίο που δημιουργεί ένα σημειακό φορτίο Q σε ένα σημείο Α έχει ένταση Ε=60 N/C και δυναμικό V=180 V. Να υπολογίσετε το φορτίο και την απόσταση του σημείου Α από το σημειακό φορτίο Q. Δίνεται η σταθερά Kc = 9x109Ν m2/C2. [ Απ: 6x10-8C, 3m ] |
| |
|
| 54 |
Σημειακό φορτίο Q = 2×10-6C, βρίσκεται στο σημείο Α. Να υπολογίσετε το έργο της δύναμης του ηλεκτρικού πεδίου κατά τη μετακίνηση φορτίου q=10-8C από ένα σημείο Β, το οποίο απέχει r1=(ΑΒ)=1cm από το φορτίο Q, σε σημείο Γ, το οποίο απέχει r2=(ΑΓ)=4cm από το Q. Δίνεται: Kc = 9x109Ν m2 /C2.
[ Aπ: 13,5x10-3 J ] |
| |
|
| 55 |
Στις κορυφές Β και Γ, ορθογωνίου τριγώνου ΑΒΓ, με Â=90o, βρίσκονται τα φορτία Q1=4x10-8 C και Q2= 2x10-8 C. Αν ΑΒ=3cm και ΑΓ=4cm, να υπολογιστούν:
α) Τα δυναμικά στα σημεία Α και Μ, όπου Μ το μέσον της ΒΓ.
β) Το έργο που παράγεται από το ηλεκτρικό πεδίο κατά τη
μετακίνηση φορτίου 2×10-10 C από το σημείο Α στο Μ.
Δίνεται: Kc = 9x109Ν m2 /C2.
[ Aπ: 23250V, 32400V, -183x10-8 J ] |
| |
|
| 56 |
Σε κάθε κορυφή ενός ισόπλευρου τριγώνου ΑΒΓ, πλευράς α=30cm, βρίσκεται φορτίο q=2μC. Να υπολογιστεί η ενέργεια του συστήματος των τριών φορτίων. Δίνεται: Kc = 9x109Ν m2 /C2.
[ Aπ: 36x10-2 J ] |
| |
|
| 57 |
Ακίνητο σημειακό φορτίο Q=100μC, βρίσκεται στο σημείο Α. Μικρή σφαίρα με μάζα m=10g και φορτίο q=20nC βρίσκεται στο σημείο Β, στο ίδιο οριζόντιο επίπεδο με το Α και σε απόσταση r1=30 cm από αυτό. Αν η σφαίρα που βρίσκεται στο σημείο Β αφεθεί ελεύθερη, λόγω της απωστικής δύναμης που δέχεται, κινείται χωρίς τριβές. Να υπολογίσετε την ταχύτητά της:
α) Όταν βρίσκεται σε απόσταση r2=60cm από το Α.
β) Όταν βρίσκεται σε πολύ μεγάλη απόσταση από το σημείο Α.
Δίνεται: Kc = 9x109Ν m2 /C2.
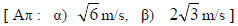 |
|
| Ομογενές ηλεκτρικό πεδίο |
| |
|
| 58 |
Σε ομογενές ηλεκτρικό πεδίο, κατά μήκος μιας δυναμικής γραμμής, βρίσκονται, διαδοχικά, τα σημεία Α, Β και Γ. Εάν VA-VB=5V και οι αποστάσεις μεταξύ των σημείων είναι ΑΒ= x και ΒΓ= x, ποια είναι η διαφορά δυναμικού ανάμεσα στα σημεία Α-Γ και Β-Γ;
[ Απ: 10V, 5V ]
|
| |
|
| 59 |
Ο αέρας είναι μονωτής, αλλά για ηλεκτρικό πεδίο έντασης μεγαλύτερης από 3x106V/m γίνεται αγωγός (δημιουργείται ηλεκτρικός σπινθήρας). Η απόσταση μεταξύ των ηλεκτροδίων σε ένα μπουζί είναι περίπου 0,5mm. Πόση είναι η ελάχιστη διαφορά δυναμικού που πρέπει να εφαρμοστεί στα ηλεκτρόδια, ώστε να παραχθεί ηλεκτρικός σπινθήρας; Θεωρήστε το πεδίο που δημιουργείται ανάμεσα στα ηλεκτρόδια ομογενές.
[ Απ: 1500 V ] |
| |
|
| 60 |
Στο ομογενές ηλεκτρικό πεδίο που υπάρχει ανάμεσα σε δυο οριζόντιες πλάκες με φορτία +Q και –Q, αιωρείται (ισορροπεί) σωματίδιο μάζας m=10-3kg και φορτίου q = 5x10-7C. Αν οι δύο πλάκες απέχουν μεταξύ τους απόσταση l=2cm, να υπολογιστεί η διαφορά δυναμικού που παρουσιάζουν. Δίνεται: g = 10m/s2.
[ Απ: 400 V ] |
| |
|
| 61 |
Ανάμεσα σε δύο παράλληλες κατακόρυφες μεταλλικές πλάκες, που είναι φορτισμένες με φορτία +Q και -Q, ισορροπεί μια μικρή φορτισμένη σφαίρα εκκρεμούς, σε θέση τέτοια ώστε το νήμα του να σχηματίζει γωνία 6o με την κατακόρυφo. Οι δύο παράλληλες μεταλλικές πλάκες απέχουν απόσταση d=10cm και παρουσιάζουν διαφορά δυναμικού V=200V. H σφαίρα του εκκρεμούς έχει μάζα m=2mg. Nα υπολογιστεί το φορτίο της σφαίρας. Δίνονται: g = 10m/s2, εφ6o=0,1.
[ Aπ: 10-9 C ] |
| |
|
| 62 |
Ηλεκτρόνιο βάλλεται με ταχύτητα υο=2x104m/s παράλληλα στις δυναμικές γραμμές ομογενούς ηλεκτρικού πεδίου έντασης Ε=91V/m.
|
| |
α) |
Να υπολογιστεί η δύναμη που δέχεται το ηλεκτρόνιο και η επιτάχυνση που θα αποκτήσει. |
| |
β) |
Να γραφούν οι σχέσεις που περιγράφουν την κίνησή του μέσα στο πεδίο. Εξετάστε τις περιπτώσεις στις οποίες η ταχύτητα του ηλεκτρονίου είναι Ι) ομόρροπη και ΙΙ) αντίρροπη προς τις δυναμικές γραμμές. |
| |
Δίνονται η μάζα του ηλεκτρονίου me = 9,1x10-31 kg και το στοιχειώδες φορτίο e = 1,6x10-19 C.
[ Aπ: 1,456x10-17 N, 16x1012 m/s2 ] |
| |
|
| 63 |
Ηλεκτρόνιο βάλλεται με ταχύτητα υο ομόρροπη με τις δυναμικές γραμμές ομογενούς ηλεκτροστατικού πεδίου έντασης Ε. Να βρεθεί σε πόσο χρόνο θα μηδενιστεί στιγμιαία η ταχύτητά του, σε πόσο χρόνο θα επιστρέψει στην αρχική του θέση και τι ταχύτητα θα έχει τότε. Σχολιάστε το αποτέλεσμα. Δίνονται η μάζα του ηλεκτρονίου me και το στοιχειώδες φορτίο e.
[ Aπ: mυο/Ee, 2mυο/Ee, -υο] |
|
|
|
| 64 |
Δέσμη ηλεκτρονίων εισέρχεται κάθετα στις δυναμικές γραμμές ομογενούς ηλεκτρικού πεδίου που σχηματίζουν δύο παράλληλες φορτισμένες πλάκες. Αν η ταχύτητα των ηλεκτρονίων της δέσμης είναι υο να βρεθεί η απόκλιση που θα υποστεί η δέσμη από το πεδίο καθώς και η ταχύτητα με την οποία εξέρχονται τα ηλεκτρόνια από το πεδίο. Δίνονται η ταχύτητα υο, το μήκος l των φορτισμένων πλακών, η ένταση Ε του πεδίου, η μάζα του ηλεκτρονίου me και το στοιχειώδες φορτίο e. |
| |
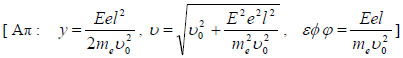 |
| |
| Χωρητικότητα - ενέργεια φορτισμένου πυκνωτή |
| |
|
| 65 |
Πυκνωτής χωρητικότητας 6pF, φορτίζεται σε διαφορά δυναμικού 12V. Να υπολογιστεί το φορτίο του.
[ Απ: 72pC ]
|
| |
|
| 66 |
Οι οπλισμοί επίπεδου πυκνωτή έχουν σχήμα δίσκου ακτίνας 4cm και απέχουν μεταξύ τους 1mm. Τι φορτίο θα αποκτήσει ο πυκνωτής όταν συνδεθεί σε τάση V=10V;
Δίνεται : εo = 8,85x10-12 C2/(Nm2).
[ Απ: 444,6pC ] |
| |
|
| 67 |
Οι οπλισμοί ενός επίπεδου πυκνωτή έχουν εμβαδόν Α=72cm2 και απέχουν μεταξύ τους d=1,2mm. Στον πυκνωτή εφαρμόζεται τάση V=12V. Υπολογίστε.
α) Την ένταση του ηλεκτρικού πεδίου μεταξύ των οπλισμών του.
β) Τη χωρητικότητά του.
γ) Το φορτίο του.
Δίνεται : εo = 8,85x10-12 C2/(Nm2).
[ Απ: 104 V/m, 53,1 pF, 637,2 pC ] |
| |
|
| 68 |
Επίπεδος πυκνωτής με χωρητικότητα C=10μF συνδέεται με πηγή που τον φορτίζει σε τάση V=100V. Χωρίς να απομακρυνθεί ο πυκνωτής από την πηγή διπλασιάζουμε την απόσταση των οπλισμών του. Να υπολογιστούν:
α) Η νέα χωρητικότητα του πυκνωτή.
β) Το φορτίο του πυκνωτή πριν και μετά την απομάκρυνση των οπλισμών του
[ Aπ: 5μF, 1000μC, 500μC ] |
| |
|
| 69 |
Πυκνωτής χωρητικότητας C=20μF φορτίζεται σε τάση V=500V. Πόση ενέργεια μπορεί να δώσει ο πυκνωτής αν εκφορτιστεί;
[ Aπ: 2,5 J ] |
| |
|
| 70 |
Πυκνωτής χωρητικότητας C1=20μF φορτίζεται σε τάση V1=80V. Ο πυκνωτής αποσυνδέεται από την πηγή που τον φόρτισε και συνδέεται με αφόρτιστο πυκνωτή χωρητικότητας C2=5μF. Να υπολογιστούν:
α) Η τάση που θα αποκτήσουν οι δύο πυκνωτές μετά τη σύνδεσή τους.
β) Το φορτίο κάθε πυκνωτή μετά τη σύνδεση
|
| |
γ) |
Η ηλεκτρική δυναμική ενέργεια που θα χαθεί με τη σύνδεση των δύο πυκνωτών. |
| |
[ Aπ: α) 64V, β) 1280μC, 320μC γ) 12,8x10-3 J] |
|
| Διηλεκτρικά |
| |
|
| 71 |
Ανάμεσα στους οπλισμούς πυκνωτή χωρητικότητας C=12μF τοποθετείται διηλεκτρικό με διηλεκτρική σταθερά 5. Να υπολογιστεί η νέα χωρητικότητα του πυκνωτή.
[ Απ: 60μF ]
|
| |
|
| 72 |
Ένας πυκνωτής, χωρίς διηλεκτρικό, φορτίζεται σε τάση 240V. Στη συνέχεια αποσυνδέεται από την πηγή και ανάμεσα στους οπλισμούς του εισάγεται γυαλί, έτσι ώστε να γεμίσει όλος ο χώρος. Παρατηρούμε ότι η τάση του πυκνωτή μειώνεται σε 40V. Να υπολογιστεί η διηλεκτρική σταθερά του γυαλιού.
[ Απ: 6 ] |
| |
|
| 73 |
Πυκνωτής χωρητικότητας C=5μF, χωρίς διηλεκτρικό, συνδέεται με πηγή τάσης V=10V. Διατηρώντας τον πυκνωτή συνδεμένο με την πηγή, γεμίζουμε το χώρο ανάμεσα στους οπλισμούς του με χαρτί. Παρατηρούμε ότι το φορτίο του αυξάνεται κατά ΔQ=150μC. Να υπολογίσετε τη διηλεκτρική σταθερά του χαρτιού.
[ Απ: 4 ] |
| |
|
| 74 |
Θέλουμε να κατασκευάσουμε επίπεδο πυκνωτή με χωρητικότητα C=44nF και τάση λειτουργίας V=2000V. Ως διηλεκτρικό θα χρησιμοποιήσουμε βακελίτη, που έχει διηλεκτρική αντοχή Ε = 24x106 V/m και διηλεκτρική σταθερά Κ=5. Υπολογίστε το ελάχιστο εμβαδόν των οπλισμών του.
Δίνεται : εo = 8,85x10-12 C2/(Nm2).
[ Aπ: 0,083m2 ] |
| |
|
| 75 |
Οι οπλισμοί ενός επίπεδου πυκνωτή έχουν εμβαδόν Α=3cm2. Ανάμεσα στους οπλισμούς του υπάρχει χαρτί, διηλεκτρικής σταθεράς Κ=4. Να υπολογιστεί το μέγιστο φορτίο που μπορεί να φέρει ο πυκνωτής. Δίνονται : εo = 8,85x10-12 C2/(Nm2) και η διηλεκτρική αντοχή του χαρτιού Ε = 16x106 V/m.
[ Aπ: 169,9 nC]
|
| |
|
| Πεδίο βαρύτητας |
| 76 |
Να υπολογιστεί η ένταση και το δυναμικό του πεδίου βαρύτητας της Γης σε ένα σημείο που βρίσκεται σε ύψος h=RΓ από τη επιφάνειά της. Δίνονται η ακτίνα της Γης RΓ = 6400 km και η ένταση του πεδίου βαρύτητας στην επιφάνεια της Γης gο=10 m/s2.
[ Aπ: 2,5 m/s2, -32x106 J/kg ] |
| 77 |
Σώμα μάζας m εκτοξεύεται από την επιφάνεια της Γης κατακόρυφα προς τα πάνω με ταχύτητα υο=103 m/s. Υπολογίστε πόσο ψηλά θα φτάσει το σώμα. Δίνεται η ακτίνα της Γης RΓ = 6400 km και η ένταση του πεδίου βαρύτητας στην επιφάνεια της Γης go=10m/s2. Η αντίσταση του αέρα δε λαμβάνεται υπόψη.
[ Aπ: 50km ] |
|
|
|
| 78 |
Η μάζα της Γης είναι 81 φορές μεγαλύτερη από τη μάζα της Σελήνης και ο λόγος των ακτίνων τους είναι 11/3. |
| |
α) |
Αν η ένταση του πεδίου βαρύτητας στην επιφάνεια της Γης είναι
gο=10Ν/kg να υπολογιστεί η ένταση του πεδίου βαρύτητας στην επιφάνεια της Σελήνης. |
| |
β) |
Ένα σώμα έχει στην επιφάνεια της Γης βάρος 700 Ν. Ποιο θα είναι το βάρος του στην επιφάνεια της Σελήνης; |
| |
[ Απ: 1,66 N/kg , 116,2 N ] |
| |
|
| 79 |
Από διαστημική εξέδρα που βρίσκεται σε ύψος h από την επιφάνεια της Γης θέλουμε να εκτοξεύσουμε διαστημόπλοιο ώστε να εγκαταλείψει το πεδίο βαρύτητας της Γης. Να βρεθεί η ελάχιστη ταχύτητα που πρέπει να δώσουμε στο διαστημόπλοιο. Αγνοήστε τις επιδράσεις των άλλων ουράνιων σωμάτων πλην της Γης . Δίνονται η ακτίνα της Γης RΓ και η ένταση του πεδίου βαρύτητας στην επιφάνειά της gο.
|
| |
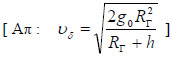 |
| |
|
| 80 |
Να βρείτε την ταχύτητα διαφυγής ενός σώματος από την επιφάνεια πλανήτη με μάζα m=MΓ/8 και πυκνότητα ίση με αυτή της Γης. Η ταχύτητα διαφυγής από τη Γη είναι υ=11,2 km/s. H Γη και ο πλανήτης να θεωρηθούν ομογενείς ακίνητες
|
| |
σφαίρες. Ο όγκος μιας σφαίρας δίνεται από τη σχέση 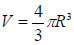 |
| |
[ Απ: 5,6 km/s ] |
| |
|
| 81 |
Η ταχύτητα με την οποία φτάνει ένας μετεωρίτης στη Γη μπορεί να εκτιμηθεί από το μέγεθος του κρατήρα που θα ανοίξει κατά την πρόσκρουσή του στην επιφάνεια της Γης. Από το μέγεθος ενός τέτοιου κρατήρα εκτιμάμε ότι ένας μετεωρίτης έφτασε στην επιφάνεια της Γης με ταχύτητα υ=65.000km/h. Υπολογίστε την ταχύτητα που είχε ο μετεωρίτης όταν έμπαινε στα όρια της βαρυτικής επίδρασης της Γης. Θεωρήστε τις τριβές που αναπτύσσονται κατά την κίνηση του μετεωρίτη στην ατμόσφαιρα της Γης αμελητέες και αγνοήστε την επίδραση των άλλων ουράνιων σωμάτων, πλην της Γης, στην κίνησή του. Δίνονται RΓ=6400 km, και gο=10 m/s2).
[ Απ: 14x103 m / s ] |
| |
|
| 82 |
Δύο μικρές σφαίρες με μάζες m1= m και m2= 2m βρίσκονται σε απόσταση l μεταξύ τους και έξω από οποιοδήποτε πεδίο βαρύτητας. Να βρεθεί το σημείο του χώρου στο οποίο η ένταση του βαρυτικού πεδίου που δημιουργούν οι σφαίρες είναι μηδέν και στη συνέχεια να υπολογισθεί γι’αυτό το σημείο το δυναμικό του βαρυτικού πεδίου. Δίνεται η σταθερά παγκόσμιας έλξης G.
|
| |
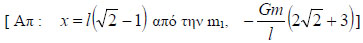 |
| |
|
| 83 |
Στις κορυφές Α,Β, Γ ενός τριγώνου με πλευρές α, β, γ βρίσκονται οι σφαιρικές μάζες m1, m2, και m3. Να υπολογιστεί η ενέργεια που απαιτείται για να τις απομακρύνουμε σε άπειρη απόσταση μεταξύ τους. Δίνεται η σταθερά G.
|
| |
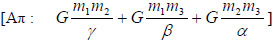 |
|
 Σχ. 5.55
Σχ. 5.55