Φυσική (Β Λυκείου Θετικών Σπουδών) - Βιβλίο Μαθητή (Εμπλουτισμένο)

 
5-10 ΕΝΕΡΓΕΙΑ ΑΠΟΘΗΚΕΥΜΕΝΗ ΣΕ ΦΟΡΤΙΣΜΕΝΟ
ΠΥΚΝΩΤΗ

 

Σε προηγούμενη παράγραφο είδαμε ότι όλες οι διατάξεις φορτίου έχουν ορισμένη ηλεκτρική δυναμική ενέργεια U, ίση με το έργο που απαιτείται για να τοποθετηθούν τα φορτία στις θέσεις τους. Ένας φορτισμένος πυκνωτής έχει δυναμική ενέργεια U η οποία δίνεται από τη σχέση.

 

  U = 1 CV2 (5.46)
2

 

Η ενέργεια του φορτισμένου πυκνωτή αποδίδεται κατά την εκφόρτισή του. Αν ενώσουμε τους δύο οπλισμούς του πυκνωτή με ένα αγωγό θα μετακινηθούν φορτία από τον ένα οπλισμό στον άλλο μέχρι οι δύο οπλισμοί να αποκτήσουν το ίδιο δυναμικό. Τότε λέμε ότι ο πυκνωτής εκφορτίστηκε. Κατά την εκφόρτιση του πυκνωτή η αποθηκευμένη ηλεκτρική δυναμική ενέργεια μετατρέπεται σε θερμότητα στον αγωγό που συνδέει τους οπλισμούς.

Υπολογισμός της ενέργειας φορτισμένου πυκνωτή

           

Για να υπολογίσουμε τη δυναμική ενέργεια που έχει αποθηκευμένη ένας φορτισμένος πυκνωτής, ας φανταστούμε μια υποθετική διαδικασία φόρτισης: Σε ένα αρχικά αφόρτιστο πυκνωτή παίρνουμε μικρές ποσότητες φορτίου  +dq από τον ένα οπλισμό και τις τοποθετούμε στον άλλο. Ο οπλισμός από τον οποίο αφαιρείται θετικό φορτίο θα  φορτιστεί αρνητικά ενώ ο οπλισμός στον οποίο προσθέτουμε θετικό φορτίο, θα φορτιστεί θετικά. Έστω qo, και Vo οι τελικές τιμές για το φορτίο και την τάση του πυκνωτή.

Η μεταφορά του πρώτου φορτίου dq από τον ένα οπλισμό στον άλλο γίνεται χωρίς να καταναλώσουμε έργο. Με την απόσπαση όμως του πρώτου φορτίου +dq από τον ένα οπλισμό και την εγκατάστασή του στον άλλο, ο πρώτος οπλισμός θα έχει φορτίο –dq και ο δεύτερος +dq. Aυτό θα έχει ως αποτέλεσμα τη δημιουργία πεδίου. Τώρα πια, η μεταφορά  νέου φορτίου dq απαιτεί προσπάθεια (έργο), εξ αιτίας της δύναμης dF΄=Edq που ασκεί το πεδίο στο φορτίο. Η δύναμη dF που μετακινεί το φορτίο πρέπει να εξουδετερώσει τη δύναμη dF΄ του πεδίου. Όσο προχωράει η φόρτιση του πυκνωτή, το ηλεκτρικό του πεδίο θα γίνεται πιο ισχυρό και  θα απαιτείται ολοένα και μεγαλύτερο έργο για τη μετακίνηση φορτίου dq. Το έργο της δύναμης dF είναι θετικό και ίσο απολύτως με το έργο της δύναμης dF΄ του πεδίου.

Αν κάποια στιγμή η τάση του πυκνωτή είναι V, το έργο της δύναμης που απαιτείται για τη μετακίνηση φορτίου dq, από τον ένα οπλισμό στον άλλο είναι

  dW = V dq (4.23)

 

Ισχύει     C = q        ή       V =  1 q
V C

Η γραφική παράσταση της σχέσης V = f(q) από την στιγμή που το φορτίο του πυκνωτή είναι μηδέν μέχρι να αποκτήσει την τελική του τιμή qo, είναι ευθεία που περνάει από την αρχή των αξόνων (σχ. 3.37). Από τη γραφική παράσταση παρατηρούμε ότι αν το σχήμα με το μπλε χρώμα μπορεί να θεωρηθεί παραλληλόγραμμο -και μπορεί να θεωρηθεί αν το dq είναι απειροστά μικρό- το εμβαδόν του θα είναι ίσο με V. dq και θα δίνει το έργο που απαιτείται για τη μεταφορά του φορτίου dq. To συνολικό έργο που απαιτείται για να φορτιστεί ο πυκνωτής θα είναι ίσο με το εμβαδόν του τριγώνου από την γραμμή του διαγράμματος μέχρι τον άξονα q, δηλαδή

W = 1 qoVo    ή      W =  1 CVo2
2 2

Επομένως η δυναμική ενέργεια του φορτισμένου πυκνωτή είναι

  U =  1 CVo2  
2

 

 

 

 

 

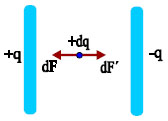Ο πυκνωτής φορτίζεται με την μεταφορά απειροστά μικρών φορτίων dq από τον ένα οπλισμό στον άλλο. Σχ. 5.36 Ο πυκνωτής φορτίζεται με την μεταφορά απειροστά μικρών φορτίων dq από τον ένα οπλισμό στον άλλο.

 

 

 

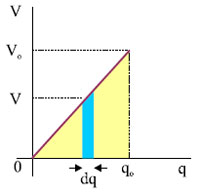Από τη γραφική παρά-σταση της σχέσης V=q/C μπορούμε να υπολογίσουμε την ενέργεια του πυκνωτή. Σχ. 5.37 Από τη γραφική παράσταση της σχέσης V=q/C μπορούμε να υπολογίσουμε την ενέργεια του πυκνωτή.
ΠΑΡΑΔΕΙΓΜΑ 5-10

Πυκνωτής χωρητικότητας C1=4μF, φορτίζεται από την πηγή, τάσης V=20V, με φορτίο Q. Στη συνέχεια ο πυκνωτής αποσυνδέεται από την πηγή και συνδέεται με αφόρτιστο πυκνωτή χωρητικότητας C2=12μF όπως στο σχήμα 3.39:
α) Να υπολογιστεί η κοινή τάση V΄ που θα αποκτήσουν οι πυκνωτές μετά τη σύνδεσή τους.
β) Το φορτίο που θα αποκτήσει κάθε πυκνωτής μετά τη σύνδεση.
γ) Με τη σύνδεση των δυο πυκνωτών μεταβάλλεται η ενέργεια του συστήματος. Πόσο μεταβλήθηκε η ενέργεια; Πού οφείλεται η μεταβολή αυτή;

 

 

Απάντηση:

 

Ο πυκνωτής χωρητικότητας C1, κατά τη σύνδεσή του με την  πηγή απέκτησε φορτίο

  Q = C1V = 80 μC  

 

Μετά την αποσύνδεση της πηγής και τη σύνδεση των δύο πυκνωτών μεταξύ τους, ένα μέρος του φορτίου Q μετακινείται ώστε να φορτιστεί και ο πυκνωτής C2. Οι πυκνωτές C1 και C2 αποκτούν φορτία Q1 και Q2, αντίστοιχα και η ( κοινή) διαφορά δυναμικού στους οπλισμούς γίνεται V΄.

 

α) Σύμφωνα με την αρχή διατήρησης του φορτίου:  
  Q = Q1 + Q2 (5.47)
  Για κάθε ένα από τους πυκνωτές ισχύει:  
  Q1 = C1 V΄ και Q2 = C2 V΄ (5.48)
  Αντικαθιστώντας τις (5.48) στην (5.47) έχουμε:  
  Q = C1 V΄ + C2 V΄   ή   Q = (C1 + C2 ) V΄    επομένως V' =  Q = 5V
C1 + C2

 

β) Αντικαθιστώντας την τιμή του V΄στις σχέσεις (5.48) υπολογίζουμε τα φορτία που απέκτησαν οι πυκνωτές:
  Q1 = 20 μC και Q2 = 60 μC
  Παρατηρούμε ότι ο πυκνωτής με τη μεγαλύτερη χωρητικότητα "κρατάει"  και το περισσότερο φορτίο.
   
γ) Η ενέργεια του συστήματος μεταβλήθηκε  κατά

 

ΔU = Uμετά - Uπρίν = 1 C1 V΄2 + 1  C2 V΄2 - 1   C1 V2 = -6 x 10-4J
2 2 2

 

Το αρνητικό πρόσημο σημαίνει ότι η ενέργεια του συστήματος ελαττώθηκε. Η ηλεκτρική ενέργεια που χάθηκε από το σύστημα έγινε θερμότητα στους αγωγούς κατά τη μετακίνηση φορτίου από τον ένα πυκνωτή στον άλλο.
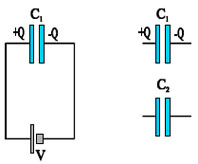Σχ. 5.38 Σχ. 5.38

 

 

 

 

 

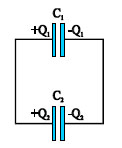Σχ. 5.39 Σχ. 5.39