4-9 ΕΦΑΡΜΟΓΗ ΤΟΥ ΠΡΩΤΟΥ ΘΕΡΜΟΔΥΝΑΜΙΚΟΥ
ΝΟΜΟΥ ΣΕ ΕΙΔΙΚΕΣ ΠΕΡΙΠΤΩΣΕΙΣ Α) Ισόθερμη αντιστρεπτή μεταβολή
Έστω μια ισόθερμη αντιστρεπτή μεταβολή ορισμένης ποσότητας αερίου από την αρχική κατάσταση Α, όγκου Vα, στην τελική κατάσταση Β, όγκου Vτ. Η μεταβολή γίνεται σε σταθερή θερμοκρασία Τ. Το σχήμα 2.11 παριστάνει γραφικά τη μεταβολή. Το εμβαδόν κάτω από την γραμμή του διαγράμματος είναι ίσο με το έργο που παράγει το αέριο. Από τον υπολογισμό του εμβαδού, που δεν είναι δυνατόν να γίνει χωρίς τη χρήση ολοκληρωμάτων, προκύπτει ότι
Επειδή η θερμοκρασία του αερίου δε μεταβάλλεται, UA=UB επομένως ΔU=0, οπότε ο πρώτος θερμοδυναμικός νόμος, στην ισόθερμη μεταβολή, παίρνει τη μορφή
Στην ισόθερμη εκτόνωση όλο το ποσό θερμότητας που απορροφά το αέριο μετατρέπεται σε μηχανικό έργο. |
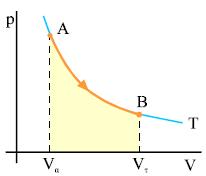
Σχ. 4.11 Το διάγραµµα παριστάνει την ισόθερµη εκτόνωση ενός αερίου από την αρχική κατάσταση Α στην τελική κατάσταση Β. |
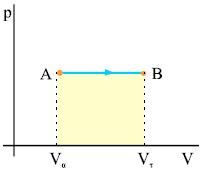
 Σχ. 4.12 Η ισόχωρη μεταβολή ενός αερίου από την κατάσταση Α στην κατάσταση Β. Σχ. 4.12 Η ισόχωρη μεταβολή ενός αερίου από την κατάσταση Α στην κατάσταση Β.
 Σχ. 4.13 Η ισόβαρής μεταβολή ενός αερίου από την κατάσταση Α στην κατάσταση Β. Σχ. 4.13 Η ισόβαρής μεταβολή ενός αερίου από την κατάσταση Α στην κατάσταση Β.
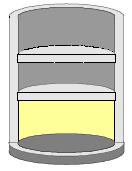 Σχ. 4.14 Τα τοιχώματα του δοχείου καθώς και το έμβολο είναι από μονωτικό υλικό. Στη διάρκεια της μεταβολής το αέριο δεν ανταλλάσσει θερμότητα με το περιβάλλον. Σχ. 4.14 Τα τοιχώματα του δοχείου καθώς και το έμβολο είναι από μονωτικό υλικό. Στη διάρκεια της μεταβολής το αέριο δεν ανταλλάσσει θερμότητα με το περιβάλλον. |
Β) Ισόχωρη αντιστρεπτή μεταβολή
Έστω η ισόχωρη αντιστρεπτή μεταβολή μιας ποσότητας αερίου, από την κατάσταση Α στην κατάσταση Β. Το αέριο θερμαίνεται με σταθερό όγκο και η θερμοκρασία του αυξάνεται. Το σχήμα 2.12 παριστάνει γραφικά τη μεταβολή. Από το σχήμα φαίνεται ότι το έργο του αερίου είναι μηδέν. Αυτό είναι αναμενόμενο γιατί έργο έχουμε μόνο όταν ο όγκος του αερίου μεταβάλλεται.
Στην ισόχωρη θέρμανση όλο το ποσό θερμότητας που απορρόφησε το αέριο χρησιμοποιήθηκε για την αύξηση της εσωτερικής του ενέργειας.
Γ) Ισοβαρής αντιστρεπτή μεταβολή
Ένα αέριο θερμαίνεται ισοβαρώς από την αρχική κατάσταση Α, όγκου Vα , στην τελική κατάσταση Β, όγκου Vτ . Το σχήμα 2.13 παριστάνει γραφικά τη μεταβολή. Το εμβαδόν κάτω από την γραμμή του διαγράμματος δίνει το έργο του αερίου.
Ο πρώτος θερμοδυναμικός νόμος παίρνει τη μορφή
Στην ισοβαρή θέρμανση ένα μέρος από το ποσό θερμότητας που απορρόφησε το αέριο από το περιβάλλον χρησιμοποιήθηκε για την αύξηση της εσωτερικής του ενέργειας και το υπόλοιπο αποδόθηκε εκ νέου στο περιβάλλον με τη μορφή έργου
Δ) Αδιαβατική μεταβολή
Αδιαβατική ονομάζουμε τη μεταβολή κατά την οποία δε συντελείται μεταφορά θερμότητας από το περιβάλλον προς το σύστημα ή αντίστροφα.
Έστω ένα αέριο που εκτονώνεται με αντιστρεπτό τρόπο μέσα σε δοχείο με έμβολο από την κατάσταση Α (pα, Vα) στην κατάσταση Β (pτ, Vτ) (Σχ. 4.14). Το δοχείο και το έμβολο είναι κατασκευασμένα έτσι ώστε να μην επιτρέπουν την ανταλλαγή θερμότητας ανάμεσα στο αέριο και στο περιβάλλον (ένα τέτοιο δοχείο είναι το θερμός που χρησιμοποιούμε στα σπίτια μας). Η μεταβολή αυτή είναι μια αντιστρεπτή αδιαβατική μεταβολή.
Ο νόμος που διέπει τη μεταβολή είναι
|
όπου γ ένας καθαρός αριθμός, μεγαλύτερος της μονάδας, που εξαρτάται από την ατομικότητα του αερίου και από το είδος των δεσμών που συγκρατούν τα άτομα στο μόριο. Για τον αριθμό αυτό θα μιλήσουμε στην επόμενη ενότητα.
Εφαρμόζοντας τον πρώτο θερμοδυναμικό νόμο και λαμβάνοντας υπόψη ότι Q=0 προκύπτει
Στην αδιαβατική µεταβολή το έργο είναι ίσο µε το αντίθετο της µεταβολής της εσωτερικής ενέργειας.
Επειδή στη μεταβολή που περιγράψαμε το έργο είναι θετικό, από τη σχέση (4.7) προκύπτει ότι η εσωτερική ενέργεια μειώνεται, επομένως το αέριο ψύχεται. Το σχήμα 2.15 παριστάνει την αντιστρεπτή αδιαβατική μεταβολή που περιγράψαμε. Επειδή η τελική θερμοκρασία είναι μικρότερη από την αρχική, η καμπύλη της έχει μεγαλύτερη κλίση από την ισόθερμη που περνάει από το σημείο Α. Στην αδιαβατική μεταβολή το έργο μπορεί να υπολογιστεί από τη σχέση
Στην πράξη όταν ένα αέριο συμπιέζεται (ή εκτονώνεται) πολύ γρήγορα, πολύ μικρό ποσό θερμότητας μετακινείται από το αέριο προς το περιβάλλον ή αντίστροφα. Η διεργασία αυτή είναι σχεδόν αδιαβατική. Τέτοιες διεργασίες συμβαίνουν στον κύλινδρο του βενζινοκινητήρα. E)Κυκλική αντιστρεπτή μεταβολή
Κυκλική ονομάζουμε μια μεταβολή στην οποία το σύστημα μετά από μια διεργασία επιστρέφει στην ίδια κατάσταση.
Το σχήμα 2.16 παριστάνει μια κυκλική αντιστρεπτή μεταβολή ορισμένης ποσότητας αερίου. Το αέριο αρχικά βρισκόταν στην κατάσταση Α και μετά από μια διεργασία επιστρέφει πάλι στην αρχική κατάσταση Α.
Το έργο του αερίου μπορεί να υπολογιστεί ως εξής: Το έργο του αερίου κατά τη μεταβολή από το Α στο Β είναι ίσο με το εμβαδόν του τμήματος που είναι σκιασμένο με κόκκινο και είναι θετικό, γιατί το αέριο εκτονώνεται. Το έργο, κατά τη μεταβολή από το Β στο Α, είναι ίσο με το εμβαδόν του τμήματος που είναι σκιασμένο με πράσινο και είναι αρνητικό γιατί το αέριο συμπιέζεται. Το έργο του αερίου σε ολόκληρη την κυκλική μεταβολή που είναι το αλγεβρικό άθροισμα αυτών των έργων, είναι ίσο με το εμβαδόν που περικλείει η κλειστή γραμμή που περιγράφει τη μεταβολή. 
|
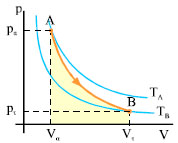 Σχ. 4.15 Ένα αέριο εκτονώνεται αδιαβατικά από την αρχική κατάσταση Α στην τελική κατάσταση Β. Σχ. 4.15 Ένα αέριο εκτονώνεται αδιαβατικά από την αρχική κατάσταση Α στην τελική κατάσταση Β.
Σχ. 4.16 Το σχήμα α παριστάνει γραφικά μια αντιστρεπτή κυκλική μεταβολή. Το εμβαδόν της χρωματισμένης επιφάνειας στο σχήμα β δίνει το έργο του αερίου κατά την μεταβολή Α→Β. Το έργο κατά τη μεταβολή Β→Α είναι κατ' απόλυτη τιμή ίσο με το εμβαδόν της χρωματι-σμένης επιφάνειας στο σχήμα γ, η αλγεβρική του τιμή όμως είναι αρνητική. Το συνολικό έργο προκύπτει αν από το εμβαδόν του σχήματος β αφαιρέσουμε το εμβαδόν του σχήματος γ. Από την αφαίρεση αυτή προκύπτει το εμβαδόν που περικλείει η γραμμή του διαγράμματος (σχ. δ). |
|
Το ολικό έργο σε μια κυκλική αντιστρεπτή μεταβολή είναι ίσο με το εμβαδόν που περικλείεται από τη γραμμή του διαγράμματος, στη γραφική παράσταση p-V.
Εάν η κυκλική μεταβολή διαγραφόταν κατά την αντίθετη φορά, για να υπολογίσουμε το έργο θα αφαιρούσαμε από το μικρό εμβαδόν το μεγάλο. Έτσι, το συνολικό έργο θα ήταν αρνητικό. Επομένως σε μια αντιστρεπτή κυκλική μεταβολή, το έργο είναι θετικό όταν η γραφική παράσταση της μεταβολής διαγράφεται με την φορά των δεικτών του ρολογιού και αρνητικό όταν διαγράφεται με την αντίθετη φορά. Επειδή το αέριο επιστρέφει στην αρχική του κατάσταση, η μεταβολή στην εσωτερική του ενέργεια είναι μηδέν ΔU = 0. Εφαρμόζοντας τον πρώτο θερμοδυναμικό νόμο στην κυκλική μεταβολή έχουμε
Στην κυκλική μεταβολή η θερμότητα που απορροφά ή αποδίδει το αέριο ισούται με το έργο που παράγει ή δαπανά. |