4-15 ΥΠΟΛΟΓΙΣΜΟΣ ΤΗΣ ΜΕΤΑΒΟΛΗΣ ΤΗΣ
ΕΝΤΡΟΠΙΑΣ ΣΕ ΜΕΡΙΚΕΣ ΠΕΡΙΠΤΩΣΕΙΣ Αδιαβατική αντιστρεπτή μεταβολή Έστω ότι ένα αέριο, που βρίσκεται αρχικά στην κατάσταση Α (pA, VA, TA), εκτονώνεται αδιαβατικά μέχρι την κατάσταση Β (pB, VB, TB). Η μεταβολή του αερίου παριστάνεται γραφικά στο σχήμα 2.28.
Επειδή πρόκειται για αντιστρεπτή μεταβολή, η μεταβολή της εντροπίας ΔSAB, μπορεί να υπολογιστεί αν χωρίσουμε την διεργασία σε στοιχειώδεις μεταβολές, υπολογίσουμε την μεταβολή της εντροπίας σε κάθε στοιχειώδη μεταβολή και αθροίσουμε όλους του όρους.
Όµως στην αδιαβατική µεταβολή το αέριο δεν ανταλλάσσει θερµότητα µε το περιβάλλον, εποµένως όλοι οι αριθµητές στo δεύτερο µέλος της παραπάνω σχέσης είναι µηδέν, µε αποτέλεσµα
Όµως στην αδιαβατική µεταβολή το αέριο δεν ανταλλάσσει θερµότητα µε το περιβάλλον, εποµένως όλοι οι αριθµητές στo δεύτερο µέλος της παραπάνω σχέσης είναι µηδέν, µε αποτέλεσµα
Στην αδιαβατική αντιστρεπτή μεταβολή η εντροπία δε μεταβάλλεται.
|
 Σχ. 4.28 Ένα αέριο εκτονώνεται αδιαβατικά από την αρχική κατάσταση Α στην τελική κατάσταση Β. Η εντροπία του παραμένει σταθερή Σχ. 4.28 Ένα αέριο εκτονώνεται αδιαβατικά από την αρχική κατάσταση Α στην τελική κατάσταση Β. Η εντροπία του παραμένει σταθερή |
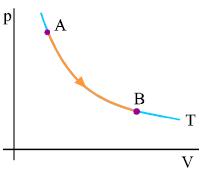 Σχ. 4.29 Το αέριο εκτονώνεται ισόθερμα από την αρχική κατάσταση Α στην τελική κατάσταση Β. Η εντροπία του αερίου αυξάνεται. Σχ. 4.29 Το αέριο εκτονώνεται ισόθερμα από την αρχική κατάσταση Α στην τελική κατάσταση Β. Η εντροπία του αερίου αυξάνεται.
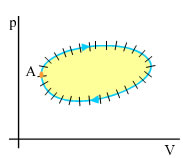 Σχ. 4.30 Αν χωρίσουμε την κυκλική αντιστρεπτή μεταβολή σε στοιχειώδεις, τότε το άθροισμα των dS, σε όλη την κυκλική διαδρομή, είναι μηδέν. Σχ. 4.30 Αν χωρίσουμε την κυκλική αντιστρεπτή μεταβολή σε στοιχειώδεις, τότε το άθροισμα των dS, σε όλη την κυκλική διαδρομή, είναι μηδέν.
|
Ισόθερμη αντιστρεπτή μεταβολή Έστω ένα αέριο που βρίσκεται αρχικά στην κατάσταση Α και εκτονώνεται ισόθερμα σε θερμοκρασία Τ μέχρι την κατάσταση Β. Το σχήμα 2.29 αποδίδει γραφικά τη μεταβολή του αερίου. Και εδώ επειδή η διεργασία είναι αντιστρεπτή η μεταβολή της εντροπίας υπολογίζεται όπως πριν.
Το άθροισμα στον αριθμητή δίνει το συνολικό ποσό θερμότητας Q που απορρόφησε το αέριο κατά την μεταβολή. Έτσι, η σχέση γίνεται:
Στην ισόθερμη μεταβολή η θερμότητα που ανταλλάσσει το αέριο με το
Κυκλική μεταβολή
Εφ΄ όσον σε μια κυκλική μεταβολή - αντιστρεπτή ή όχι - το σύστημα επιστρέφει στην αρχική του κατάσταση, η εντροπία του συστήματος δε μεταβάλλεται.
Στην περίπτωση που η κυκλική μεταβολή είναι αντιστρεπτή, αν τη χωρίσουμε σε ν στοιχειώδη τμήματα, ώστε σε καθένα από αυτά να μπορούμε να θεωρήσουμε ότι η θερμοκρασία είναι σταθερή, θα ισχύει:
όπου ΔQ1, ΔQ2, ...,ΔQν τα στοιχειώδη ποσά θερμότητας που προσλαμβάνει ή αποδίδει το σύστημα σε κάθε στοιχειώδες τμήμα της μεταβολής. Σε μία κυκλική αντιστρεπτή μεταβολή λοιπόν ισχύει και
|
Ελεύθερη εκτόνωση Ένα θερμικά μονωμένο δοχείο χωρίζεται με μεμβράνη σε δύο χώρους. O ένας περιέχει αέριο σε θερμοκρασία Τ και ο άλλος είναι κενός. Κάποια στιγμή η μεμβράνη σπάει και το αέριο εκτονώνεται και καταλαμβάνει αστραπιαία τον όγκο ολόκληρου του δοχείου (σχ.. 2.31). Η διαδικασία εκτόνωσης είναι πολύ βίαιη και με κανένα τρόπο δε μπορεί να χαρακτηριστεί αντιστρεπτή. Θα υπολογίσουμε τη μεταβολή της εντροπίας του αερίου. Μη βιαστείτε να πείτε ότι, αφού το αέριο δεν ανταλλάσσει θερμότητα με το περιβάλλον, σύμφωνα με τη (4.26), θα είναι ΔS=0. Η (4.26) ισχύει μόνο για αντιστρεπτές μεταβολές. Αφού η μεταβολή είναι μη αντιστρεπτή δεν μπορεί να παρασταθεί γραφικά. Γραφικά μπορούν να απεικονισθούν μόνο η αρχική και τελική κατάσταση Α και Β του αερίου, που είναι καταστάσεις ισορροπίας (Σχ. 4.32α). Το έργο που παράγει το αέριο για να καταλάβει τον κενό χώρο είναι μηδενικό και, όπως είπαμε, τα τοιχώματα του δοχείου δεν επιτρέπουν τη μεταφορά θερμότητας. Από τον πρώτο θερμοδυναμικό νόμο (Q = ΔU + W) προκύπτει ΔU = 0. Η εσωτερική ενέργεια του αερίου εξαρτάται μόνο από την αρχική και τελική θερμοκρασία και, αφού η εσωτερική ενέργεια δε μεταβάλλεται, η τελική θερμοκρασία του αερίου είναι ίση με την αρχική Τ. Επειδή ΤA = ΤB = Τ η αρχική κατάσταση (Α) και η τελική κατάσταση (Β), βρίσκονται πάνω στην ίδια ισόθερμη καμπύλη (σχ. 2.32β).
Για να υπολογίσουμε τη μεταβολή της εντροπίας θα εκμεταλλευτούμε το ότι αυτή εξαρτάται μόνο από την αρχική και τελική κατάσταση του συστήματος. Μια αντιστρεπτή διαδικασία που έχει τα ίδια άκρα Α και Β είναι η ισόθερμη αντιστρεπτή μεταβολή από την κατάσταση Α στη Β.

Τέλος, επειδή VB > VΑ, η εντροπία του αερίου αυξάνεται (ΔS > 0). Το αποτέλεσμα μπορούσαμε να το προβλέψουμε, αφού στις πραγματικές (μη αντιστρεπτές) μεταβολές η εντροπία ενός απομονωμένου συστήματος αυξάνεται μέχρις ότου το σύστημα έρθει σε κατάσταση θερμοδυναμικής ισορροπίας. |
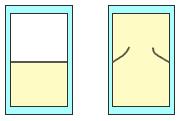 Σχ. 4.31 Ελεύθερη εκτόνωση αερίου. Όταν διαρραγεί η μεμβράνη η οποία περιορίζει το αέριο, το αέριο εκτονώνεται ελεύθερα με μη αντιστρεπτό τρόπο και καταλαμβάνει όλο τον όγκο του δοχείου. Σχ. 4.31 Ελεύθερη εκτόνωση αερίου. Όταν διαρραγεί η μεμβράνη η οποία περιορίζει το αέριο, το αέριο εκτονώνεται ελεύθερα με μη αντιστρεπτό τρόπο και καταλαμβάνει όλο τον όγκο του δοχείου.
Σχ. 4.32 Η μεταβολή κατά την ελεύθερη εκτόνωση είναι μη αντιστρεπτή. Γραφικά μπορούν να παρασταθούν μόνο η αρχική και τελική κατάσταση του αερίου Α και Β. Επειδή κατά την ελεύθερη εκτόνωση η αρχική θερμοκρασία του αερίου είναι ίση με την τελική, η αρχική και η τελική κατάσταση του αερίου βρίσκονται πάνω στην ίδια ισόθερμη.
|