3-5 ΤΑ ΠΡΩΤΑ ΣΗΜΑΝΤΙΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ

Σχέση πίεσης (p) και θερµοκρασίας (Τ) µε τις ταχύτητες των µορίων.

Βασισμένοι στις παραπάνω παραδοχές καταφέραμε να βρούμε σχέσεις που συνδέουν τα μακροσκοπικά μεγέθη, όπως η πίεση και η θερμοκρασία, που μέχρι τώρα μπορούσαμε να τα προσδιορίσουμε μόνο πειραματικά, με τις μέσες τιμές των ταχυτήτων των μορίων του αερίου.

Η πίεση είναι το μονόμετρο μέγεθος που ορίζεται ως το πηλίκο του μέτρου της δύναμης που ασκείται κάθετα σε κάποια επιφάνεια προς το εμβαδόν της επιφάνειας (Σχ. 3.5).

p	=	ΔF

		ΔA

Στην περίπτωση ενός αερίου που είναι κλεισμένο σ' ένα δοχείο η πίεση που ασκείται στα τοιχώματα του δοχείου οφείλεται στις δυνάμεις που ασκούν τα μόρια του αερίου στα τοιχώματα κατά τις κρούσεις τους με αυτά (Σχ. 3.6).

Η πρώτη σχέση που προκύπτει από την εφαρμογή των νόμων της μηχανικής και των παραδοχών της κινητικής θεωρίας, είναι αυτή που συνδέει την πίεση (p) του αερίου με τις ταχύτητες των μορίων του αερίου.
Βρέθηκε συγκεκριμένα ότι

(3.4)

όπου	Ν	ο αριθμός των μορίων του αερίου,
	m	η μάζα κάθε μορίου,
	V	o όγκος του δοχείου και
		η μέση τιμή των τετραγώνων των ταχυτήτων των μορίων του αερίου.

Η απόδειξη της σχέσης (3.4) γίνεται στο τέλος της παραγράφου

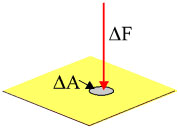Σχ. 3.5 Το ΔΑ είναι ένα στοιχειώδες τμήμα της επιφάνειας και ΔF η δύναμη που ασκείται σε αυτό.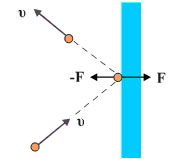

Σχ. 3.6 Η κρούση του μορίου με το τοίχωμα θεωρείται ελαστική. Το μέτρο της ταχύτητας του μορίου είναι το ίδιο πριν και μετά την κρούση.

Μια άλλη, πιο κομψή, μορφή της σχέσης (3.4) προκύπτει αν λάβουμε υπόψη ότι το γινόμενο Νm είναι η ολική μάζα του αερίου, και ότι το πηλίκο της ολικής μάζας προς τον όγκο V που καταλαμβάνει το αέριο είναι η πυκνότητα ρ του αερίου, οπότε: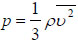

Πολλαπλασιάζοντας και διαιρώντας το δεύτερο μέλος της (3.4) με τον αριθμό 2 προκύπτει η παρακάτω μορφή που συνδέει την πίεση με τη μέση κινητική ενέργεια των μορίων.

(3.5)

Από την (3.5) προκύπτει

(3.6)

Όμως από την καταστατική εξίσωση γνωρίζουμε ότι

pV	=	nRT	=	N	R T

				N_A

όπου Ν_Α ο αριθμός των μορίων ανά mol (σταθερά Avogadro).

Το πηλίκο	R	εμφανίζεται συχνά στην κινητική θεωρία. Είναι το πηλίκο δύο

	N_A

σταθερών, ονομάζεται σταθερά του Boltzmann (Μπόλτζμαν) και συμβολίζεται με το k.

k	=	R	= 1,381x10^-23J /(μόριο·Κ)

		N_A

Μπορούμε λοιπόν να γράψουμε την καταστατική και ως εξής:

pV = NkT

(3.7)

Εξισώνοντας τα δεύτερα μέλη των σχέσεων (3.6) και (3.7) και λύνοντας ως προς Τ βρίσκουμε

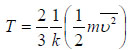Η σχέση αυτή είναι πολύ σημαντική γιατί συνδέει τη θερμοκρασία με τη μέση μεταφορική κινητική ενέργεια των μορίων του αερίου.
Από τη σχέση αυτή, για τη μέση κινητική ενέργεια των μορίων βρίσκουμε

(3.8)

Η τετραγωνική ρίζα της εικόνα ονομάζεται ενεργός ταχύτητα και συμβολίζεται υ_εν. Από τη σχέση (3.8) προκύπτει

(3.9)

Απόδειξη της σχέσης

Θεωρούμε ένα κυβικό δοχείο ακμής d. (Σχ. 3.7). Το δοχείο θα έχει όγκο V = d³ και εμβαδόν έδρας A = d². Υποθέτουμε ότι στο δοχείο περιέχεται πολύ μεγάλος αριθμός Ν πανομοιότυπων μορίων αερίου, μάζας m το καθένα, που πληρούν τις προϋποθέσεις της προηγούμενης παραγράφου. Τα τοιχώματα του δοχείου είναι τελείως άκαμπτα, έχουν πολύ μεγάλη μάζα και δε μετακινούνται.

Κατά τη διάρκεια των κρούσεων των μορίων στα τοιχώματα, τα μόρια ασκούν δυνάμεις σ’ αυτά. Σ’ αυτές τις δυνάμεις οφείλεται η πίεση που ασκεί το αέριο. Οι δυνάμεις αυτές είναι αντίθετες με τις δυνάμεις που ασκούνται από το τοίχωμα στα μόρια κατά την κρούση (αρχή δράσης- αντίδρασης) και προκαλούν τη μεταβολή της ορμής των μορίων.

Από το δεύτερο νόμο του Newton γνωρίζουμε ότι F =	ΔΡ	, άρα, αν καταφέρουμε να υπολογίσουμε

	Δt

τη συνολική μεταβολή της ορμής που υφίστανται τα μόρια στη μονάδα του χρόνου (δηλ. το ρυθμό μεταβολής της ορμής τους) λόγω των κρούσεών τους πάνω σε μία από τις έδρες του δοχείου θα βρούμε και το μέτρο της δύναμης που ασκείται από τα μόρια σ’ αυτή την έδρας.

Μετά, για να βρούμε την πίεση p, αρκεί να διαιρέσουμε τη δύναμη με την επιφάνεια

(Προσοχή : χρησιμοποιούμε κεφαλαίο P για την ορμή και μικρό p για την πίεση.)

Έστω ένα μόριο που κινείται με ταχύτητα υ₁. Αναλύουμε την ταχύτητά του σε τρεις συνιστώσες ( υ_1x , υ_1y , υ_1z ) (Σχ. 3.8). Εξετάζουμε τις κρούσεις στο τοίχωμα του δοχείου που είναι κάθετο στη υ_1x .

Εφόσον οι κρούσεις είναι απολύτως ελαστικές το μόριο ανακλάται με ταχύτητα ίδιου μέτρου. Η υ_1y και η υ_1z δε μεταβάλλονται ενώ η υ_1x αλλάζει φορά.

Η μεταβολή της ορμής που υφίσταται το μόριο κατά την κρούση θα είναι

ΔΡ_1x= -mυ_1x -mυ_1x = -2mυ_1x

Ο χρόνος που μεσολαβεί ανάμεσα σε δύο διαδοχικές κρούσεις του ίδιου σωματιδίου στην ίδια έδρα θα

είναι Δt =	2d	άρα ο αριθμός κρούσεων στη μονάδα του χρόνου για αυτό το μόριο στην ίδια έδρα θα

	υ_1x

είναι	υ_1x	και ο ρυθμός μεταβολής της ορμής του ( η μεταβολή της ορμής στη μονάδα του

	2d

χρόνου ) θα είναι	ΔΡ_1x	= -2mυ_1x	υ_1x	= -	mυ_1²x	.

	Δt		2d		d

Η δύναμη που δέχεται το μόριο από το τοίχωμα θα είναι F_1x=	ΔΡ_1x	= -	mυ_1²x	και αντίστοιχα αυτή

	Δt		d

που δέχεται το τοίχωμα από το μόριο θα είναι - F_1x=	mυ_1²x

	d

Η δύναμη (ΣFx) που ασκείται πάνω στο τοίχωμα που μελετάμε είναι το άθροισμα όλων των αντίστοιχων όρων που αφορούν κάθε μόριο χωριστά.

Η πίεση (p) που δέχεται η εν λόγω έδρα από το αέριο θα είναι p =	ΣF_x	όπου Α = d_²

	Α

Άρα

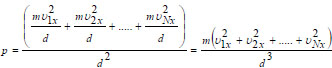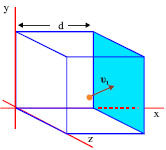Σχ. 3.7 Ένα μόριο του αερίου που κινείται με ταχύτητα υ1 μέσα σε κυβικό δοχείο ακμής d.

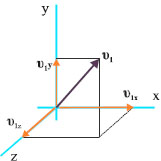Σχ. 3.8 Η ταχύτητα αναλύεται σε τρεις συνιστώσες σε τρισορθογώνιο σύστημα συντεταγμένων.

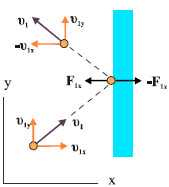Σχ. 3.9 Η κίνηση του μορίου στο επίπεδο xy.

Οι δυνάμεις που ασκούνται κατά τις κρούσεις των μορίων του αερίου, που περιέχουν τα μπαλόνια, με τα τοιχώματα τεντώνουν το ελαστικό περίβλημα των μπαλονιών.

Εικ. 3.3 Οι δυνάμεις που ασκούνται κατά τις κρούσεις των μορίων του αερίου, που περιέχουν τα μπαλόνια, με τα τοιχώματα τεντώνουν το ελαστικό περίβλημα των μπαλονιών.

Πολλαπλασιάζουμε και διαιρούμε το κλάσμα με Ν (το πλήθος των μορίων) οπότε

Ο όρος

είναι η μέση τιμή των τετραγώνων των υ_x ταχυτήτων και θα τον

συμβολίζουμε .

Τελικά

(3.10)

Τα μόρια κινούνται άτακτα, δεν έχουν δηλαδή καμιά προτίμηση ως προς την κατεύθυνση κίνησής τους, επομένως


Γνωρίζουμε ότι γενικά
Εύκολα αποδεικνύεται ότι
επειδή
καταλήγουμε στη σχέση

Αντικαθιστώντας το ίσον της στη σχέση (3.10) και λαμβάνοντας υπόψη ότι d³ =V προκύπτει

ΠΑΡΑΔΕΙΓΜΑ 3-4

Να βρεθεί η ενεργός ταχύτητα των μορίων του υδρογόνου σε θερμοκρασία 27^oC. Δίνεται ότι η γραμμομοριακή μάζα του υδρογόνου είναι 2x10^-3 kg/mol.

Απάντηση:

Γνωρίζουμε ότι

Πολλαπλασιάζοντας αριθμητή και παρονομαστή του υπόρριζου με τον αριθμό Avogadro (Ν_Α) προκύπτει

(3.11)

Όμως k =	R	επομένως kN_A = R και N_Am = M (Μ: η γραμμομοριακή μάζα)

	N_A

Άρα η σχέση (3.11) γίνεται
Αντικαθιστώντας στο SI		= 1,93x10³ m/s

Η ταχύτητα αυτή είναι πολύ μεγάλη, είναι περίπου 6900 km/h.