5.1 Εκθετική συνάρτηση Δυνάμεις με ρητό εκθέτη Σε προηγούμενες τάξεις γνωρίσαμε την έννοια της δύναμης με βάση έναν πραγματικό αριθμό και εκθέτη ακέραιο. Συγκεκριμένα: - Στην αρχή ορίσαμε τη δύναμη ενός πραγματικού αριθμού με εκθέτη θετικό ακέραιο, ως εξής: $α^ν = \begin{cases} \underbrace{α\cdot α\cdots \cdot α}_{v\text{ παράγοντες}} & ,αν\quad ν > 1\\ \quad \quad \quad \quad \quad \quad, α \in ℝ \quad και\quad ν \in \mathbb{N}^* \\ α & ,αν\quad ν = 1\end{cases} $ Για παράδειγμα: (- 12)3 = (- 12)(- 12)(- 12) = - 18 - Στη συνέχεια με τη βοήθεια των ισοτήτων: α0 = 1 και α-ν = 1αν = (1α)ν, α ≠ 0 και ν ∈ ℕ ∗ επεκτείναμε την έννοια της δύναμης ενός πραγματικού αριθμού και στην περίπτωση που ο εκθέτης είναι ακέραιος. Για παράδειγμα: (- 23)-2 = (- 32)2 = 94 Στη συνέχεια θα ορίσουμε παραστάσεις της μορφής 212, 514 και γενικά της μορφής αμν, όπου α ≥ 0, μ ακέραιος και ν θετικός ακέραιος. |
| Τις παραστάσεις αυτές θα ονομάσουμε δυνάμεις με ρητό εκθέτη. Ο ορισμός θα γίνει με τέτοιο τρόπο, ώστε να διατηρούνται οι γνωστές ιδιότητες των δυνάμεων. Τι θα πρέπει να σημαίνει π.χ. το 325; Αν απαιτήσουμε να ισχύει η ιδιότητα (αp)q = αpq και για τις δυνάμεις με ρητό εκθέτη, τότε θα είναι: (325)5 = 325·5 = 32 Άρα πρέπει ο 325 να είναι λύση της εξίσωσης x5 = 32, δηλαδή ο αριθμός $\sqrt[5]{3^2}$. Πρέπει δηλαδή να είναι $3^\frac{2}{5} = \sqrt[5]{3^2}$. Γενικά Αν α > 0, μ ακέραιος και ν θετικός ακέραιος, τότε ορίζουμε :
Επιπλέον, αν μ, ν, θετικοί ακέραιοι, ορίζουμε : 0μν = 0. Έτσι π.χ. $8^\frac{2}{3} = \sqrt[3]{8^2} = \sqrt[3]{64} = 4$ $27^{-\frac{4}{3}} = \sqrt[3]{27^{-4}} = \sqrt[3]{\dfrac{1}{27^4}} = \dfrac{1}{\sqrt[3]{27^4}} = \dfrac{1}{3^4}$ Αποδεικνύεται ότι, όλες οι ιδιότητες των δυνάμεων με εκθέτη ακέραιο ισχύουν και για τις δυνάμεις με εκθέτη ρητό. Το γεγονός αυτό διευκολύνει το λογισμό με τα ριζικά. Έτσι είναι π.χ. $\sqrt[4]{α} \cdot \sqrt[3]{α} = α^{\frac{1}{4}} \cdot α^{\frac{1}{3}} = α^{\frac{1}{4} + \frac{1}{3}} = α^\frac{7}{12} = \sqrt[12]{α^7}$ Οι δυνάμεις αυτές υπολογίζονται εύκολα με τη βοήθεια ενός υπολογιστή τσέπης ως εξής: ΔΥΝΑΜΗ 21,4 2 1,4-3,21 1.4 573 5 ΑΠΟΤΕΛΕΣΜΑ 2.6390158 0.3395697 42.749398 ΣΕΙΡΑ ΠΛΗΚΤΡΩΝ xy 1.4 = xy 3.21 +/- = xy ( 7 ÷ 3 ) = |
| Δυνάμεις με άρρητο εκθέτη Γεννιέται τώρα το ερώτημα: Μπορούμε να ορίσουμε δυνάμεις της μορφής αx με x άρρητο, κατά τέτοιο τρόπο ώστε να διατηρούνται οι βασικές ιδιότητες των δυνάμεων με ρητό εκθέτη; Μπορούμε για παράδειγμα να ορίσουμε την 3√2; Όπως είδαμε (βιβλίο Β' Γυμνασίου σελ. 104) οι δεκαδικές προσεγγίσεις του √2 κατά προσέγγιση ακέραιας μονάδας, δεκάτου, εκατοστού κτλ. είναι (1) 1, 1,4 , 1,41 , 1,414 , 1,4142 , 1,41421 , 1,414213, … Ας πάρουμε τώρα την ακολουθία αυτή των δεκαδικών προσεγγίσεων του √2 και την αντίστοιχη ακολουθία των δυνάμεων του 3: (2) 31 , 31,4 , 31,41 , 31,414 , 31,4142 , 31,41421 , 31,414213 , … Με τη βοήθεια ενός υπολογιστή τσέπης βρίσκουμε ότι: 31 = 3 31,4 $\simeq$ 4, 6555367 31,41 $\simeq$ 4,7 069650 31,414 $\simeq$ 4,72 76950 31,4142 $\simeq$ 4,728 7339 31,41421 $\simeq$ 4,728 7839 31,414213 $\simeq$ 4,7288 015 Αν παρατηρήσουμε τους αριθμούς αυτούς μας δίνεται η εξής εντύπωση: Όταν το πλήθος των δεκαδικών ψηφίων της ακολουθίας (1) αυξάνει, οι όροι της ακολουθίας (2) φαίνεται να προσεγγίζουν ένα ορισμένο αριθμό, που λέγεται οριακή τιμή ή όριο της ακολουθίας αυτής. Είναι επομένως λογικό να ορίσουμε τη δύναμη 3√2 ως την πιο πάνω οριακή τιμή. Έτσι με προσέγγιση τεσσάρων δεκαδικών ψηφίων είναι 3√2 $\cong$ 4,7288. Γενικά αποδεικνύεται ότι: Αν α > 0, x άρρητος και ρν η δεκαδική προσέγγιση του x με ν δεκαδικά ψηφία, τότε καθώς το ν αυξάνει τείνοντας στο +∞, οι όροι της ακολουθίας (αρν) «προσεγγίζουν» έναν ορισμένο πραγματικό αριθμό, τον οποίο στο εξής θα ονομάζουμε όριο της ακολουθίας (αρν). Το όριο αυτό συμβολίζεται με αx και λέγεται δύναμη του α με εκθέτη x. Συμβολικά γράφουμε: $α^x = \lim_{ν\to\infty}α^{ρ_ν}$ Επιπλέον, για κάθε x > 0, ορίζουμε 0x = 0. Ο υπολογισμός δυνάμεων με άρρητο εκθέτη γίνεται με υπολογιστή τσέπης όπως στα παρακάτω παραδείγματα: |
| ΔΥΝΑΜΗ 3√2 3 2π 2 ΑΠΟΤΕΛΕΣΜΑ 4.728801 8.824977 ΣΕΙΡΑ ΠΛΗΚΤΡΩΝ xy 2 √x = xy exp = Οι βασικές ιδιότητες των δυνάμεων, γνωστές από την Α′ Λυκείου, αποδεικνύεται ότι ισχύουν και για δυνάμεις με εκθέτη πραγματικό αριθμό. Συγκεκριμένα: Αν α, β είναι θετικοί πραγματικοί αριθμοί και x, x1, x2 ∈ ℝ, τότε: αx1 : αx2 = αx1− x2 αx1 · αx2 = αx1+x2 (αx1)x2 = αx1x2 (αβ)x = αxβx (α·β)x = αx · βx Εκθετική συνάρτηση Έστω α ένας θετικός αριθμός. Όπως είδαμε προηγουμένως για κάθε x ∈ ℝ ορίζεται η δύναμη αx. Επομένως αντιστοιχίζοντας κάθε x ∈ ℝ στη δύναμη αx, ορίζουμε τη συνάρτηση: f : ℝ → ℝ με f(x) = αx, η οποία, στην περίπτωση που είναι α ≠ 1, λέγεται εκθετική συνάρτηση με βάση α. Αν είναι α = 1, τότε έχουμε τη σταθερή συνάρτηση f(x) = 1. Έστω τώρα η εκθετική συνάρτηση f(x) = 2x. Για να σχεδιάσουμε τη γραφική της παράσταση κατασκευάζουμε τον πίνακα τιμών:
| |||||||||||||||||||||||||
| Τοποθετώντας τα σημεία (x, y) του παραπάνω πίνακα στο καρτεσιανό επίπεδο και ενώνοντάς τα με συνεχή καμπύλη έχουμε το διπλανό σχήμα. Η συνάρτηση αυτή, καθώς και κάθε συνάρτηση της μορφής f(x) = αx με α > 1, αποδεικνύεται ότι: |
| ||||||||||||||||||||||||
| ● Έχει πεδίο ορισμού το ℝ. ● Έχει σύνολο τιμών το διάστημα (0, +∞) των θετικών πραγματικών αριθμών. ● Είναι γνησίως αύξουσα στο ℝ. Δηλαδή για κάθε x1, x2 ∈ ℝ ισχύει: αν x1 < x2, τότε αx1 < αx2 ● Η γραφική της παράσταση τέμνει τον άξονα y′y στο σημείο Α(0,1) και έχει ασύμπτωτο τον αρνητικό ημιάξονα των x. | 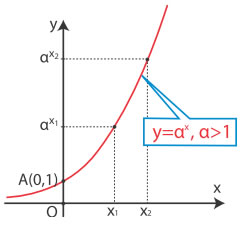 | ||||||||||||||||||||||||
| Έστω επιπλέον και η εκθετική συνάρτηση g(x) = (12)x. Για να σχεδιάσουμε τη γραφική της παράσταση κατασκευάζουμε τον πίνακα τιμών:
| |||||||||||||||||||||||||
| Τοποθετώντας τα σημεία (x, y) του παραπάνω πίνακα στο καρτεσιανό επίπεδο και ενώνοντάς τα με συνεχή καμπύλη έχουμε το διπλανό σχήμα. Η συνάρτηση αυτή, καθώς και κάθε συνάρτηση της μορφής f(x) = αx με 0 < α < 1, αποδεικνύεται ότι: ● Έχει πεδίο ορισμού το ℝ. ● Έχει σύνολο τιμών το διάστημα (0, +∞) των θετικών πραγματικών αριθμών. ● Είναι γνησίως φθίνουσα στο ℝ. Δηλαδή για κάθε x1, x2 ∈ ℝ ισχύει: αν x1 < x2, τότε αx1 > αx2 ● Η γραφική της παράσταση τέμνει τον άξονα y′y στο σημείο Α(0,1) και έχει ασύμπτωτο τον θετικό ημιάξονα των x. |
| ||||||||||||||||||||||||
| ΠΑΡΑΤΗΡΗΣΗ Για τις συναρτήσεις f(x) = 2x και g(x) = (12)x παρατηρούμε ότι για κάθε x ∈ R ισχύει: g(x) = (12)x = 12x = 2− x = f(-x) Αυτό σημαίνει ότι οι γραφικές παραστάσεις τους είναι συμμετρικές ως προς τον άξονα y′y. |
|
| ΣΧΟΛΙΟ Από τη μονοτονία της εκθετικής συνάρτησης f(x) = αx, με 0 < α ≠ 1, προκύπτει ότι: αν x1 ≠ x2 , τότε αx1 ≠ αx2 οπότε, με απαγωγή σε άτοπο, έχουμε ότι: αν αx1 = αx2 , τότε x1 = x2. Επομένως, ισχύει η ισοδυναμία: αx1 = αx2 ⇔ x1 = x2
Η ιδιότητα αυτή είναι ιδιαίτερα χρήσιμη για την επίλυση εξισώσεων, όπου ο άγνωστος εμφανίζεται στον εκθέτη. Οι εξισώσεις αυτές λέγονται εκθετικές εξισώσεις. | |
| ΠΑΡΑΔΕΙΓΜΑΤΑ 1º Να λυθούν οι εξισώσεις: i) 23x = 164 ii) 9x - 8·3x - 9 = 0 ΛΥΣΗ i) Η εξίσωση γράφεται διαδοχικά: 23x = 164 ⇔ 23x = 2− 6 [Επειδή η εκθετική συνάρτηση είναι 1-1] ⇔ 3x = -6 ⇔ x = -2 ii) Η εξίσωση γράφεται 32x - 8·3x - 9 = 0 ⇔ (3x)2 - 8·3x - 9 = 0 Αν θέσουμε 3x = y, αυτή γίνεται y2 - 8y - 9 = 0 και έχει ρίζες τους αριθμούς -1 και 9. Επομένως η αρχική εξίσωση έχει ως λύσεις τις λύσεις των εξισώσεων: 3x = -1 και 3x = 9 Απ' αυτές η πρώτη είναι αδύνατη, αφού 3x > 0, ενώ η δεύτερη γράφεται 3x = 32 και έχει ρίζα το x = 2, που είναι και μοναδική ρίζα της αρχικής εξίσωσης. 2º Να λυθεί το σύστημα: $\begin{cases} 2 \cdot 3^x - 3 \cdot 2^y = -22\\ 5 \cdot 3^x + \dfrac{1}{2} \cdot 2^y = 9 \end{cases} $ (εκθετικό σύστημα) ΛΥΣΗ Αν θέσουμε 3x = ω και 2y = φ το σύστημα γίνεται: $\begin{cases} 2ω - 3φ = -22\\ 5ω + \dfrac{1}{2}φ = 9\end{cases} $ Το γραμμικό αυτό σύστημα έχει λύση ω = 1 και φ = 8, οπότε το αρχικό σύστημα γράφεται: $\begin{cases} 3^x = 1\\ 2^y = 8 \end{cases} $ ή ισοδύναμα $\begin{cases} 3^x = 3^0\\ 2^y = 2^3 \end{cases} $ από το οποίο παίρνουμε x = 0 και y = 3. 3º Να λυθούν οι ανισώσεις: i) 3x2− 3x > 19 ii) (12)x2+x < 14 |
| ΛΥΣΗ i) Έχουμε 3x2-3x > 19 ⇔ 3x2− 3x > 3− 2 [αφού 3 > 1] ⇔ x2 - 3x > -2 ⇔ x2 - 3x + 2 > 0 ⇔ x < 1 ή x > 2 ii) Έχουμε (12)x2+x < 14 ⇔ (12)x2+x < (12)2 [αφού 12 < 1] ⇔ x2 + x > 2 ⇔ x2 + x - 2 > 0 ⇔ x < -2 ή x > 1 4º Να γίνουν οι γραφικές παραστάσεις των συναρτήσεων: i) f(x) = 2x + 3 ii) g(x) = 2x −3 iii) h(x) = 2x −3 + 2 ΛΥΣΗ | |
| i) Η γραφική παράσταση της f προκύπτει από μια κατακόρυφη μετατόπιση της φ(x) = 2x κατά 3 μονάδες προς τα πάνω. ii) Η γραφική παράσταση της g προκύπτει από μια οριζόντια μετατόπιση της φ(x) = 2x κατά 3 μονάδες προς τα δεξιά. iii) Τέλος η γραφική παράσταση της h προκύπτει από δυο μετατοπίσεις της φ(x) = 2x - μιας οριζόντιας κατά 3 μονάδες προς τα δεξιά και - μιας κατακόρυφης κατά 2 μονάδες προς τα πάνω. |
|
| |
| Ο αριθμός e Μια Τράπεζα για να διαφημιστεί κάνει μια πολύ ειδική προσφορά. Όποιος καταθέσει την επόμενη μέρα ποσό 1 εκατομμυρίου ευρώ, αυτό θα τοκιστεί με ετήσιο επιτόκιο 100% και με δυνατότητα ανατοκισμού του 1, 2, 3, … ή ν φορές το χρόνο, σε ίσα χρονικά διαστήματα, ανάλογα με την επιθυμία του καταθέτη. Έχει σημασία για τον καταθέτη το πόσες φορές το χρόνο θα ανατοκιστεί το κεφάλαιο: Από το γνωστό τύπο του ανατοκισμού αν = α0(1 + τ)ν, όπου τ = ε 100. ● αν ν = 1, είναι τ = 1 και α1 = 1·(1 + 1)1 = 2 εκατομμύρια ευρώ. ● αν ν = 2, είναι τ = 12 και α2 = 1·(1 + 12)2 = 2,25 εκατομμύρια ευρώ. ● αν ν = 3, είναι τ = 13 και α3 = 1·(1 + 13)3 = 2,44 εκατομμύρια ευρώ. ………………………………………………………………………………… ● αν ν = ν, είναι τ = 1ν και αν = 1·(1 + 1ν)ν = (1 + 1ν)ν εκατομμύρια ευρώ. Αν χρησιμοποιήσουμε υπολογιστή τσέπης κατασκευάζουμε τον πίνακα:
Παρατηρούμε ότι, καθώς το ν αυξάνει, αυξάνει και το (1 + 1ν)ν και προσεγγίζει έναν ορισμένο πραγματικό αριθμό. Ο αριθμός αυτός είναι άρρητος και συμβολίζεται με e. Ο συμβολισμός αυτός οφείλεται στο μεγάλο Ελβετό, μαθηματικό Leohard Euler (1707-1783). Ο αριθμός e με προσέγγιση πέντε δεκαδικών ψηφίων είναι e = 2,71828. Συμβολικά γράφουμε
Από τα παραπάνω βλέπουμε ότι οι τιμές του ν έχουν μεγάλη σημασία όσο αυτές παραμένουν «μικρές». Από μια τιμή όμως και μετά, όσο και αν αυξάνει το ν, το τελικό ποσό δεν μεταβάλλεται ουσιαστικά. |
Σε πολλές πραγματικές εφαρμογές εμφανίζονται εκθετικές συναρτήσεις με βάση τον αριθμό e. Η απλούστερη τέτοια συνάρτηση είναι η f(x) = ex. Η συνάρτηση αυτή ονομάζεται απλώς εκθετική και η γραφική της παράσταση φαίνεται στο διπλανό σχήμα. |
|
| Ο νόμος της εκθετικής μεταβολής Μία ακόμη εκθετική συνάρτηση με βάση το e είναι η (1) Q(t) = Q0·ect Αυτή εκφράζει ένα φυσικό μέγεθος, που μεταβάλλεται με το χρόνο t. To Q0 είναι η αρχική τιμή του Q (για t = 0) και είναι Q0 > 0, ενώ το c είναι μια σταθερά που εξαρτάται κάθε φορά από τη συγκεκριμένη εφαρμογή. Η συνάρτηση αυτή είναι γνωστή ως νόμος της εκθετικής μεταβολής. Αν c > 0 η συνάρτηση Q είναι γνησίως αύξουσα και εκφράζει το νόμο της εκθετικής αύξησης, ενώ αν c < 0 η Q είναι γνησίως φθίνουσα και εκφράζει το νόμο της εκθετικής απόσβεσης. Ο νόμος της εκθετικής μεταβολής αποτελεί ένα ικανοποιητικό μοντέλο για πάρα πολλές εφαρμογές της Φυσικής, της Βιολογίας, της Στατιστικής και άλλων επιστημών. Για παράδειγμα ο αριθμός των γραμμαρίων μιας ραδιενεργού ουσίας κατά τη χρονική στιγμή t (σε δευτερόλεπτα) δίνεται από τον τύπο Q(t) = 200·e− 0,3t. Αυτό σημαίνει ότι η ουσία που παραμένει αδιάσπαστη μετά από 7 δευτερόλεπτα είναι: Q(7) = 200e− 0,3·7 $\simeq$ 200(2,718)− 2,1 $\simeq$ 24,5 γραμμάρια. Ο χρόνος που χρειάζεται για να διασπασθεί ή να εξαφανισθεί η μισή ποσότητα μιας ραδιενεργού ουσίας λέγεται ημιζωή ή χρόνος υποδιπλασιασμού της ραδιενεργού ουσίας. Στον πίνακα που ακολουθεί αναφέρεται η ημιζωή ορισμένων ραδιενεργών ισοτόπων: ΙΣΟΤΟΠΟ Άνθρακας (C14) Ράδιο (Ra226) Πολώνιο (Ρο210) Φώσφορος (Ρ32) ΗΜΙΖΩΗ 5730 έτη 1600 έτη 138 ημέρες 14 ημέρες | |
| ΠΑΡΑΔΕΙΓΜΑ Αν η ημιζωή ενός ραδιενεργού υλικού είναι 5 χρόνια, να αποδειχθεί ότι η συνάρτηση που εκφράζει την εκθετική απόσβεση αυτού είναι Q(t) = Q02 −t/5. ΑΠΟΔΕΙΞΗ Αφού η ημιζωή είναι 5 χρόνια, από το νόμο της εκθετικής απόσβεσης Q(t) = Q0·ect έχουμε: Q02 = Q0·ect ⇔ e5c = 12 ⇔ $e^c = \sqrt[5]{\dfrac{1}{2}} = 2^{-\frac{1}{5}}$ Άρα Q(t) = Q02− t/5 ΑΣΚΗΣΕΙΣ
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||
| ||||||