3.3 ΑΝΑΓΩΓΗ ΣΤΟ 1o ΤΕΤΑΡΤΗΜΟΡΙΟ

3.3 ΑΝΑΓΩΓΗ ΣΤΟ 1^o ΤΕΤΑΡΤΗΜΟΡΙΟ

Ο υπολογισμός των τριγωνομετρικών αριθμών οποιασδήποτε γωνίας μπορεί να γίνει, όπως θα δούμε στη συνέχεια, με τη βοήθεια πινάκων που δίνουν τους τριγωνομετρικούς αριθμούς γωνιών από 0^o μέχρι 90^o. Ας θεωρήσουμε δύο γωνίες ω και ω' που οι τελικές πλευρές τους τέμνουν τον τριγωνομετρικό κύκλο στα σημεία Μ και Μ' αντιστοίχως.

Γωνίες αντίθετες

Αν οι γωνίες ω και ω' είναι αντίθετες, δηλαδή αν ω' = −ω, τότε, όπως φαίνεται στο διπλανό σχήμα, τα σημεία Μ και Μ΄ είναι συμμετρικά ως προς τον άξονα x'x. Επομένως τα σημεία αυτά έχουν την ίδια τετμημένη και αντίθετες τεταγμένες. Έχοντας υπόψη τους ορισμούς των τριγωνομετρικών αριθμών, συμπεραίνουμε ότι :

συν (−ω) = συνω ηµ (−ω) = −ηµω
εϕ (−ω) = −εϕω σϕ (−ω) = −σϕω

Δηλαδή :
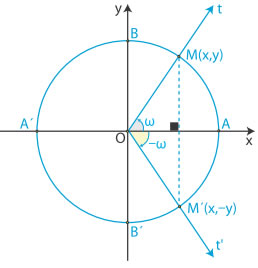οι αντίθετες γωνίες έχουν το ίδιο συνημίτονο και αντίθετους τους άλλους τριγωνομετρικούς αριθμούς.

Για παράδειγμα :

✔ Έχουμε :

$ηµ(-30^\circ) = -ημ(30^\circ) = -\dfrac{1}{2}$	$συν(-30^\circ) = συν(30^\circ) = \dfrac{\sqrt{3}}{2}$
$εφ(-30^\circ) = -εφ(30^\circ) = -\dfrac{\sqrt{3}}{3}$	$σφ(-30^\circ) = -σφ(30^\circ) = -\sqrt{3}$

✔ Επίσης, έχουμε :

$ηµ\left(-\dfrac{π}{4}\right) = -ημ\dfrac{π}{4} = -\dfrac{\sqrt{2}}{2}$	$συν\left(-\dfrac{π}{4}\right) = συν\dfrac{π}{4} = \dfrac{\sqrt{2}}{2}$

$εφ\left(-\dfrac{π}{4}\right) = -εφ\dfrac{π}{4} = -1$	$σφ\left(-\dfrac{π}{4}\right) = -σφ\dfrac{π}{4} = -1 $

Μικροπείραμα

Γωνίες με άθροισμα 180$^\circ$

Αν οι γωνίες ω και ω' έχουν άθροισμα 180^o , δηλαδή αν ω' = 180^o− ω , τότε, όπως φαίνεται στο διπλανό σχήμα, τα σημεία Μ και Μ' είναι συμμετρικά ως προς τον άξονα y'y . Επομένως τα σημεία αυτά έχουν την ίδια τεταγμένη και αντίθετες τετμημένες. Έχοντας υπόψη τους ορισμούς των τριγωνομετρικών αριθμών, συμπεραίνουμε ότι :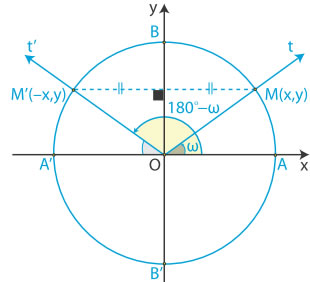

ημ(180^o− ω) = ημω συν (180^o− ω) = −συνω
εφ (180^o− ω) = −εϕω σϕ (180^o− ω) = −σϕω

Δηλαδή :

Οι γωνίες με άθροισμα 180$^\circ$ έχουν το ίδιο ημίτονο και αντίθετους τους άλλους τριγωνομετρικούς αριθμούς.

Για παράδειγμα :

✔ Επειδή 150$^\circ$ = 180$^\circ$ - 30$^\circ$ , έχουμε:

$ημ150^\circ = ημ(180^\circ - 30^\circ) = ημ30^\circ = \dfrac{1}{2}$

$συν150^\circ = συν(180^\circ - 30^\circ) = -συν30^\circ = -\dfrac{\sqrt{3}}{2}$

$εφ150^\circ = εφ(180^\circ - 30^\circ) = -εφ30^\circ = -\dfrac{\sqrt{3}}{3}$

$σφ150^\circ = σφ(180^\circ - 30^\circ) = -σφ30^\circ = -\sqrt{3}$

✔ Επειδή $\dfrac{2π}{3} = π - \dfrac{π}{3}$ , έχουμε:

$ημ\left(\dfrac{2π}{3}\right) = ημ\left(π - \dfrac{π}{3}\right) = ημ\dfrac{π}{3} = \dfrac{\sqrt{3}}{2}$

$συν\left(\dfrac{2π}{3}\right) = συν\left(π - \dfrac{π}{3}\right) = -συν\dfrac{π}{3} = -\dfrac{1}{2}$

$εφ\left(\dfrac{2π}{3}\right) = εφ\left(π - \dfrac{π}{3}\right) = -εφ\dfrac{π}{3} = -\sqrt{3}$

$σφ\left(\dfrac{2π}{3}\right) = σφ\left(π - \dfrac{π}{3}\right) = -σφ\dfrac{π}{3} = -\dfrac{\sqrt{3}}{3}$

Μικροπείραμα

Γωνίες που διαφέρουν κατά 180$^\circ$
Αν οι γωνίες ω και ω' διαφέρουν κατά 180$^\circ$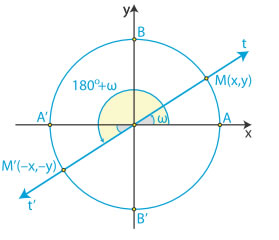, δηλαδή αν ω' = 180$^\circ$ + ω , τότε, όπως φαίνεται στο διπλανό σχήμα, τα σημεία Μ και Μ' είναι συμμετρικά ως προς την αρχή των αξόνων. Επομένως τα σημεία αυτά έχουν αντίθετες τετμημένες και αντίθετες τεταγμένες. Έχοντας υπόψη τους ορισμούς των τριγωνομετρικών αριθμών, συμπεραίνουμε ότι :

ημ(180$^\circ$ + ω) = −ημω συν (180$^\circ$ + ω) = −συνω
εφ (180$^\circ$+ ω) = εϕω σϕ (180$^\circ$ + ω) = σϕω

Δηλαδή :

Οι γωνίες που διαφέρουν κατά 180$^\circ$ έχουν αντίθετο ημίτονο και συνημίτονο, ενώ έχουν την ίδια εφαπτομένη και συνεφαπτομένη.

Για παράδειγμα :

✔ Επειδή 210$^\circ$ = 180$^\circ$ + 30$^\circ$ , έχουμε:

$ημ210^\circ = ημ(180^\circ + 30^\circ) = -ημ30^\circ = -\dfrac{1}{2}$

$συν210^\circ = συν(180^\circ + 30^\circ) = -συν30^\circ = -\dfrac{\sqrt{3}}{2}$

$εφ210^\circ = εφ(180^\circ + 30^\circ) = εφ30^\circ = \dfrac{\sqrt{3}}{3}$

$σφ210^\circ = σφ(180^\circ + 30^\circ) = σφ30^\circ = \sqrt{3}$

✔ Επειδή $\dfrac{4π}{3} = π + \dfrac{π}{3}$ , έχουμε:

$ημ\left(\dfrac{4π}{3}\right) = ημ\left(π + \dfrac{π}{3}\right) = -ημ\dfrac{π}{3} = -\dfrac{\sqrt{3}}{2}$

$συν\left(\dfrac{4π}{3}\right) = συν\left(π + \dfrac{π}{3}\right) = -συν\dfrac{π}{3} = -\dfrac{1}{2}$

$εφ\left(\dfrac{4π}{3}\right) = εφ\left(π + \dfrac{π}{3}\right) = εφ\dfrac{π}{3} = \sqrt{3}$

$σφ\left(\dfrac{4π}{3}\right) = σφ\left(π + \dfrac{π}{3}\right) = σφ\dfrac{π}{3} = \dfrac{\sqrt{3}}{3}$

Μικροπείραμα

Γωνίες με άθροισμα 90$^\circ$

Αν οι γωνίες ω και ω' έχουν άθροισμα 90$^\circ$,δηλαδή ω' = 90$^\circ$ − ω, τότε, όπως φαίνεται στο διπλανό σχήμα, τα
σημεία Μ και Μ' είναι συμμετρικά ως προς τη διχοτόμο της γωνίας xOy . Επομένως η τετμημένη του καθενός ισούται με την τεταγμένη του άλλου. Έχοντας υπόψη τους ορισμούς των τριγωνομετρικών αριθμών, συμπεραίνουμε ότι :

ημ(90$^\circ$ − ω) = συνω συν (90$^\circ$ − ω) = ημω
εφ (90$^\circ$− ω) = σϕω σϕ (90$^\circ$ − ω) = εϕω

Δηλαδή,

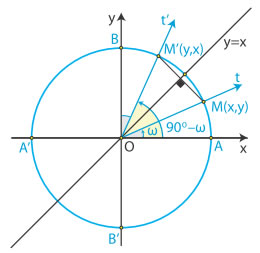Αν δύο γωνίες έχουν άθροισμα 90$^\circ$ , τότε το ημίτονο της μιας ισούται με το συνημίτονο της άλλης και η εφαπτομένη της μιας ισούται με τη συνεφαπτομένη της άλλης.

Για παράδειγμα, επειδή 60$^\circ$= 90$^\circ$ −30$^\circ$, έχουμε :

$ημ60^\circ = συν30^\circ = \dfrac{\sqrt{3}}{2}$ ,		$συν60^\circ = ημ30^\circ = \dfrac{1}{2}$ ,

$εφ60^\circ = σφ30^\circ = \sqrt{3}$	και	$σφ60^\circ = εφ30^\circ = \dfrac{\sqrt{3}}{3}$

Μικροπείραμα

ΣΧΟΛΙΟ

Από τα προηγούμενα καταλαβαίνουμε ότι δεν χρειάζεται να έχουμε πίνακες τριγωνομετρικών αριθμών όλων των γωνιών, αλλά μόνο των γωνιών από 0$^\circ$ μέχρι 90$^\circ$.

ΕΦΑΡΜΟΓΕΣ

1^η Δίνεται ότι $συν36^\circ = \dfrac{1+\sqrt{5}}{4}$ . Να υπολογιστούν οι τριγωνομετρικοί αριθμοί της γωνίας 54$^\circ$.

ΛΥΣΗ

Επειδή 54$^\circ$ = 90$^\circ$ - 36$^\circ$, έχουμε

$ημ54^\circ = συν36^\circ = \dfrac{1 + \sqrt{5}}{4}$

Σύμφωνα με την ταυτότητα $ηµ^2ω + συν^2ω = 1 $ ισχύει

$ηµ^254^\circ + συν^254^\circ = 1 $, οπότε:

$συν^254^\circ = 1 - ηµ^254^\circ = 1 - \left(\dfrac{1+\sqrt{5}}{4}\right)^2 = 1 - \dfrac{6 + 2\sqrt{5}}{16} = \dfrac{10 - 2\sqrt{5}}{16}$ ,

οπότε:

$συν54^\circ = \dfrac{\sqrt{10 - 2\sqrt{5}}}{4}$

Επομένως είναι:

$εφ54^\circ = \dfrac{ημ54^\circ}{συν54^\circ} = \dfrac{1 + \sqrt{5}}{\sqrt{10 - 2\sqrt{5}}} \quad \quad $ και $\quad \quad σφ54^\circ = \dfrac{συν54^\circ}{ημ54^\circ} = \dfrac{\sqrt{10 - 2\sqrt{5}}}{1 + \sqrt{5}} .$

2^η Να υπολογιστούν με τη βοήθεια της γωνίας ω οι τριγωνομετρικοί αριθμοί των γωνιών :

α) 90$^\circ$+ ω β) 270$^\circ$ − ω και γ) 270$^\circ$ + ω

ΛΥΣΗ

i) Επειδή 90$^\circ$+ ω = 90$^\circ$ − (−ω) έχουμε :

ηµ(90$^\circ$+ ω) = ηµ(90$^\circ$ − (−ω)) = συν (−ω) = συνω .

Ομοίως υπολογίζονται οι υπόλοιποι τριγωνομετρικοί αριθμοί της γωνίας 90$^\circ$ + ω .

ii) Επειδή 270$^\circ$− ω = 180$^\circ$ + (90$^\circ$ −ω) έχουμε :

ηµ(270$^\circ$ − ω) = ηµ(180$^\circ$ + (90$^\circ$−ω)) = −ημ(90$^\circ$ − ω) = −συνω .

Ομοίως υπολογίζονται οι υπόλοιποι τριγωνομετρικοί αριθμοί της γωνίας 270$^\circ$ − ω.

iii) Επειδή 270$^\circ$+ ω = 360$^\circ$ − 90$^\circ$ + ω = 360$^\circ$ + (ω − 90$^\circ$), έχουμε :

εφ(270$^\circ$ + ω) = εφ(ω − 90$^\circ$) = −εφ(90$^\circ$ − ω) = −σφω .

Ομοίως υπολογίζονται οι υπόλοιποι τριγωνομετρικοί αριθμοί της γωνίας 270$^\circ$ + ω.

ΑΣΚΗΣΕΙΣ

Α′ ΟΜΑΔΑΣ

1. Να βρείτε τους τριγωνομετρικούς αριθμούς της γωνίας :

i) 1200$^\circ$ ii) -2850$^\circ$

Μικροπείραμα Μικροπείραμα

2. Να βρείτε τους τριγωνομετρικούς αριθμούς της γωνίας

i)$\dfrac{187π}{6}$ rad ii) $\dfrac{21π}{4}$ rad

Μικροπείραμα

3. Σε κάθε τρίγωνο ΑΒΓ να αποδείξετε ότι :

i) ηµΑ = ημ(Β + Γ)		ii) συνΑ + συν(Β + Γ) = 0

iii) $ημ\dfrac{A}{2} = συν\dfrac{B + Γ}{2}$		iv) $συν\dfrac{A}{2} = ημ\dfrac{B + Γ}{2}$ .

4. Να απλοποιήσετε την παράσταση $\dfrac{συν(-α) \cdot συν(180^\circ + α)}{ημ(-α) \cdot ημ(90^\circ + α)}$ .

5. Να αποδείξετε ότι : $\dfrac{εφ(π - x) \cdot συν(2π + x) \cdot συν \left(\dfrac{9π}{2} + x \right)}{ημ(13π + x) \cdot συν(- x) \cdot σφ \left(\dfrac{21π}{2} - x \right)} = -1.$

6. Να δείξετε ότι έχει σταθερή τιμή η παράσταση :

$ημ^2(π - x) + συν(π - x)συν(2π - x) + 2ημ^2\left(\dfrac{π}{2} - x\right)$ .

B′ ΟΜΑΔΑΣ

1. Να υπολογίσετε την τιμή της παράστασης :

$\dfrac{ημ495^\circ \cdot συν120^\circ + συν495^\circ \cdot συν(-120^\circ)}{εφ(-120^\circ) + εφ495^\circ}$ .

2. Να αποδείξετε ότι :

$\dfrac{ημ(5π + ω) \cdot συν(7π - ω) \cdot ημ\left(\dfrac{5π}{2} - ω\right) \cdot συν\left(\dfrac{7π}{2} + ω\right)}{σφ(5π + ω) \cdot ημ(7π - ω) \cdot συν\left(\dfrac{5π}{2} - ω\right) \cdot σφ\left(\dfrac{7π}{2} + ω\right)} = ημ^2ω - 1$ .

3. Αν $εφ\left(\dfrac{π}{3} - x\right) + εφ\left(\dfrac{π}{6} + x\right) = 5$, να υπολογίσετε την τιμή της παράστασης :

$εφ^2\left(\dfrac{π}{3} - x\right) + εφ^2\left(\dfrac{π}{6} + x\right)$ .

4. Να αποδείξετε ότι :

$0 < \dfrac{εφ(π + x)}{εφx + σφ(π+x)} < 1 .$

Μικροπείραμα

ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ

I) Σε καθεμιά από τις παρακάτω περιπτώσεις να κυκλώσετε το γράμμα Α, αν ο ισχυρισμός είναι αληθής και το γράμμα Ψ, αν ο ισχυρισμός είναι ψευδής.
1. Αν ημω =1, τότε υποχρεωτικά θα είναι συνω= 0 .	A	Ψ
2. Αν συνω= 0 , τότε υποχρεωτικά θα είναι ημω= 1.	A	Ψ
3. Υπάρχει γωνία ω με ημω + συνω =2 .	A	Ψ
4. Για κάθε γωνία ω ισχύει $ημω = \sqrt{1 - συν^2ω}$	A	Ψ
5. ημ²20$^\circ$ + ημ²70$^\circ$ = 1	A	Ψ
6. Για κάθε x ∈ ℝ ισχύει ηµ(x − π) = −ηµx	A	Ψ
7. Για κάθε x ∈ ℝ ισχύει ημ²x = ημx²	A	Ψ
8. Αν $συν\left(x - \dfrac{π}{2}\right) + ημx = 0$ , τότε ηµx = 0	A	Ψ
9. Για κάθε x ∈ ℝ ισχύει	A	Ψ

II. Να αντιστοιχίσετε καθένα από τους τριγωνομετρικούς αριθμούς της Α΄ ομάδας με τον ίσο του από τη Β΄ ομάδα.

Εικόνα

III. Σε καθεμιά από τις παρακάτω περιπτώσεις να επιλέξετε τη σωστή απάντηση.

1. Αν ένα τρίγωνο ΑΒΓ είναι ορθογώνιο ( Α =90$^\circ$) και όχι ισοσκελές, τότε :

Α) ηµ²Β + ηµ²Γ = 1, Β) ηµ²Β + συν²Γ = 1, Γ) εφΒ=1.

2. Αν ένα τρίγωνο ΑΒΓ δεν είναι ορθογώνιο τότε :

Α) συν(Β + Γ) = συνΑ , Β) ημ(Β + Γ) = ημΑ , Γ) εφ(Β + Γ) = εφΑ .

3. Αν ένα τρίγωνο ΑΒΓ δεν είναι ορθογώνιο τότε :

A) $συν\left(\dfrac{B + Γ}{2}\right) = ημ\dfrac{Α}{2}$ , Β) $συν\left(\dfrac{B + Γ}{2}\right) = συν\dfrac{Α}{2}$ , Γ) $εφ\left(\dfrac{B + Γ}{2}\right) = εφ\dfrac{Α}{2}$ .