1.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Η εξίσωση αx + βy = γ Στο Γυμνάσιο διαπιστώσαμε με τη βοήθεια παραδειγμάτων ότι η εξίσωση αx + βy = γ, με α ≠ 0 ή β ≠ 0 , που λέγεται γραμμική εξίσωση, παριστάνει ευθεία γραμμή. Στη συνέχεια θα αποδείξουμε το συμπέρασμα αυτό ως εξής : Διακρίνουμε δύο περιπτώσεις : • Αν , β ≠ 0 , τότε η εξίσωση γράφεται : αx + βy = γ ⇔ βy = -αx + γ Επομένως η εξίσωση αυτή παριστάνει ευθεία που έχει συντελεστή διεύθυνσης λ = -$\dfrac{α}{β}$ και τέμνει τον άξονα y'y στο σημείο $\dfrac{γ}{β}$ .
Ειδικότερα : |
| ✔ Αν α = 0 , τότε η εξίσωση παίρνει τη μορφή y = $\dfrac{γ}{β}$ και επομένως παριστάνει ευθεία που είναι παράλληλη στον άξονα x'x και τέμνει τον άξονα y'y στο σημείο $\dfrac{γ}{β}$(Σχ. β΄).
| |
• Αν β = 0 (οπότε α ≠ 0), τότε η εξίσωση γράφεται αx = γ ⇔ x = $\dfrac{γ}{α}$ Επομένως η εξίσωση αυτή παριστάνει ευθεία που είναι παράλληλη στον άξονα y'y και τέμνει τον άξονα x'x στο σημείο $\dfrac{γ}{α}$ . Για παράδειγμα : | 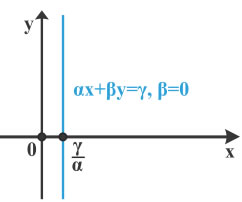 |
| ✔ Η εξίσωση x − 2y = 2 παίρνει τη μορφή y = $\dfrac{1}{2}$x − 1 η οποία παριστάνει ευθεία που έχει συντελεστή διεύθυνσης λ = $\dfrac{1}{2}$ και τέμνει τον άξονα y'y στο σημείο −1 . | 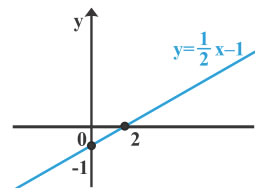 |
| ✔ Η εξίσωση y=2 παριστάνει ευθεία που είναι παράλληλη στον άξονα x'x και τέμνει τον άξονα y'y στο σημείο 2 . | 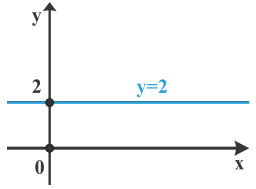 |
| ✔ Η εξίσωση x=2 παριστάνει ευθεία που είναι παράλληλη στον άξονα y'y και τέμνει τον άξονα x'x στο σημείο 2. | 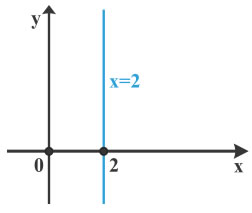 |
| Κάθε ζεύγος αριθμών που επαληθεύει μία γραμμική εξίσωση λέγεται λύση της γραμμικής εξίσωσης.
Για παράδειγμα, το ζεύγος (4,-1) είναι λύση της εξίσωσης x − 2y = 6, αφού 4 − 2(−1) = 4 + 2 = 6. Διαπιστώνουμε, όμως, ότι και τα ζεύγη (16,5), (−10, −8) είναι λύσεις της εξίσωσης και γενικά ότι κάθε ζεύγος της μορφής (k, $\dfrac{1}{2}$k−3), k ∈ ℝ είναι λύση της εξίσωσης. Γραμμικό σύστημα 2 x 2
Κάθε ζεύγος αριθμών που επαληθεύει και τις δύο εξισώσεις του συστήματος λέγεται λύση του συστήματος. • Λύνουμε τη μια εξίσωση του συστήματος ως προς έναν άγνωστο και τον αντικαθιστούμε στην άλλη εξίσωση. • Αντικαθιστούμε μια από τις εξισώσεις (ε) ή (ε') του συστήματος, π.χ. την (ε), με την εξίσωση « λ(ε) + λ'(ε') » που προκύπτει, αν στα μέλη της (ε) πολλαπλασιασμένα με λ≠0, προσθέσουμε τα μέλη της (ε') πολλαπλασιασμένα με λ'. Η εξίσωση λ(ε) + λ'(ε') λέγεται γραμμικός συνδυασμός των εξισώσεων (ε) και (ε'). Η απόδειξη του ότι τα συστήματα που προκύπτουν από τις παραπάνω μετατροπές είναι ισοδύναμα στηρίζεται στις παρακάτω ιδιότητες της ισότητας που είδαμε στο 2o κεφάλαιο του βιβλίου της Α´ Λυκείου: ✔ Αν γ ≠ 0, τότε: α = β ⇔ αγ = βγ Έστω, για παράδειγμα, ότι θέλουμε να λύσουμε το σύστημα : $$\begin{cases}x - 2y = 6 \quad \quad (1) \\ 3x + 4y = 8 \quad \quad (2) \end{cases}$$ |
Θα λύσουμε το σύστημα με τις δύο μεθόδους που μάθαμε στο Γυμνάσιο, τη μέθοδο της αντικατάστασης και τη μέθοδο των αντιθέτων συντελεστών (ή μέθοδο της απαλοιφής) Μέθοδος της αντικατάστασης
$$\begin{cases}x = 2y + 6 \\ 3x + 4y = 8 \end{cases}$$ Αντικαθιστούμε στη δεύτερη εξίσωση το x με την παράσταση που βρήκαμε και λύνουμε την εξίσωση που προκύπτει 3(2y + 6) + 4y = 8 ⇔ 6y + 18 + 4y = 8 Έτσι το σύστημα είναι ισοδύναμο με το $$\begin{cases}x = 2y + 6 \\ y = -1 \end{cases}$$ Αντικαθιστούμε την τιμή του y στην πρώτη εξίσωση και υπολογίζουμε τον άλλο άγνωστο : x = 2(−1) + 6 = 4 Άρα λύση του συστήματος είναι το ζεύγος (4, −1). ΣΧΟΛΙΟ Επειδή κάνουμε πολλά βήματα μέχρι να λύσουμε ένα σύστημα, είναι πολύ πιθανό να κάνουμε λάθος στους αριθμητικούς υπολογισμούς. Για το λόγο αυτό είναι σκόπιμο να αντικαθιστούμε τις τιμές των αγνώστων που βρήκαμε στις αρχικές εξισώσεις του συστήματος και να ελέγχουμε αν τις επαληθεύουν, δηλαδή να κάνουμε επαλήθευση του συστήματος. Στο συγκεκριμένο σύστημα, για x = 4 και y = −1, έχουμε :
Μέθοδος των αντίθετων συντελεστών (ή της απαλοιφής) Πολλαπλασιάζουμε τα μέλη των δύο εξισώσεων με κατάλληλους αριθμούς, ώστε οι συντελεστές του ενός αγνώστου στις εξισώσεις που θα προκύψουν να είναι αντίθετοι : |
$$\begin{cases} \begin{array}{c|c} x - 2y = 6 & ⋅ (-3) \\ 3x + 4y = 8 & ⋅ 1 \end{array} \end{cases} $$ ή ισοδύναμα $$\begin{cases} -3x + 6y = -18 \\ 3x + 4y = 8 \end{cases} $$ | |||||
Προσθέτουμε κατά μέλη τις εξισώσεις που βρήκαμε, οπότε προκύπτει εξίσωση με έναν άγνωστο, την οποία και επιλύουμε : − 3x + 6y + 3x + 4y = -18 + 8 ⇔ 10y = -10 ⇔ y = -1 . Αντικαθιστούμε την τιμή του αγνώστου που βρήκαμε σε μια από τις αρχικές εξισώσεις και βρίσκουμε την τιμή του άλλου : x - 2(-1) = 6 ⇔ x + 2 = 6 ⇔ x = 4 . Άρα η λύση του συστήματος είναι το ζεύγος (4, −1) (η ίδια φυσικά που βρέθηκε και με την προηγούμενη μέθοδο). Γραφική επίλυση γραμμικού συστήματος 2 x 2 Κάθε εξίσωση του γραμμικού συστήματος $$\begin{cases}x - 2y = 6 \\ 3x + 4y = 8 \end{cases}$$ που λύσαμε προηγουμένως παριστάνει μια ευθεία γραμμή. Το σημείο τομής των ευθειών αυτών προσδιορίζει τη λύση του συστήματος, αφού οι συντεταγμένες του επαληθεύουν συγχρόνως τις δύο εξισώσεις του συστήματος.
Γενικά, μπορούμε να επιλύσουμε γραφικά ένα γραμμικό σύστημα $$\begin{cases} αx + βy = γ \\ α'x + β'y = γ ' \end{cases}$$ με το να σχεδιάσουμε τις δύο ευθείες που παριστάνουν οι εξισώσεις του και να βρούμε, εφόσον υπάρχει, το σημείο τομής τους. | |||||
Οι δύο εξισώσεις ενός γραμμικού συστήματος 2 x 2 παριστάνουν δύο ευθείες οι οποίες μπορεί να τέμνονται ή να είναι παράλληλες ή ακόμα και να συμπίπτουν. Για παράδειγμα : ✔ Το σύστημα $$\begin{cases} 2x + 3y = 3 \\ 4x - 9y = 1 \end{cases}$$ γράφεται $$\begin{cases} y = - \dfrac{2}{3}x + 1 \\ y = \dfrac{4}{9}x - \dfrac{1}{9} \end{cases}$$ και έχει μοναδική λύση , αφού οι δύο ευθείες που παριστάνουν οι εξισώσεις του τέμνονται, επειδή έχουν διαφορετικούς συντελεστές διεύθυνσης. | |||||
Αν χαράξουμε τις ευθείες που παριστάνουν Αν όμως λύσουμε το σύστημα αλγεβρικά, θα βρούμε ότι η ακριβής λύση του συστήματος είναι το ζεύγος (1, $\frac{1}{3}$) | 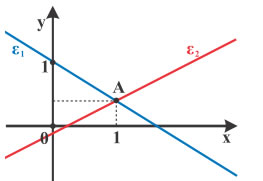 | ||||
✔ Το σύστημα $$\begin{cases} x + 2y = 3 \\ 2x + 4y = -5 \end{cases}$$ γράφεται $$\begin{cases} y = - \dfrac{1}{2}x + \dfrac{3}{2} \\ y = - \dfrac{1}{2}x - \dfrac{5}{4} \end{cases}$$ οπότε είναι αδύνατο, αφού οι δύο ευθείες που παριστάνουν οι εξισώσεις του είναι παράλληλες. | 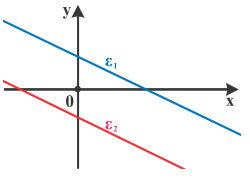 | ||||
| ✔ Το σύστημα $$\begin{cases} y + 1 = 2x \\ 4x - 2y = 2 \end{cases}$$ γράφεται $$\begin{cases} y = 2x - 1 \\ y = 2x - 1 \end{cases}$$ οπότε έχει άπειρο πλήθος λύσεων, αφού οι δύο ευθείες που παριστάνουν οι εξισώσεις του συστήματος συμπίπτουν. | 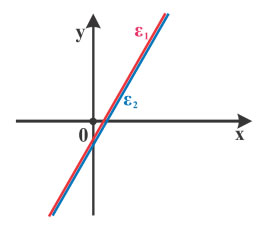 | ||||
Προφανώς κάθε λύση του συστήματος είναι της μορφής (k, 2k−1), k ∈ ℝ. Γενικά, από την επίλυση ενός γραμμικού συστήματος 2 x 2 αναμένουμε μια μόνο από τις περιπτώσεις : | |||||
Λύση – διερεύνηση γραμμικού συστήματος 2 x 2 Στην παράγραφο αυτή θα παρουσιάσουμε την επίλυση ενός γραμμικού συστήματος 2 x 2 στη γενική του μορφή. Έστω λοιπόν το γραμμικό σύστημα $$\begin{cases} αx + βy = γ \\ α'x + β'y = γ ' \end{cases}$$ Αρχικά θα εξετάσουμε την περίπτωση που είναι β≠0 και β ' ≠0 . Τότε το σύστημα γράφεται : $$\begin{cases} y = - \dfrac{α}{β}x + \dfrac{γ}{β} \quad \quad (\epsilon_{1}) \\ y = - \dfrac{α '}{ β '}x + \dfrac{γ '}{β '} \quad \quad (\epsilon_{2}) \end{cases}$$ και οι εξισώσεις του παριστάνουν ευθείες ε1 και ε2 με αντίστοιχους συντελεστές διεύθυνσης λ1 = - $ \dfrac{α}{β}$ και λ2 = - $ \dfrac{α '}{β '}$ . • Αν - $\dfrac{α}{β} $ ≠ - $\dfrac{α '}{β '}$, δηλαδή αν αβ ' − α' β ≠ 0, τότε οι ευθείες ε1 και ε2 έχουν διαφορετικούς συντελεστές διεύθυνσης, οπότε τέμνονται σε ένα σημείο του οποίου η τετμημένη προσδιορίζεται από την λύση της εξίσωσης - $\dfrac{α\ '}{β\ '}x $ + $\dfrac{γ\ '}{β\ '}$ = - $\dfrac{α}{β}x $ + $\dfrac{γ}{β}$ ⇔ ($\dfrac{α}{β}$ - $\dfrac{α\ '}{β\ '}$)x = $\dfrac{γ}{β}$ - $\dfrac{γ\ '}{β\ '}$ Η τεταγμένη του σημείου τομής είναι : y = - $\dfrac{α}{β}$ ⋅ $(\dfrac{γβ ' - γ 'β}{αβ ' - α 'β})$ + $\dfrac{γ}{β}$ = $\dfrac{-αγβ ' + αβγ ' + γαβ ' - γα 'β}{β (αβ ' - α 'β)}$ = $\dfrac{β(αγ ' - α 'γ)}{β(αβ ' - α 'β)}$ | |||||
Επομένως y = $\dfrac{(αγ ' - α 'γ)}{(αβ ' - α 'β)}$ Άρα, στην περίπτωση αυτή, το σύστημα έχει μοναδική λύση την (x, y) =( $\dfrac{γβ ' - γ 'β}{αβ ' - α 'β}$ , $\dfrac{αγ ' - α 'γ}{αβ ' - α 'β}$) • Αν -$\dfrac{α}{β}$ = -$\dfrac{α '}{β '}$ , δηλαδή αν αβ΄- α΄β = 0 , τότε οι ευθείες ε1 και ε2 έχουν τον ίδιο συντελεστή διεύθυνσης, οπότε ή είναι παράλληλες ή ταυτίζονται. Αυτό σημαίνει ότι το σύστημα ή είναι αδύνατο ή έχει άπειρες λύσεις αντιστοίχως. Στα ίδια συμπεράσματα καταλήγουμε και στην περίπτωση που είναι β=0 ή β' =0. Συνοψίζοντας τα παραπάνω συμπεράσματα για το γραμμικό σύστημα $$\begin{cases} αx + βy = γ \\ α'x + β'y = γ ' \end{cases}$$ Έχουμε : • Αν αβ' − α'β ≠0 το σύστημα έχει μοναδική λύση την (x, y) =( $\dfrac{γβ ' - γ 'β}{αβ ' - α 'β}$ , $\dfrac{αγ ' - α 'γ}{αβ ' - α 'β}$) • Αν αβ' − α'β = 0 το σύστημα έχει άπειρες λύσεις ή είναι αδύνατο. D = $\begin{vmatrix} α & β \\ α ' & β ' \\ \end{vmatrix} $ και λέγεται ορίζουσα του συστήματος Δηλαδή : D = $\begin{vmatrix} α & β \\ α ' & β ' \\ \end{vmatrix} $ = αβ ' - α 'β . Την ορίζουσα που προκύπτει από την D, αν στη θέση των συντελεστών του x θέσουμε τους σταθερούς όρους, συμβολίζουμε με : Dx = $\begin{vmatrix} γ & β \\ γ ' & β ' \\ \end{vmatrix} $ = γβ ' - γ 'β . Ομοίως, την ορίζουσα που προκύπτει από την D, αν στη θέση των συντελεστών του y θέσουμε τους σταθερούς όρους, συμβολίζουμε με : Dy = $\begin{vmatrix} α & γ \\ α ' & γ ' \\ \end{vmatrix} $ = αγ ' - α 'γ . | |||||
Τα προηγούμενα συμπεράσματα τα οποία αφορούν στην επίλυση ενός γραμμικού συστήματος συνοψίζονται, με τη βοήθεια των οριζουσών, ως εξής :
Για παράδειγμα : ✔ Το σύστημα $\begin{cases} x - 2y = 6 \\ 3x + 4y = 8 \end{cases}$ έχει D = $\begin{vmatrix} 1 & -2 \\ 3 & 4 \\ \end{vmatrix} $ = 1 ⋅ 4 - 3(-2) = 4 + 6 = 10 ≠ 0 , οπότε έχει μοναδική λύση. Επειδή Dx = $\begin{vmatrix} 6 & -2 \\ 8 & 4 \\ \end{vmatrix} $ = 24 + 16 = 40 και Dy = $\begin{vmatrix} 1 & 6 \\ 3 & 8 \\ \end{vmatrix} $ = 8 - 18 = -10 έχουμε : x = $\dfrac{D_{x}}{D}$ = $\dfrac{40}{10}$ = 4 και y = $\dfrac{D_{y}}{D}$ = $\dfrac{-10}{10}$ = -1 . Άρα, η μοναδική λύση του συστήματος είναι το ζεύγος (x, y) = (4, −1) . ✔ Το σύστημα $\begin{cases} 2x - 3y = 40 \\ 4x - 6y = 80 \end{cases}$ έχει D = $\begin{vmatrix} 2 & -3 \\ 4 & -6 \\ \end{vmatrix} $ = 2(-6) - 4(-3) = - 12 + 12 = 0 και επομένως το σύστημα αναμένεται ή να είναι αδύνατο ή να έχει άπειρο πλήθος λύσεων. Αν διαιρέσουμε και τα δύο μέλη της δεύτερης εξίσωσης με το 2, τότε το σύστημα γράφεται $\begin{cases} 2x - 3y = 40 \\ 2x - 3y = 40' \end{cases}$ δηλαδή έχει μόνο μία εξίσωση την 2x − 3y = 40. Αυτό σημαίνει ότι οι λύσεις του συστήματος είναι οι λύσεις της εξίσωσης 2x − 3y = 40 ⇔ y = $\dfrac{2x - 40}{3}$ . | |||||
Άρα το σύστημα έχει άπειρο πλήθος λύσεων τα ζεύγη της μορφής (k , $\dfrac{2k - 40}{3}$), k ∈ ℝ ✔ Το σύστημα $\begin{cases} 3x + y = 11 \\ 9x + 3y = 6 \end{cases}$ έχει D = $\begin{vmatrix} 3 & 1 \\ 9 & 3 \\ \end{vmatrix} $ = 9 - 9 = 0 και επομένως το σύστημα αναμένεται ή να είναι αδύνατο ή να έχει άπειρο πλήθος λύσεων. Το σύστημα αυτό γράφεται $\begin{cases} 3x + y = 11 \\ 3x + y = 2 \end{cases}$ που είναι προφανώς αδύνατο. ΕΦΑΡΜΟΓΗ 1η Να λυθεί το σύστημα $\begin{cases} λx - y = λ - 1 \\ λ^2 x - 2y = λ \end{cases}$ ΛΥΣΗ Παρατηρούμε ότι οι συντελεστές και οι σταθεροί όροι του συστήματος δεν είναι όλοι συγκεκριμένοι αριθμοί, αλλά εξαρτώνται από το λ. Πρέπει επομένως για τις διάφορες τιμές του λ, να εξετάσουμε πότε προκύπτει σύστημα που έχει μοναδική λύση την οποία και να βρούμε ή πότε προκύπτει σύστημα αδύνατο ή σύστημα με άπειρες λύσεις. Όπως και στις εξισώσεις, ο λ λέγεται παράμετρος και η εργασία αυτή λέγεται διερεύνηση. • Υπολογίζουμε τις ορίζουσες D, Dx, Dy . Έχουμε : D = $\begin{vmatrix} λ & -1 \\ λ^2 & -2 \\ \end{vmatrix} $ =$ -2λ + λ^2 = λ (λ - 2)$ | |||||
• Βρίσκουμε τις τιμές της παραμέτρου, για τις οποίες είναι D = 0 . Έχουμε : D = 0 ⇔ λ(λ - 2) = 0 ⇔ λ = 0 ή λ = 2 Διακρίνουμε τις περιπτώσεις : ✔ Αν D ≠0 , δηλαδή αν και λ ≠0 και λ ≠ 2, τότε το σύστημα έχει μοναδική λύση (x, y), με : x = $\dfrac{D_{x}}{D}$ = $\dfrac{2 - λ}{λ (λ - 2)}$ = $ \dfrac{- (λ - 2_)}{λ(λ - 2)}$ = - $\dfrac{1}{λ}$ και
✔ Αν D = 0 ,δηλαδή αν λ = 0 ή λ = 2 , τότε το σύστημα ή είναι αδύνατο ή έχει άπειρες λύσεις. • Αν λ = 0 , τότε το σύστημα γράφεται $\begin{cases} 0x - y = -1 \\ 0x - 2y = 0 \end{cases}$ ⇔ $\begin{cases} y = 1 \\ y = 0 \end{cases}$ και άρα είναι αδύνατο. $\begin{cases} 2x - y = 1 \\ 4x - 2y = 2 \end{cases}$ ⇔ $\begin{cases} 2x - y = 1 \\ 2x - y = 1 \end{cases}$ και άρα έχει άπειρο πλήθος λύσεων. Επειδή , 2x - y = 1 ⇔ y = 2x - 1 , Οι λύσεις του συστήματος είναι όλα τα ζεύγη της μορφής (k, 2k - 1), k ∈ ℝ
Γραμμικό Σύστημα 3 x 3 | |||||
Όταν έχουμε τρεις γραμμικές εξισώσεις με τρεις αγνώστους : α1x + β1y + γ1z=δ1 , α2x + β2y + γ2z=δ2 και α3x + β3y + γ3z=δ3 και ζητάμε τις κοινές λύσεις τους, τότε λέμε ότι έχουμε να λύσουμε ένα γραμμικό σύστημα τριών εξισώσεων με τρεις αγνώστους ή, πιο σύντομα, ένα γραμμικό σύστημα 3 x 3 και γράφουμε $\begin{cases} α_{1}x + β_{1}y + γ_{1}z = δ_{1} \\ α_{2}x + β_{2}y + γ_{2}z = δ_{2} \\ α_{3}x + β_{3}y + γ_{3}z = δ_{3}\end{cases}$ Για την επίλυση ενός τέτοιου συστήματος χρησιμοποιούμε μεθόδους ανάλογες με τις μεθόδους που χρησιμοποιήσαμε για την επίλυση ενός γραμμικού συστήματος 2 x 2 . Έστω για παράδειγμα ότι θέλουμε να λύσουμε το σύστημα $\begin{cases} 2x - y + 3z = -9 \quad ({1})\\ x + 3y - z = 10 \quad \quad ({2})\\ 3x + y - z = 8 \quad \quad ({3})\end{cases}$ Θα χρησιμοποιήσουμε τη μέθοδο της αντικατάστασης. Λύνουμε τη μία από τις τρεις εξισώσεις ως προς έναν άγνωστο, π.χ. την (3) ως προς z, και αντικαθιστούμε στις άλλες δύο. Έτσι έχουμε : 3x + y - z = 8 ⇔ z = 3x + y - 8 (4)
✔ 2x - y + 3z = -9 ⇔ 2x - y + 3(3x + y - 8) = -9 ⇔ 11x + 2y = 15 (5)
$\begin{cases} 11x + 2y = 15 \\ -x + y = 1 \end{cases}$ , από την επίλυση του οποίου βρίσκουμε ότι x=1 και y=2 . ΣΧΟΛΙΟ Επειδή η επίλυση ενός γραμμικού συστήματος 3 x 3, όπως είδαμε παραπάνω, ανάγεται στην επίλυση ενός γραμμικού συστήματος 2 x 2, προκύπτει ότι και ένα γραμμικό σύστημα 3 x 3 ή έχει μοναδική λύση ή είναι αδύνατο ή έχει άπειρο πλήθος λύσεων. | |||||
ΑΣΚΗΣΕΙΣ
|
| ||||||||||||||
| ||||||||||||||