4.1 ΑΝΙΣΩΣΕΙΣ 1ου ΒΑΘΜΟΥ

Οι ανισώσεις: αx + β > 0 και αx + β < 0

Γνωρίσαμε στο Γυμνάσιο τη διαδικασία επίλυσης μιας ανίσωσης της μορφής αx + β > 0 ή της μορφής αx + β < 0 , με α και β συγκεκριμένους αριθμούς.

Γενικότερα έχουμε:

αx + β > 0 ⇔ αx + β - β > -β
⇔αx > -β

Διακρίνουμε τώρα τις εξής περιπτώσεις:

• Αν α > 0, τότε:

• Αν α < 0, τότε:

• Αν α = 0, τότε η ανίσωση γίνεται 0x > -β, η οποία

• αληθεύει για κάθε x $\in$ ℝ, αν είναι β > 0, ενώ

• είναι αδύνατη, αν είναι β $\le$ 0 .

Για παράδειγμα:

• Η ανίσωση 4x > 8 γράφεται:

$4x \gt 8$ ⇔ $x \gt \dfrac{8}{4}$ ⇔ $x \gt 2.$

Επομένως η ανίσωση αυτή αληθεύει για x $\in$ (2, +∞)

• Η ανίσωση -4x > 8 γράφεται:

$-4x \gt 8$ ⇔ $x \lt -\dfrac{8}{4}$ ⇔ $x \lt -2.$

Επομένως η ανίσωση αυτή αληθεύει για x $\in$(-∞,-2).

• Η ανίσωση 0x > -2 αληθεύει για κάθε x $\in$ ℝ , ενώ η ανίσωση 0x > 2 είναι αδύνατη.

ΕΦΑΡΜΟΓΗ

i) Να λυθούν οι ανισώσεις:

$2(x+4)-(x+6) \lt 12-x$      και      $2x + \dfrac{x}{6} +\dfrac{5}{3} \geq 2(1+x)$

ii) Να βρεθούν οι κοινές λύσεις των δύο ανισώσεων.

ΛΥΣΗ

i) Για την πρώτη ανίσωση έχουμε:

Άρα η ανίσωση αληθεύει για κάθε πραγματικό αριθμό x < 5 .

Για τη δεύτερη ανίσωση έχουμε:

Άρα η ανίσωση αληθεύει για κάθε πραγματικό αριθμό x ≥ 2

ii) Επειδή η πρώτη ανίσωση αληθεύει για x < 5 και η δεύτερη για x ≥ 2, οι ανισώσεις συναληθεύουν για κάθε πραγματικό αριθμό x με 2 ≤ x < 5 , δηλαδή οι ανισώσεις συναληθεύουν όταν x $\in$ [2,5).

Για τον προσδιορισμό των κοινών λύσεων των δύο ανισώσεων μας διευκολύνει να παραστήσουμε τις λύσεις τους στον ίδιο άξονα (Σχήμα), απ’ όπου προκύπτει ότι 2 ≤ x < 5

Ανισώσεις με απόλυτες τιμές

Με τη βοήθεια των ιδιοτήτων της απόλυτης τιμής και της έννοιας της απόστασης δύο αριθμών, μπορούμε να επιλύουμε ανισώσεις που περιέχουν απόλυτες τιμές. Στη συνέχεια θα δούμε μερικά παραδείγματα επίλυσης τέτοιων ανισώσεων.

ΠΑΡΑΔΕΙΓΜΑ 1o

Να λυθεί η ανίσωση: |x - 2| < 3 .

ΛΥΣΗ

Η επίλυση της ανίσωσης |x - 2| < 3,με τη βοήθεια της ιδιότητας

|x - x_ο| < ρ ⇔ x_ο - ρ < x < x_ο + ρ

γίνεται ως εξής:

|x - 2| < 3 ⇔ 2 - 3 < x < 2 + 3
⇔ -1 < x < 5

Μπορούμε όμως να λύσουμε την παραπάνω ανίσωση και με τη βοήθεια της ιδιότητας

|x| < ρ ⇔ -ρ < x < ρ

ως εξής:

Άρα η ανίσωση αληθεύει για x $\in$(-1,5).

ΠΑΡΑΔΕΙΓΜΑ 2o

Να λυθεί η ανίσωση: |2x -1| > 5

ΛΥΣΗ

Από την ιδιότητα |x| > ρ ⇔ x < -ρ ή x > ρ έχουμε :

Άρα η ανίσωση αληθεύει για x $\in$(-∞,-2) U (3,+∞).

4.2 ΑΝΙΣΩΣΕΙΣ 2^ου ΒΑΘΜΟΥ

Μορφές τριωνύμου

Η παράσταση αx² + βx + γ, α ≠ 0 λέγεται τριώνυμο 2^ου βαθμού ή, πιο απλά, τριώνυμο. Η διακρίνουσα Δ της αντίστοιχης εξίσωσης αx² + βx + γ = 0 λέγεται και διακρίνουσα του τριωνύμου. Οι ρίζες της εξίσωσης αx² + βx + γ = 0, δηλαδή οι $x_1 = \dfrac{-β + \sqrt{Δ}}{2α}$ και $x_2 = \dfrac{-β - \sqrt{Δ}}{2α}$ ονομάζονται και ρίζες του τριωνύμου.

Το τριώνυμο αx² + βx + γ, α ≠ 0 μετασχηματίζεται ως εξής:

Επομένως:

$αx^2 + βx + γ = α \left[\left(x+\dfrac{β}{2α}\right)^2 - \dfrac{Δ}{4α^2}\right]$      (1)

Διακρίνουμε τώρα τις εξής περιπτώσεις:

• Δ > 0 . Τότε ισχύει $Δ = (\sqrt{Δ})^2$, οπότε έχουμε:

Επομένως:

αx² + βx + γ = α(x - x₁)(x - x₂) ,

όπου x₁, x₂ οι ρίζες του τριωνύμου.

Άρα, όταν Δ > 0, τότε το τριώνυμο μετατρέπεται σε γινόμενο του α επί δύο πρωτοβάθμιους παράγοντες.

• Δ = 0 . Τότε από την ισότητα (1) έχουμε:

$αx^2 + βx + γ = α \left(x+\dfrac{β}{2α}\right)^2$.

Άρα, όταν Δ = 0, τότε το τριώνυμο μετατρέπεται σε γινόμενο του α επί ένα τέλειο τετράγωνο.

• Δ < 0 . Τότε ισχύει |Δ| = -Δ, οπότε έχουμε:

$αx^2 + βx + γ = α \left[\left(x+\dfrac{β}{2α}\right)^2+\dfrac{\lvert Δ \rvert}{4α^2}\right]$.

Επειδή για κάθε x $\in$ ℝ , η παράσταση μέσα στην αγκύλη είναι θετική, το τριώνυμο δεν αναλύεται σε γινόμενο πρωτοβάθμιων παραγόντων.

Συνοψίζοντας τα παραπάνω συμπεράσματα για τις μορφές του τριωνύμου αx² + βx + γ, α ≠ 0 με διακρίνουσα Δ έχουμε:

Για παράδειγμα:

• Το τριώνυμο 2x² + 3x - 2 έχει Δ = 9 + 16 = 25 > 0 και ρίζες $x_1 = \dfrac{1}{2}$ και $x_2=-2.$. Επομένως:

$2x^2+3x-2 = 2\left(x-\dfrac{1}{2}\right)(x+2) = (2x-1)(x+2).$

• Το τριώνυμο $\dfrac{1}{2}x^2+3x+\dfrac{9}{2}$ έχει $Δ=9-4\cdot \dfrac{1}{2} \cdot \dfrac{9}{2} = 0$ και $\dfrac{β}{2α} = -3.$ Eπομένως:

$\dfrac{1}{2}x^2 + 3x + \dfrac{9}{2} = \dfrac{1}{2}(x-3)^2$.

• Το τριώνυμο 2x² - 6x + 5 έχει Δ= - 4 < 0 . Επομένως:

$2x^2 - 6x +5=2\left[\left(x-\dfrac{3}{2}\right)^2 + \dfrac{1}{4}\right]$.

Πρόσημο των τιμών του τριωνύμου

Για να μελετήσουμε το πρόσημο των τιμών του τριωνύμου αx² + βx + γ, α ≠ 0, θα χρησιμοποιήσουμε τις μορφές του ανάλογα με τη διακρίνουσα.

• Αν Δ > 0, τότε, όπως είδαμε προηγουμένως, ισχύει:

αx² + βx + γ= α (x - x₁ )(x - x₂) (1)

Υποθέτουμε ότι x₁ < x₂ και τοποθετούμε τις ρίζες σε έναν άξονα.

Παρατηρούμε ότι:

Αν x < x1 < x2 (Σχήμα) , τότε x - x1 < 0 και x - x2 < 0, οπότε (x - x1)(x - x2) > 0. Επομένως, λόγω της (1), το τριώνυμο είναι ομόσημο του α .
Αν x1 < x < x2 (Σχήμα), τότε x - x1 > 0 και x - x2 < 0, οπότε (x - x1)(x - x2) < 0. Επομένως, λόγω της (1), το τριώνυμο είναι ετερόσημο του α .
Αν x1 < x2 < x (Σχήμα), τότε x - x1 > 0 και x - x2 > 0, οπότε (x - x1)(x - x2) > 0. Επομένως, λόγω της (1), το τριώνυμο είναι ομόσημο του α .

• Αν Δ = 0, τότε ισχύει:

$αx^2 + βx +γ = α \left(x + \dfrac{β}{2α}\right)^2$.

Επομένως, το τριώνυμο είναι ομόσημο του α για κάθε πραγματικό x ≠ $-\dfrac{β}{2α}$ , ενώ μηδενίζεται για x = $-\dfrac{β}{2α}$.

• Αν Δ < 0, τότε ισχύει:

$αx^2 + βx + γ = α \left[\left(x+\dfrac{β}{2α}\right)^2+\dfrac{\lvert Δ \rvert}{4α^2}\right]$.

Όμως η παράσταση μέσα στην αγκύλη είναι θετική για κάθε πραγματικό αριθμό x. Επομένως το τριώνυμο είναι ομόσημο του α σε όλο το ℝ.

Τα παραπάνω συνοψίζονται στον πίνακα:

Μικροπείραμα

Ανισώσεις της μορφής αx² + βx + γ > 0 ή αx² + βx + γ < 0

Τα προηγούμενα συμπεράσματα χρησιμοποιούνται στην επίλυση ανισώσεων της μορφής αx² + βx + γ > 0 ή αx² + βx + γ < 0, α ≠ 0 , τις οποίες ονομάζουμε ανισώσεις δευτέρου βαθμού. Ο τρόπος επίλυσης αυτών φαίνεται στα παρακάτω παραδείγματα.

Μικροπείραμα

ΠΑΡΑΔΕΙΓΜΑ 1o

Να λυθούν οι ανισώσεις

i) 2x² - 3x - 2 > 0 ii) 2x² - 3x - 2 < 0

ΛΥΣΗ

Ζητάμε τις τιμές του x, για τις οποίες το τριώνυμο 2x² - 3x - 2 είναι θετικό στην περίπτωση (i) και αρνητικό στην περίπτωση (ii).

Το τριώνυμο έχει ρίζες τους αριθμούς $-\dfrac{1}{2}$ και 2 και, επειδή α = 2 > 0, το πρόσημό του φαίνεται στον παρακάτω πίνακα.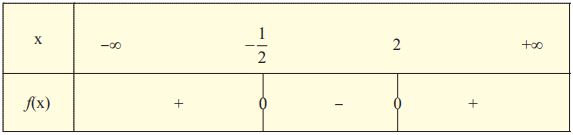

Από τον πίνακα αυτόν προκύπτει ότι:

i)     Η ανίσωση 2x² - 3x - 2 > 0 έχει λύσεις τα x $\in$ ℝ για τα οποία ισχύει $x \lt -\dfrac{1}{2}$ ή x > 2 , δηλαδή τα $x \in \left(-\infty, -\dfrac{1}{2}\right) \cup (2,+\infty)$. Οι λύσεις αυτές εποπτικά φαίνονται στο παρακάτω σχήμα.

ii) Η ανίσωση 2x² - 3x - 2 < 0 έχει λύσεις τα x $\in$ℝ για τα οποία ισχύει $-\dfrac{1}{2} \lt x \lt 2$, δηλαδή τα $x \in \left(-\dfrac{1}{2},2\right) $. Οι λύσεις αυτές εποπτικά φαίνονται στο παρακάτω σχήμα.

ΠΑΡΑΔΕΙΓΜΑ 2o

Να λυθεί η ανίσωση 2x² - 3x - 2 ≤ 0

ΛΥΣΗ

Ζητάμε τις τιμές του x, που είναι λύσεις της ανίσωσης 2x² - 3x - 2 < 0 ή ρίζες της εξίσωσης 2x² - 3x - 2 = 0. Επομένως σύμφωνα με το 1^o παράδειγμα οι λύσεις της ανίσωσης 2x² - 3x - 2 ≤ 0 είναι τα x$\in$ℝ , με $-\dfrac{1}{2} \le x \le 2$, δηλαδή τα $x \in \left[-\dfrac{1}{2},2\right]$. Οι λύσεις αυτές εποπτικά φαίνονται στο παρακάτω σχήμα.

Μικροπείραμα

ΠΑΡΑΔΕΙΓΜΑ 3o

Να λυθούν οι ανισώσεις

i) x² - 2x + 1 > 0 ii) x² - 2x + 1 < 0

ΛΥΣΗ

Η διακρίνουσα του τριωνύμου x² - 2x + 1 είναι Δ = 0, οπότε έχει διπλή ρίζα την x = 1. Άρα το τριώνυμο είναι ομόσημο του α = 1, δηλαδή θετικό, για κάθε x$\in$ℝ με x ≠ 1.

Επομένως οι λύσεις της ανίσωσης (i) είναι όλοι οι πραγματικοί αριθμοί x, με x ≠ 1, ενώ η ανίσωση (ii) είναι αδύνατη.

Οι λύσεις της (i) εποπτικά φαίνονται στο παρακάτω σχήμα.

ΠΑΡΑΔΕΙΓΜΑ 4o

Να λυθεί η ανίσωση x² + x + 1 > 0.

ΛΥΣΗ

Η διακρίνουσα του τριωνύμου x² + x + 1 είναι Δ = -3 < 0, οπότε το τριώνυμο είναι ομόσημο του α = 1, δηλαδή θετικό, για κάθε x$\in$ℝ . Επομένως οι λύσεις της ανίσωσης είναι όλοι οι πραγματικοί αριθμοί.

ΕΦΑΡΜΟΓΕΣ

1. Να βρεθούν οι τιμές του x$\in$ℝ για τις οποίες συναληθεύουν οι ανισώσεις:

x² - 4x - 5 < 0 και x² - x - 6 > 0.

ΛΥΣΗ

Λύνουμε κάθε ανίσωση χωριστά και μετά βρίσκουμε τις κοινές λύσεις

Έχουμε:

• x² - 4x - 5 < 0 ⇔ (x - 5)(x +1) < 0 ⇔ -1< x < 5

• x² - x - 6 > 0 ⇔ (x + 2)(x - 3) > 0 ⇔ x < -2 ή x > 3

Άρα οι ανισώσεις συναληθεύουν για x$\in$(3,5).

2. Δίνεται η εξίσωση x² - (α + 1)x + α + 4 = 0, α$\in$ℝ

i) Να βρεθεί η διακρίνουσα της εξίσωσης και να μελετηθεί το πρόσημό της.

ii) Για ποιες τιμές του α η εξίσωση έχει δύο ρίζες άνισες;

iii) Για ποιες τιμές του α η εξίσωση έχει διπλή ρίζα;

iv) Για ποιες τιμές του α η εξίσωση είναι αδύνατη στο ℝ ;

ΛΥΣΗ

i) Έχουμε:

Δ = [-(α +1)]² - 4 · 1 · (α + 4) = α² - 2α - 15.

Παρατηρούμε ότι η διακρίνουσα είναι ένα τριώνυμο του α με διακρίνουσα

Δ' = (-2 )² - 4 · 1 · (-15) = 64 > 0.

Επομένως η διακρίνουσα Δ έχει ρίζες:

$α_1 = \dfrac{2+8}{2} = 5$     και     $α_2 = \dfrac{2-8}{2} = -3$.

και το πρόσημό της φαίνεται στον παρακάτω πίνακα.

Από τον πίνακα αυτό προκύπτει ότι:

ii) Η εξίσωση έχει δύο ρίζες άνισες αν Δ > 0 , δηλαδή αν α < -3 ή α > 5.

iii) Η εξίσωση έχει μία διπλή ρίζα αν Δ = 0 , δηλαδή αν α = -3 ή α = 5.

iv) Η εξίσωση είναι αδύνατη αν Δ < 0, δηλαδή -3 < α < 5.

4.3 ΑΝΙΣΩΣΕΙΣ ΓΙΝΟΜΕΝΟ & ΑΝΙΣΩΣΕΙΣ ΠΗΛΙΚΟ

Πρόσημο γινομένου

Έστω ότι θέλουμε να μελετήσουμε ένα γινόμενο P(x) = Α(x) · Β(x) · … · Φ(x) ως προς το πρόσημό του, όπου οι παράγοντες Α(x), Β(x) , … , Φ(x) είναι της μορφής αx + β (πρωτοβάθμιοι) ή της μορφής αx² + βx + γ (τριώνυμα).

Βρίσκουμε το πρόσημο κάθε παράγοντα χωριστά και στη συνέχεια το πρόσημο του P(x), όπως φαίνεται στο παράδειγμα που ακολουθεί.

ΠΑΡΑΔΕΙΓΜΑ

Να βρεθεί για τις διάφορες τιμές του x$\in$ℝ το πρόσημο του γινομένου

P(x) = (x - 1) (x² + x - 6)(2x² + x + 1) .

ΛΥΣΗ

Αρχικά βρίσκουμε το πρόσημο του κάθε παράγοντα χωριστά ως εξής:

• Επειδή

x - 1 ≥ 0 ⇔ x ≥ 1,

το x - 1 είναι θετικό για x > 1, μηδέν για x = 1 και αρνητικό για x < 1.

• Επειδή

x² + x - 6 ≥ 0 ⇔ (x + 3)(x - 2) ≥ 0 ⇔ x ≤ -3 ή x ≥ 2,

το x² + x - 6 είναι θετικό για x < -3 και για x > 2 , μηδέν για x = -3 και για x = 2 και αρνητικό για -3 < x < 2 .

• Επειδή το 2x² + x +1 έχει διακρίνουσα Δ = 1 - 8 = -7 < 0, το τριώνυμο αυτό είναι θετικό για κάθε x$\in$ℝ .

Ο προσδιορισμός, τώρα, του προσήμου του γινομένου P(x) γίνεται με τη βοήθεια του παρακάτω πίνακα, εφαρμόζοντας τον κανόνα των προσήμων.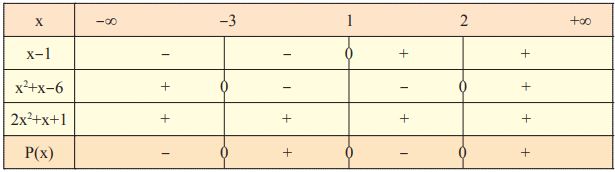

Ώστε το γινόμενο P(x) είναι θετικό για -3 < x < 1 και για x > 2, ενώ είναι αρνητικό για x < -3 και για 1 < x < 2. Τέλος είναι μηδέν για x = -3, για x = 1 και για x = 2 .

Ανισώσεις της μορφής Α(x) · Β(x) · … · Φ(x) > 0 (< 0)

Άμεση εφαρμογή των παραπάνω έχουμε στην επίλυση ανισώσεων της μορφής Α(x) · Β(x) · … · Φ(x) > 0 (< 0), όπως είναι για παράδειγμα η ανίσωση

(x - 1)(x² + x - 6)(2x² + x + 1) < 0

Προκειμένου να λύσουμε την ανίσωση αυτή αρκεί να βρούμε τις τιμές του x$\in$ℝ για τις οποίες το γινόμενο P(x) = (x - 1)(x² + x - 6)(2x² + x + 1)είναι αρνητικό.

Από την πρώτη και την τελευταία γραμμή του πίνακα προσήμου του P(x) διαπιστώνουμε ότι η ανίσωση αληθεύει όταν x$\in$(-∞, -3) ⋃ (1,2) .

Ανισώσεις της μορφής

Όπως γνωρίζουμε το πηλίκο και το γινόμενο δύο αριθμών είναι ομόσημα.

Επομένως:

$\dfrac{A(x)}{B(x)} \gt 0$ ⇔ $A(x) \cdot B(x) \gt 0$      και      $\dfrac{A(x)}{B(x)} \lt 0$ ⇔ $A(x) \cdot B(x) \lt 0$,

αφού, καμία από τις λύσεις της Α(x) · Β(x) > 0 και της Α(x) · Β(x) < 0 δεν μηδενίζει το Β(x).

Για παράδειγμα , έστω ότι θέλουμε να λύσουμε την ανίσωση

$\dfrac{(x-1)(2x^2+x+1)}{x^2+x-6} \gt 0.$

Η ανίσωση αυτή είναι ισοδύναμη με την

(x - 1)(x² + x - 6)(2x² + x + 1) > 0,

δηλαδή με την P(x) > 0 , η οποία, από τον πίνακα προσήμου του P(x) αληθεύει όταν x$\in$(-3,1) ⋃ (2, +∞) .

ΣΧΟΛΙΟ

Μία ανίσωση της μορφής $\dfrac{A(x)}{B(x)} \geq 0$ αληθεύει για εκείνους τους πραγματικούς αριθμούς x για τους οποίους ισχύουν συγχρόνως

Α(x) · Β(x) > 0 και Β(x) ≠ 0.

Έστω για παράδειγμα η ανίσωση $\dfrac{x^2-4x+3}{x^2+3x-4} \geq 0$. Έχουμε:

$\dfrac{x^2-4x+3}{x^2+3x-4} \geq 0$ ⇔ $(x^2-4x+3)(x^2+3x-4) \geq 0$ και $x^2+3x-4$ ≠ 0

Οι ρίζες του τριωνύμου x² - 4x + 3 είναι οι 1 και 3, ενώ του τριωνύμου x² + 3x - 4 είναι οι 1 και -4.

Συντάσσουμε τον πίνακα προσήμου του γινομένου:

P(x) = (x² - 4x + 3)(x² + 3x - 4)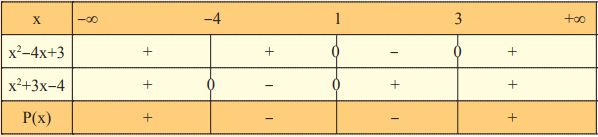

Άρα η ανίσωση αληθεύει όταν x $\in$(-∞, -4) ⋃ [3, +∞) .