Μαθηματικά (Ε' Δημοτικού) - Βιβλίο Μαθητή (Εμπλουτισμένο)
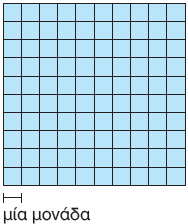
Σχεδιάζουμε στο διπλανό τετραγωνισμένο χαρτί ένα τετράγωνο με μήκος πλευράς 5 μονάδες και μετά υπολογίζουμε το εμβαδό του.
Σχεδιάζουμε στο διπλανό τετραγωνισμένο χαρτί ένα ορθογώνιο με μήκος 5 μονάδες και πλάτος 3 μονάδες και μετά υπολογίζουμε το εμβαδό του.
Σχεδιάζουμε τη μία διαγώνιό του ενώνοντας δύο μη διαδοχικές κο-ρυφές του.
Σχεδιάζουμε στο διπλανό τετραγωνισμένο χαρτί ένα ορθογώνιο τρίγωνο και υπολογίζουμε το εμβαδό του.
| Βασικές μαθηματικές έννοιες και διεργασίες |
|
Παραδείγματα |
| Για να υπολογίσουμε το εμβαδό ενός τετραγώνου, πολλαπλασιάζουμε το μήκος της πλευράς του επί τον εαυτό της. |
|
Ετετραγ. = μήκος πλευράς $\text{☓}$ μήκος πλευράς = 2 μονάδες $\text{☓}$ 2 μονάδες = 4 τετ. μονάδες |
| Για να υπολογίσουμε το εμβαδό ενός ορθογωνίου, πολλαπλασιάζουμε το μήκος επί το πλάτος του, όταν αυτά μετριούνται με την ίδια μονάδα μέτρησης. |
|
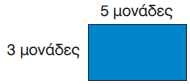
Εορθογ. = μήκος $\text{☓}$ πλάτος = 5 μονάδες $\text{☓}$ 3 μονάδες = 15 τετ. μονάδες |
| Για να υπολογίσουμε το εμβαδό ενός ορθογώνιου τριγώνου, πολλαπλασιάζουμε τα μήκη των κάθετων πλευρών του, όταν αυτά μετριούνται με την ίδια μονάδα μέτρησης, και μετά διαιρούμε το γινόμενο αυτό με το 2. |
|
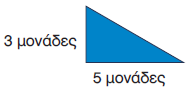
Εορθ.τριγώνου = $\dfrac{\sf{μήκος κάθ.πλευράς \text{☓} μήκος κάθ.πλευράς}}{2}$ = = $\dfrac{3 \text{☓} 5}{2}$ = $\dfrac{15}{2}$ = 7,5 τετ. μονάδες |
Ένας κήπος σε σχήμα τετραγώνου έχει εμβαδό 36 τ.μ. Να βρείτε την περίμετρό του.
Το εμβαδό ενός τετραγώνου είναι ίσο με το γινόμενο του μήκους της πλευράς του επί τον εαυτό της. Ο αριθμός που, όταν πολλαπλασιαστεί με τον εαυτό του, δίνει γινόμενο 36, είναι ο 6. Επομένως το τετράγωνο με εμβαδό 36 τ.μ. έχει μήκος πλευράς ..............., άρα η περίμετρός του είναι: ..............................................................
