
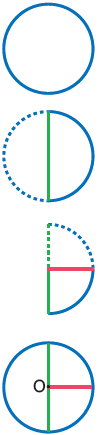
1.Γνωρίζουμε το σχήμα του κύκλου:
1. Κόβουμε προσεχτικά τον μπλε κύκλο από το παράρτημα.
2. Διπλώνουμε το χαρτί σε δύο ίσα μέρη. Ζωγραφίζουμε πράσινη τη γραμμή δίπλωσής του.
3. Διπλώνουμε και πάλι το χαρτί, ώστε να σχηματιστούν τέσσερα ίσα μέρη.
Ζωγραφίζουμε κόκκινη τη δεύτερη γραμμή δίπλωσής του.
4. Ζωγραφίζουμε μαύρο το σημείο Ο στο οποίο τέμνονται οι γραμμές δίπλωσης.
α. Ονομάζουμε την πράσινη και την κόκκινη γραμμή και το σημείο Ο.
πράσινη: …….....……… κόκκινη: …….....… σημείο Ο: …....….………
β. Παρατηρώντας το σχήμα του κύκλου, συμπληρώνουμε τις προτάσεις.
2.Εντοπίζουμε το σχήμα του κύκλου σε αντικείμενα της τάξης μας και:

α. Με μια μεζούρα ή με ένα κομμάτι σπάγκου και χάρακα μετράμε το μήκος κύκλου και τη διάμετρο του κάθε αντικειμένου.
β. Συμπληρώνουμε τον πίνακα και υπολογίζουμε με την αριθμομηχανή.

| Αντικείμενα | μήκος κύκλου (σε εκ.) |
διάμετρος (σε εκ.) |
μήκος κύκλου: διάμετρος (σε εκ.) |
|---|---|---|---|
| χάρτινος κύκλος | |||
| χείλος ποτηριού | 24,7 | 7,8 | 3,17 |
γ. Τοποθετούμε το αποτέλεσμα κάθε διαίρεσης στην αριθμογραμμή:


| Βασικές μαθηματικές έννοιες και διεργασίες |
|
Παραδείγματα |
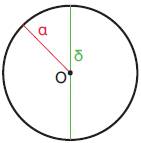
| Τα κύρια στοιχεία του κύκλου είναι: το κέντρο Ο, η ακτίνα α και η διάμετρος δ. |
|
Η διάμετρος του κύκλου είναι 3 εκ. Επομένως: μήκος κύκλου = π x δ=3,14 x 3=9,42 εκ. |
| Για να υπολογίσουμε το μήκος κύκλου, πολλαπλασιάζουμε τον αριθμό π με τη διάμετρο του κύκλου. μήκος κύκλου = π x δ = 3,14 x δ |
|
|
| Ο αριθμός που συμβολίζεται με το ελληνικό γράμμα π είναι με προσέγγιση εκατοστού 3,14. |
|
|
| Ιστορικό σημείωμα Από την αρχαιότητα μέχρι σήμερα, το πηλίκο της διαίρεσης του μήκους οποιουδήποτε κύκλου με τη διάμετρό του προσεγγίζεται όλο και με μεγαλύτερη ακρίβεια και είναι ο αριθμός 3,14159265… που έχει άπειρα δεκαδικά ψηφία. Ο αριθμός αυτός συμβολίζεται σε όλον τον κόσμο με το ελληνικό γράμμα π και στους υπολογισμούς χρησιμοποιούμε την προσεγγιστική του τιμή 3,14. |
||

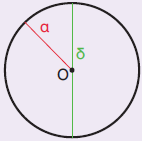
1. Να υπολογίσετε το μήκος ενός κύκλου ακτίνας 3 εκ.
Το μήκος του κύκλου είναι: μήκος κύκλου =3,14 $\text{☓}$ δ
Επειδή η διάμετρος ενός κύκλου είναι διπλάσια της ακτίνας, έχουμε:
μήκος κύκλου = 3,14 $\text{☓}$ 2 $\text{☓}$ ……. = 3,14 $\text{☓}$ ……. =…….. εκ.
2. Να υπολογίσετε την ακτίνα ενός κύκλου που το μήκος του είναι 15,7 εκ.
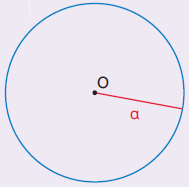
Το μήκος του κύκλου είναι: μήκος κύκλου =3,14 $\text{☓}$ δ
Αφού το μήκος του κύκλου είναι 15,7, έχουμε:
δ = 15,7: 3,14 άρα : δ = ………..
Για να βρούμε την ακτίνα, θα διαιρέσουμε τη διάμετρο διά δύο.
Άρα α= ...... : ......=....... εκ.
