Μαθηματικά (Ε' Δημοτικού) - Βιβλίο Μαθητή (Εμπλουτισμένο)

Συμμετρία

43

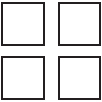
Εικόνα

Διερεύνηση

Εικόνα

1.Συνδυάζουμε μεταξύ τους 4 ίδια τετράγωνα, έτσι ώστε το σχήμα που θα προκύψει να έχει έναν ή περισσότερους άξονες συμμετρίας.

  • Σχεδιάζουμε τα σχήματα που φτιάξαμε στο μιλιμετρέ χαρτί.
  • Σχεδιάζουμε τους άξονες συμμετρίας σε κάθε σχήμα, όπως στο παράδειγμα:


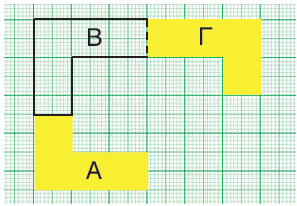
Εικόνα
Εικόνα

Συζητάμε στην τάξη πόσα διαφορετικά σχήματα βρήκαμε.

Εικόνα

2.Ο Νίκος άλλαξε το σχήμα Α στο σχήμα Γ χρησιμοποιώντας διαδοχικά άξονες συμμετρίας.


  • Σκεφτόμαστε δύο διαφορετικούς τρόπους, για να κάνουμε το ίδιο.
Εικόνα








Εικόνα

Συζητάμε στην τάξη τις αλλαγές που αναμένουμε στο αρχικό σχήμα, αν ο άξονας συμμετρίας κόβει το σχήμα ή αν βρίσκεται εκτός του σχήματος.

Συμμετρία

Ενότητα 7

Βασικές μαθηματικές έννοιες και διεργασίες

 

 Παραδείγματα
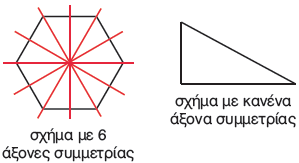
Ένα σχήμα έχει άξονα συμμετρίας μία ευθεία γραμμή, όταν μπορεί να χωριστεί σε δύο τμήματα, ώστε το ένα να συμπίπτει με το άλλο, διπλώνοντας το χαρτί κατά μήκος αυτής της γραμμής.
  • Η ευθεία αυτή ονομάζεται άξονας συμμετρίας του σχήματος.
  • Ένα σχήμα μπορεί να έχει κανένα, ένα, δύο ή περισσότερους άξονες συμμετρίας.

 
Εικόνα
Μπορούμε να βρούμε το συμμετρικό ενός σχήματος ως προς κάποια ευθεία, που την ονομάζουμε άξονα συμμετρίας, όταν διπλώσουμε το χαρτί κατά μήκος της ευθείας αυτής.

 
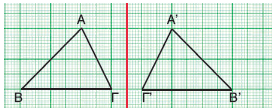
Εικόνα
Εικόνα

Εφαρμογή

Να σχεδιάσετε το συμμετρικό του σχήματος ΑΒΓΔ ως προς άξονα συμμετρίας την κόκκινη ευθεία.

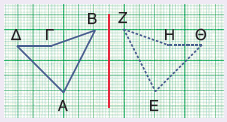
Εικόνα

α. Διπλώνοντας το χαρτί κατά μήκος της κόκκινης ευθείας, βρίσκουμε το συμμετρικό του σχήματος ΑΒΓΔ, που είναι το ΕΖΗΘ.

  • Τα συμμετρικά σημεία των Α, Β, Γ, Δ είναι αντίστοιχα τα σημεία Ε, Ζ, Η, Θ.
  • Όπως γίνεται φανερό με τη δίπλωση, τα συμμετρικά σημεία απέχουν το ίδιο από τον άξονα συμμετρίας.

β. Βρίσκουμε την απόσταση του σημείου Α από τον άξονα συμμετρίας. Το συμμετρικό του σημείο Ε βρίσκεται σε ίση απόσταση από τον άξονα συμμετρίας.

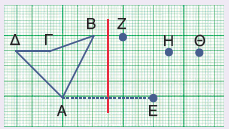
Εικόνα
  • Με τον ίδιο τρόπο βρίσκουμε τα σημεία Ζ, Η, Θ.

γ. Ενώνουμε τα σημεία Ε, Ζ, Η, Θ και σχεδιάζουμε το σχήμα ΕΖΗΘ που είναι συμμετρικό του ΑΒΓΔ ως προς την κόκκινη ευθεία, που είναι ο άξονας συμμετρίας.

Εικόνα

Αναστοχασμός

  1.    Ποια κορυφή ισοσκελούς τριγώνου βρίσκεται πάνω στον άξονα συμμετρίας του;
  2.    Ένα ορθογώνιο τρίγωνο μπορεί να έχει άξονα συμμετρίας;
  3.    Οι άξονες συμμετρίας ενός ισόπλευρου τριγώνου, τι άλλο είναι στο τρίγωνο;