Καθετότητα - Ύψη τριγώνου

42

Διερεύνηση

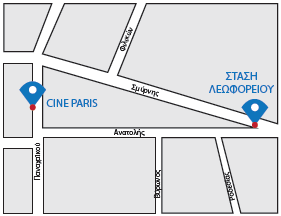
1. Ποια διαδρομή πρέπει να ακολουθήσουν τα παιδιά, για να φτάσουν από τη στάση λεωφορείου στο Cine Paris, διανύοντας τη μικρότερη απόσταση; Την οδό Σμύρνης ή την οδό Ανατολής, αν ο κινηματογράφος απέχει το ίδιο από τις δύο οδούς;

Κάνουμε μία εκτίμηση: ....................
.........................................................

Συζητάμε στην τάξη τις επιλογές μας και καταλήγουμε σε συμπεράσματα για το πώς μετράμε την απόσταση.

2.Βρίσκουμε την απόσταση ενός σημείου Α από μία ευθεία.

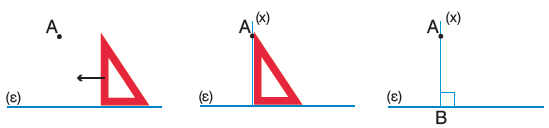
3.Χρησιμοποιούμε τον γνώμονα, για να σχεδιάσουμε τις αποστάσεις από
τις άλλες δύο κορυφές Β και Γ του τριγώνου προς τις απέναντί τους πλευρές.

Συζητάμε στην τάξη τις παρατηρήσεις μας για τα τρία ευθύγραμμα τμήματα που δείχνουν τις αποστάσεις των κορυφών του τριγώνου από τις απέναντί τους πλευρές.

Μικροπείραμα

Καθετότητα - Ύψη τριγώνου

Ενότητα 7

Βασικές μαθηματικές έννοιες και διεργασίες		Παραδείγματα
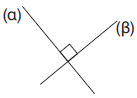
Κάθετες ονομάζονται δύο ευθείες που τέμνονται, έτσι ώστε να σχηματίζουν γωνία 90°. Για να σχεδιάσουμε κάθετες ευθείες, χρησιμοποιούμε τον γνώμονα.		Γράφουμε: α ⊥ β Διαβάζουμε: η ευθεία α είναι κάθετη στην ευθεία β.
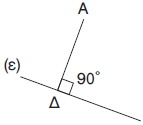
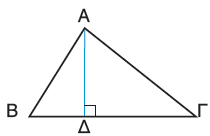
Το ευθύγραμμο τμήμα που ξεκινά από ένα σημείο και τέμνει κάθετα μια ευθεία ονομάζεται απόσταση του σημείου από την ευθεία. Η απόσταση είναι η πιο σύντομη διαδρομή που ενώνει το σημείο με την ευθεία. Σημείωση: Ευθύγραμμο τμήμα είναι ένα τμήμα μιας ευθείας που έχει δύο σημεία για άκρα.		Η απόσταση του σημείου Α από την ευθεία (ε) είναι το ευθύγραμμο τμήμα ΑΔ.
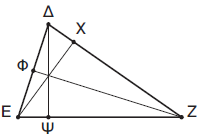
Το ευθύγραμμο τμήμα που ξεκινά από μια κορυφή ενός τριγώνου και είναι κάθετο στην απέναντι πλευρά ονομάζεται ύψος του τριγώνου. Κάθε τρίγωνο έχει τρία ύψη. Τα ύψη ενός τριγώνου διέρχονται από το ίδιο σημείο.		Τρίγωνο ΔΕΖ με τα τρία ύψη ΔΨ, ΕΧ και ΖΦ. ΔΨ ⊥ ΕΖ ΖΦ ⊥ ΔΕ ΕΧ ⊥ ΔΖ

Εφαρμογή

Να κατασκευάσετε τα ύψη στο παρακάτω τρίγωνο ΑΒΓ και να βρείτε το σημείο στο οποίο τέμνονται.

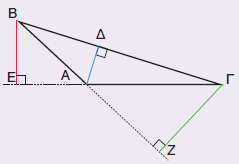
Το τρίγωνο ΑΒΓ είναι αμβλυγώνιο.

Παρατηρούμε ότι, για να φέρουμε το ύψος ΒΕ από την κορυφή Β στην πλευρά ΑΓ, χρειάζεται να προεκτείνουμε την ευθεία πάνω στην οποία βρίσκεται η πλευρά αυτή.

Εργαζόμαστε με τον ίδιο τρόπο, για να φέρουμε και το ύψος ΓΖ από την κορυφή Γ στην πλευρά ΑΒ.

Τα ύψη τέμνονται σε σημείο εκτός του τριγώνου. Προεκτείνουμε και τα τρία ύψη και βρίσκουμε το σημείο στο οποίο τέμνονται.

Αναστοχασμός

Πού βρίσκεται το σημείο όπου συναντιούνται τα τρία ύψη ενός ορθογώνιου τριγώνου;
Πού βρίσκεται το σημείο όπου συναντιούνται τα τρία ύψη ενός αμβλυγώνιου τριγώνου;
Ποια είναι τα δύο ύψη του ορθογώνιου τριγώνου που είναι πάντοτε σχεδιασμένα;