Eίδη τριγώνων ως προς τις πλευρές

41

Διερεύνηση

Κατασκευάζουμε τρίγωνα και συγκρίνουμε τις πλευρές τους και τις γωνίες τους.

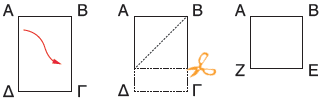
α. Διπλώνουμε μια σελίδα χαρτί μεγέθους Α4, όπως φαίνεται στην εικόνα, έτσι ώστε να σχηματιστεί τετράγωνο.
Έπειτα διπλώνουμε το τετράγωνο με τέτοιον τρόπο, ώστε η κορυφή Ε να συμπέσει με την κορυφή Α.

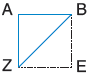
α1. Με δίπλωση συγκρίνουμε τις δύο κάθετες πλευρές του τριγώνου ΑΒΖ.

Οι πλευρές ΑΖ και ΑΒ είναι ………………………….. .

α2. Τι συμπεραίνουμε για τις δύο οξείες γωνίες Α$\widehat{Ζ}$Β και Α$\widehat{Β}$Ζ;

....................................................................................................................................................

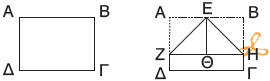
β. Διπλώνουμε μία σελίδα χαρτί μεγέθους Α4, έτσι ώστε η κορυφή Α και η κορυφή Β να συμπέσουν στο σημείο Θ. Κόβουμε τα μέρη που περισσεύουν και έτσι έχουμε το τρίγωνο ΕΖΗ.

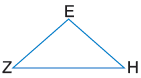
β1. Με δίπλωση συγκρίνουμε τις δύο πλευρές ΕΖ και ΕΗ του τριγώνου ΕΖΗ.

Οι πλευρές ΕΖ και ΕΗ είναι ………………………….. .

β2. Τι συμπεραίνουμε για τις δύο οξείες γωνίες Ε$\widehat{Ζ}$Η και Ε$\widehat{H}$Ζ ;

....................................................................................................................................................

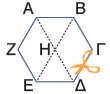
γ. Κόβουμε το εξάγωνο από το παράρτημα. Ενώνουμε με μία ευθεία την κορυφή Α με την κορυφή Δ και την κορυφή Β με την Ε. Σχηματίζεται, έτσι, το τρίγωνο ΕΔΗ.

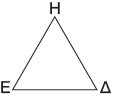
γ1. Με δίπλωση συγκρίνουμε και τις τρεις πλευρές του τριγώνου ΕΔΗ.

Οι πλευρές ΕΗ, ΕΔ και ΔΗ είναι ………………………….. .

γ2. Τι συμπεραίνουμε για τις τρεις οξείες γωνίες του τριγώνου;

....................................................................................................................................................

Συζητάμε στην τάξη ποια είδη τριγώνων μπορούμε να διακρίνουμε με κριτήριο τις πλευρές των τριγώνων.

Eίδη τριγώνων ως προς τις πλευρές

Ενότητα 7

Βασικές μαθηματικές έννοιες και διεργασίες		Παραδείγματα
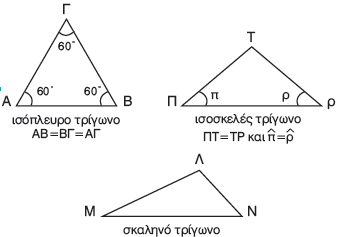
Το τρίγωνο που έχει: και τις τρεις πλευρές του ίσες λέγεται ισόπλευρο, μόνο τις δύο πλευρές του ίσες λέγεται ισοσκελές, όλες τις πλευρές του άνισες λέγεται σκαληνό.
Το ισόπλευρο τρίγωνο έχει και τις τρεις γωνίες του ίσες. Το ισοσκελές τρίγωνο έχει δύο γωνίες ίσες, αυτές που βρίσκονται απέναντι από τις ίσες πλευρές. , Το σκαληνό τρίγωνο έχει και τις τρεις γωνίες άνισες.

Εφαρμογή

1. Να κατασκευάσετε ένα τρίγωνο ΑΔΕ με πλευρά ΑΕ=4εκ. και γωνία $\widehat{A}$= 65° και $\widehat{E}$= 65°.

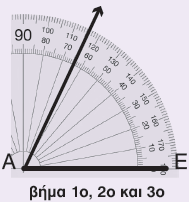
1ο βήμα: Σχεδιάζουμε ένα ευθύγραμμο τμήμα ΑΕ = 4εκ.

2ο βήμα: Τοποθετούμε το κέντρο του μοιρογνωμόνιου στο σημείο Α και την ένδειξη 0 της κλίμακας του μοιρογνωμόνιου που θα χρησιμοποιήσουμε πάνω στην πλευρά ΑΕ και προς τα δεξιά.

3ο βήμα: Βρίσκουμε στην κλίμακα το 65° και βάζουμε μια τελεία. Ενώνουμε την τελεία με το σημείο Α. Σχηματίζουμε με τον τρόπο αυτό μια γωνία 65°.

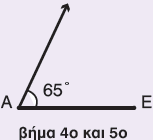
4ο βήμα: Επαναλαμβάνουμε τα βήματα 2 και 3. Κατασκευάζουμε με τον ίδιο τρόπο μία γωνία 65° τοποθετώντας το κέντρο του μοιρογνωμόνιου στο σημείο Ε.

5ο βήμα: Προεκτείνουμε τις δύο πλευρές των γωνιών, μέχρι να συναντηθούν στο σημείο Δ. Με αυτόν τον τρόπο κατασκευάζουμε το τρίγωνο ΑΔΕ.

Αναστοχασμός

Χωρίς να χρησιμοποιήσουμε το μοιρογνωμόνιο, εξηγούμε γιατί κάθε γωνία ισόπλευρου τριγώνου είναι 60°.
Μπορεί ένα σκαληνό τρίγωνο να είναι και αμβλυγώνιο;