Προσανατολισμός στον χώρο

37

Διερεύνηση

1.Το σκάκι είναι ένα επιτραπέζιο παιχνίδι στρατηγικής, το οποίο παίζεται ανάμεσα σε δύο παίκτες. Στους επίσημους αγώνες οι κινήσεις κάθε παρτίδας καταγράφονται.

Προέκυψε επομένως η ανάγκη να μπορεί κανείς να προσδιορίσει με μοναδικό τρόπο κάθε συγκεκριμένη θέση πάνω στη σκακιέρα.

α. Χρησιμοποιώντας το αντίστοιχο γράμμα και αριθμό, προσδιορίζουμε τη θέση του Αξιωματικού λευκού χρώματος πάνω στη σκακιέρα: ...........................................

β. Σε ποια οριζόντια γραμμή και κατακόρυφη στήλη βρίσκεται ο Βασιλιάς μαύρου χρώματος; ..............................................

γ. Ποιο κομμάτι του σκακιού βρίσκεται στη θέση (ζ ,5);
...............................................................................................

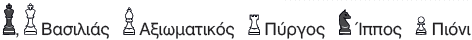
δ. Είναι αρκετό να γνωρίζουμε ότι ο Βασιλιάς λευκού χρώματος βρίσκεται στη γραμμή 8, για να προσδιορίσουμε με μοναδικό τρόπο τη θέση του; Εξηγούμε. …………………….........................

2.Τα παιδιά παίζουν το παιχνίδι του κρυμμένου θησαυρού και
κρατάνε στο χέρι τους έναν χάρτη και τις οδηγίες.

ΟΔΗΓΙΕΣ:Ψάξτε στη ρίζα του δέντρου που είναι 6 τετράγωνα ανατολικά και 3 τετράγωνα βόρεια από το εκκλησάκι.

Σημείωση: πλευρά τετραγώνου = 50 μέτρα.

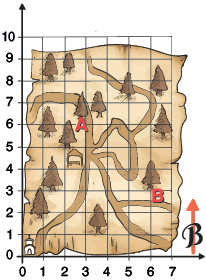
α. Ποιο παιδί έχει δίκιο; .................................

β. Αν γράψουμε το σημείο Β ως (6,3), πώς θα
γράψουμε το σημείο Α; ...................................

γ. Αν ο χάρτης δεν είχε σημείο αναφοράς
το εκκλησάκι αλλά το κιόσκι, τι θα άλλαζε;

......................................................................

Συζητάμε στην τάξη τη βοήθεια που προσφέρουν οι δύο κάθετες αριθμογραμμές και το σημείο αναφοράς, το (0,0), στον προσδιορισμό της θέσης ενός συγκεκριμένου σημείου πάνω στον χάρτη με έναν μοναδικό τρόπο.

Προσανατολισμός στον χώρο

Ενότητα 7

Βασικές μαθηματικές έννοιες και διεργασίες		Παραδείγματα
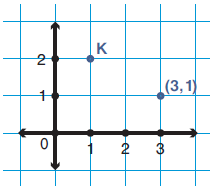
Για τον προσδιορισμό ενός σημείου χρησιμοποιούμε δύο αριθμογραμμές κάθετες μεταξύ τους, μία οριζόντια και μία κατακόρυφη.		Το σημείο Κ είναι το (1,2)
Ο προσδιορισμός της θέσης κάθε σημείου γίνεται με τον συνδυασμό των δύο τιμών οι οποίες δείχνουν πόσο απέχει το σημείο αυτό οριζόντια και κατακόρυφα από τις αριθμογραμμές.
Οι τιμές εξαρτώνται κάθε φορά από το σημείο αναφοράς, δηλαδή το σημείο (0,0).

Εφαρμογή

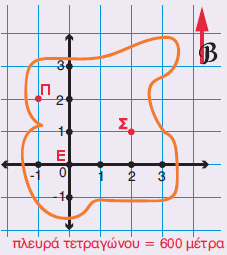
1. Τα παιδιά έχουν κατασκηνώσει στο δάσος. Πώς θα μετακινηθούν από τη σπηλιά (Σ) όπου έστησαν τη σκηνή τους, στην πηγή (Π), για να πάρουν νερό;

α. Τα σημεία Σ και Π απέχουν μεταξύ τους στην οριζόντια αριθμογραμμή 3 τετράγωνα, δηλαδή ………... μέτρα και στην κατακόρυφη 1 τετράγωνο, δηλαδή …….. μέτρα.

β. Ο χάρτης δείχνει τον βορρά. Επομένως, για να πάνε από τη σπηλιά στην πηγή με τη βοήθεια πυξίδας, θα περπατήσουν 600 μέτρα βόρεια και μετά ……..…. μέτρα δυτικά.

2. Τα παιδιά, όταν γύρισαν, είπαν στους συμμαθητές τους ότι κατασκήνωσαν στη θέση (2,1) σε μια σπηλιά. Είχαν δίκιο;

α. Το σημείο Σ, όπου βρίσκεται η σπηλιά, στον χάρτη των παιδιών
είναι …… τετράγωνα ανατολικά από το Ε και ... τετράγωνο βόρεια.
Άρα είναι το σημείο (…,…)

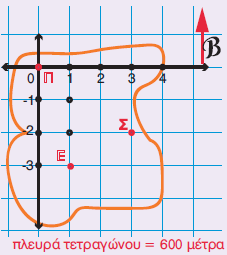
β. Αν όμως τα παιδιά χρησιμοποιούσαν έναν χάρτη, όπως τον διπλανό, με ένα άλλο σημείο αναφοράς, π.χ. την πηγή, τότε το σημείο Σ θα ήταν (3, -2), δηλαδή διαφορετικό.

Άρα η θέση του κάθε σημείου εξαρτάται από το σημείο αναφοράς.

Αναστοχασμός

Σε έναν χάρτη ο οποίος στο πάνω μέρος δείχνει τον βορρά, εξηγούμε ποια πόλη βρίσκεται πιο δυτικά: αυτή που είναι στο σημείο (2,9) ή αυτή που είναι στο σημείο (9,2);