1η Άσκηση ____________________________________________________

Συμπληρώνουμε τους αριθμούς που λείπουν στα παρακάτω αριθμητικά μοτίβα.

α.	0,001	0,01		1	10		1.000

β.	5.000	500	50		0,5		0,005

γ.	18	26	34		50		66

2η Άσκηση ____________________________________________________

Στο παρακάτω μοτίβο ανακαλύπτουμε τον κανόνα και σχεδιάζουμε το επόμενο σχήμα.

3η Άσκηση ____________________________________________________

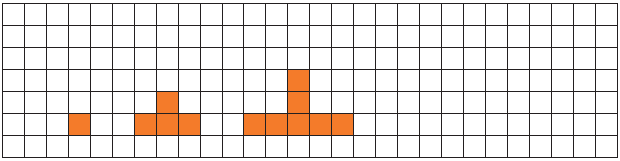
Ποιος αριθμός αντιστοιχεί σε κάθε σχήμα, ώστε να ισχύουν οι παρακάτω ισότητες;

5 + = 30 + 8	3 $\text{☓}$ = 24 - 9	2 $\text{☓}$ = 10 + 6	21 : = 30 - 23
=	=	=	=

1ο Πρόβλημα __________________________________________________

Κατά την επίσκεψή τους σε ένα θέατρο τα παιδιά μετρούσαν το πλήθος των θέσεων του θεάτρου. Παρατήρησαν ότι η πρώτη από τη σκηνή σειρά είχε 30 θέσεις, η δεύτερη σειρά είχε δύο θέσεις περισσότερες από την πρώτη, η τρίτη σειρά 2 θέσεις περισσότερες από τη δεύτερη κ.ο.κ. Όλες οι σειρές ήταν 10. Πόσες θέσεις είχε το θέατρο;

2ο Πρόβλημα __________________________________________________

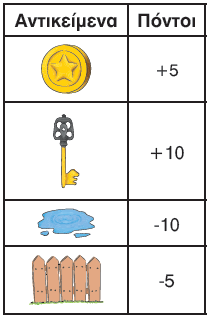
Στον διπλανό πίνακα παρουσιάζονται οι πόντοι τους οποίους κερδίζει ή χάνει ο ήρωας σε ένα ηλεκτρονικό παιχνίδι, όταν αγγίζει καθένα από τα αντικείμενα.
Στην πρώτη πίστα του παιχνιδιού ο ήρωάς μας ξεκινά με 0 πόντους. Στο τέλος της πρώτης πίστας έχει συγκεντρώσει 2 κέρματα, 1 κλειδί και έχει αγγίξει δύο φορές νερό και μία φορά φράχτη.

Πόσους πόντους έχει ο ήρωάς μας στο τέλος της πρώτης πίστας;

Υπολογίζουμε με τη βοήθεια της αριθμογραμμής:

Μικροπείραμα