Ισότητες και ανισότητες

35

Διερεύνηση

1.Παρατηρούμε τα στερεά στις παρακάτω ζυγαριές. Οι δυο ζυγαριές ισορροπούν.

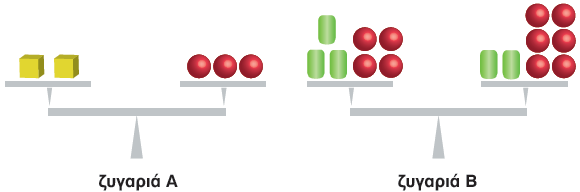
α. Παρατηρούμε τη ζυγαριά Α. Ποιο στερεό ζυγίζει περισσότερο; Ο κύβος ή η σφαίρα; Εξηγούμε την απάντησή μας. ......................................................................................................................

......................................................................................................................................................

β. Παρατηρούμε τη ζυγαριά Β. Ποιο στερεό ζυγίζει περισσότερο; Ο κύλινδρος ή η σφαίρα;
Εξηγούμε την απάντησή μας. ......................................................................................................

......................................................................................................................................................

γ. Πόσο ζυγίζει το κάθε στερεό, αν ο κύλινδρος ζυγίζει 200 γρ. ;

: 200 γρ. : ………………. : ……………….

2.Παρατηρούμε την παρακάτω ζυγαριά.

α. Τοποθετούμε το κατάλληλο σύμβολο (<, >, =) στην παρακάτω σχέση, για να δηλώσουμε ποια στερεά ζυγίζουν περισσότερο.

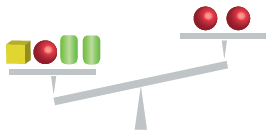
β. Ποια και πόσα στερεά χρειάζεται να προσθέσουμε
ή να αφαιρέσουμε, ώστε η ζυγαριά να ισορροπήσει;

Προτείνουμε δύο τρόπους σχεδιάζοντας τα στερεά σε κάθε μέρος της ζυγαριάς.

Ισότητες και ανισότητες

Ενότητα 6

Βασικές μαθηματικές έννοιες και διεργασίες		Παραδείγματα
Το ίσον (=) είναι το σύμβολο της ισότητας και φανερώνει πως ό,τι βρίσκεται αριστερά του έχει την ίδια αξία (τιμή) με ό,τι βρίσκεται δεξιά του.		5 = 2 $\text{☓}$ 2,5 10 + 2 = 4 $\text{☓}$ 3 18 : ◻ = 7 + 2
Το μεγαλύτερο (>) και το μικρότερο (<) είναι τα σύμβολα της ανισότητας και φανερώνουν πως ό,τι βρίσκεται αριστερά τους είναι μεγαλύτερο ή μικρότερο, αντίστοιχα, από ό,τι βρίσκεται δεξιά τους.		5 < 2 $\text{☓}$ 3,5 4 + 5 > 6 + $\dfrac{2}{5}$ 18 + ◻ < 4 $\text{☓}$ 6

Εφαρμογή

1. Να συμπληρώσετε με τον κατάλληλο αριθμό το κουτάκι στην ισότητα 12 + ⬜ = 4 $\text{☓}$ 5
Στην ισότητα ό,τι βρίσκεται αριστερά από το ίσον έχει την ίδια αξία (τιμή) με ό,τι βρίσκεται δεξιά του.

Δεξιά από το ίσον έχουμε 4 $\text{☓}$ 5 = ………. .
Αριστερά από το ίσον έχουμε 12 + ⬜ = ……. . Επομένως θα συμπληρώσουμε το κουτάκι με τον αριθμό ………. .

2. Να χρησιμοποιήσετε τις ιδιότητες των πράξεων και να συμπληρώσετε τα κουτάκια με τους κατάλληλους αριθμούς. Να εξηγήσετε πώς σκεφτήκατε.

α.   Αν 7 + 8 = 20 - 5, τότε 20 – ⬜ = 7 + 8.
β.   Αν 11 + 6 = 29 – 12 και 29 – 12 = 4 + 13, τότε 11 + 6 = 4 + ⬜.
γ.   (5+7) + ⬜ = 5 + (7 + 4)

3. Να βρείτε τους φυσικούς αριθμούς με τους οποίους μπορείτε να συμπληρώσετε το κουτάκι στην ανισότητα 9 + ⬜ < 23 - 7. Να εξηγήσετε πώς σκεφτήκατε.

Το δεύτερο μέρος της ανισότητας κάνει 23 – 7 = ……... .
Επομένως 9 + ⬜ < …….. .
Άρα μπορούμε να συμπληρώσουμε το ⬜ με έναν από τους αριθμούς:

………. , ………. , ………. , ………. , ………. , ………. , ……….

Αναστοχασμός

Ο Νίκος, για να προσθέσει 3+5+3+1, έγραψε: 3+5=8+3=11+1=12. Αν και βρήκε το σωστό αποτέλεσμα, ποιο είναι το λάθος που έχει κάνει; Εξηγούμε πώς σκεφτήκαμε.
Γράφουμε αριθμούς με τους οποίους μπορούμε να συμπληρώσουμε το ⬜ στην ανισότητα
6+ ⬜ > 10 . Εξηγούμε τη σκέψη μας.