Μαθηματικά (Ε' Δημοτικού) - Βιβλίο Μαθητή (Εμπλουτισμένο)
1.
2. Στον παρακάτω πίνακα καταγράφονται οι απαντήσεις των 200 μαθητών και μαθητριών ενός
δημοτικού σχολείου στα ερωτήματα μιας έρευνας που
πραγματοποιήθηκε στο σχολείο τους.
Τι τρώω για πρωινό; |
|
|---|---|
Απαντήσεις |
Ποσοστό |
γάλα |
45% |
γάλα με δημητριακά |
38% |
χυμός πορτοκαλιού |
17% |
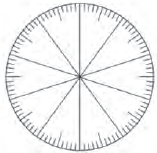
α. Χρωματίζουμε στο κυκλικό
διάγραμμα τα ποσοστά που
εκφράζουν το μέρος των
μαθητών και μαθητριών που
έδωσε την κάθε απάντηση.
β. Βρίσκουμε το πλήθος των μαθητών και μαθητριών που έδωσε την καθεμία απάντηση.
| γάλα | γάλα με δημητριακά | χυμός πορτοκαλιού | |
|---|---|---|---|
| πλήθος μαθητών/ μαθητριών |
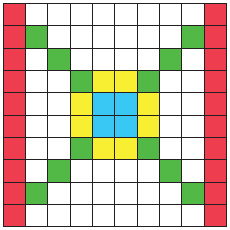
3. Ο Αντρέι, κατά τη διάρκεια της επίσκεψής του σε ένα εργαστήριο ψηφιδωτών, έφτιαξε το τετράγωνο ψηφιδωτό της παρακάτω εικόνας. Εκφράζουμε το μέρος της επιφάνειας του ψηφιδωτού που καλύπτεται με:
| Χρώμα | Με δεκαδικό αριθμό |
Με κλάσμα με παρονομαστή το 100 |
Με ποσοστό στα εκατό (%) |
|---|---|---|---|
| κόκκινο | |||
| πράσινο | |||
| κίτρινο | |||
| μπλε |
| Βασικές μαθηματικές έννοιες και διεργασίες |
|
Παραδείγματα |
| Το ποσοστό εκφράζει το μέρος μιας ποσότητας. Το ποσοστό στα εκατό (%) είναι ένα μέρος από τα 100 ίσα μέρη στα οποία χωρίζουμε την ακέραιη μονάδα. |
|
|
| Το ποσοστό στα εκατό (%) μπορεί να εκφραστεί με δεκαδικό κλάσμα με παρονομαστή το 100 και με δεκαδικό αριθμό. |
|
40% = $\dfrac{40}{100}$ = 0,40 |
| Η ποσότητα που εκφράζει ένα ποσοστό εξαρτάται από την τιμή στην οποία αναφέρεται. |
|
|
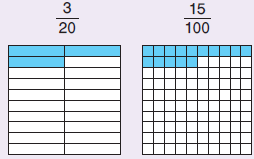
1. Να εκφράσετε με ποσοστό στα εκατό (%) το κλάσμα $\dfrac{3}{20}$.
α΄ τρόπος: Βρίσκουμε ένα κλάσμα ισοδύναμο με το $\dfrac{3}{20}$ με παρονομαστή το 100. Είναι: $\dfrac{3}{20}$ = $\dfrac{3 \text{☓} 5}{20 \text{☓} 5}$ = $\dfrac{15}{100}$ = 15%
β΄ τρόπος: Κάνουμε διαίρεση. Είναι: $\dfrac{3}{20}$ = 3:20 = 0,15 = 15%
2. Ο Νίκος, στην περίοδο των εκπτώσεων, αγόρασε μία μπάλα ποδοσφαίρου με έκπτωση 30%. Η αρχική τιμή της, πριν από την έκπτωση, ήταν 15 €. Πόσα € πλήρωσε;
α΄ τρόπος:
Σκέψη: Η έκπτωση είναι τα $\dfrac{30}{100}$ της αρχική τιμής, δηλαδή είναι τα $\dfrac{30}{100}$ του 15.
Λύση
Υπολογίζουμε την έκπτωση σε €. Είναι $\dfrac{30}{100}$ $\text{☓}$ 15 = $\dfrac{30 \text{☓} 15}{100}$ = $\dfrac{450}{100}$ = 4,50 ή
$\dfrac{30}{100}$ $\text{☓}$ 15 = 0,30 $\text{☓}$ 15= 4,50 ή 15: 100 = 0,15 και 0,15 $\text{☓}$ 30 = 4,50 €
Ο Νίκος πλήρωσε 15 – 4,50 = 10,50 €
β΄ τρόπος:
Σκέψη: Η έκπτωση είναι 30% , δηλαδή ο Νίκος πλήρωσε τα 70 % της αρχικής τιμής.
Λύση
Ο Νίκος πλήρωσε $\dfrac{70}{100}$ $\text{☓}$ 15 = 0,70 $\text{☓}$ 15 = 10,50 € ή $\dfrac{70}{100}$ $\text{☓}$ 15 = $\dfrac{70 \text{☓} 15}{100}$ = $\dfrac{1.050}{100}$ = 10,50 €
ή 15:100 = 0,15 και 0,15 $\text{☓}$ 70= 10,50 €
