Μαθηματικά (Ε' Δημοτικού) - Βιβλίο Μαθητή (Εμπλουτισμένο)

Η διαίρεση στους δεκαδικούς αριθμούς

30

Εικόνα

Διερεύνηση

Εικόνα

1. Υπολογίζουμε το πηλίκο 2,4 : 4.

  • Χρησιμοποιούμε το μοντέλο αναπαράστασης,
    για να βρούμε το πηλίκο 2,4 : 4.
  • Είναι 2,4 : 4 = ………….…. .
Εικόνα

2. Υπολογίζουμε το πηλίκο 3 : 0,6.
α΄ τρόπος: Υπολογίζουμε πόσες φορές χωρά το 0,6
στις 3 ακέραιες μονάδες. Επομένως 3 : 0,6 = …… .
β΄ τρόπος: Κάνουμε την πράξη ακολουθώντας τη συμβουλή του Νίκου.

Εικόνα

3. Η Αγγελική θέλει να μοιράσει εξίσου σε 4 βαζάκια 134 γραμμάρια μαρμελάδας.
Πόσα γραμμάρια μαρμελάδας θα βάλει σε κάθε βαζάκι;

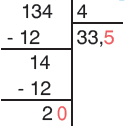
Εικόνα
Εικόνα

Συζητάμε πώς η σκέψη του Νίκου μας οδηγεί
στην κάθετη πράξη.

Εικόνα
Από τον τρόπο του Νίκου ➨ στην κάθετη πράξη της διαίρεσης
4 $\text{☓}$ 30 = 120 μονάδες 30 φορές (3 δεκάδες) χωράει το 4 στο 134.
4 $\text{☓}$ 3 =12 μονάδες 3 φορές (3 μονάδες) χωράει το 4 στο 14.
Το υπόλοιπο είναι 2 μονάδες που τις μετατρέπουμε σε 20 δέκατα. Το υπόλοιπο είναι 2 μονάδες που τις μετατρέπουμε σε 20 δέκατα.
4 $\text{☓}$ 5 = 20 δέκατα 0,5 φορές (5 δέκατα) χωράει το 4 στο 2.
Εικόνα

4. Χρησιμοποιούμε την αριθμομηχανή τσέπης, για να υπολογίσουμε τα πηλίκα:
α. 8,25 : 10 = ………..   β. 82,5 : 100 = …………    γ. 825 : 1.000 = ……………

δ. 8,25 : 0,1 = ………   ε. 82,5 : 0,01 = …………    στ. 825 : 0,001 = ……….…

Η διαίρεση στους δεκαδικούς αριθμούς

Ενότητα 5

Βασικές μαθηματικές έννοιες και διεργασίες

 

 Παραδείγματα
Για να διαιρέσουμε φυσικούς ή δεκαδικούς αριθμούς με φυσικούς ή δεκαδικούς αριθμούς, μπορούμε να εργαστούμε, όπως μάθαμε, με πολλούς τρόπους.

 

 
Σε μια κάθετη διαίρεση φυσικού ή δεκαδικού αριθμού με φυσικό αριθμό:
  1. διαιρούμε τις ακέραιες μονάδες,
  2. μετατρέπουμε το υπόλοιπο σε δέκατα και προσθέτουμε ταυτόχρονα τα δέκατα που μπορεί να έχει ο Διαιρετέος,
  3. βάζουμε υποδιαστολή στο πηλίκο, γιατί μετά διαιρούμε τα δέκατα της ακέραιης μονάδας,
  4. διαιρούμε τα δέκατα της μονάδας,
  5. μετατρέπουμε το νέο υπόλοιπο σε εκατοστά, προσθέτουμε τα εκατοστά που μπορεί να έχει ο Διαιρετέος και συνεχίζουμε τη διαίρεση.

 
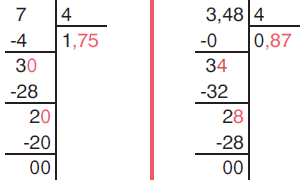
Εικόνα
Στη διαίρεση, αν πολλαπλασιάσουμε Διαιρετέο και διαιρέτη με τον ίδιο αριθμό, το πηλίκο δεν αλλάζει.

 

 3,2 : 0,25 = (3,2x100) : (0,25x100) =
= 320 : 25 = 12,8
Όταν διαιρούμε έναν φυσικό ή δεκαδικό αριθμό με 10, 100, 1.000, ο αριθμός μικραίνει, αντίστοιχα, 10, 100, 1.000 φορές. Επομένως η υποδιαστολή μετακινείται, αντίστοιχα, 1, 2 ή 3 θέσεις αριστερά.

 

 3,4 : 10 = 0,34
3,4 : 100 = 0,034
3 : 1.000 = 0,003
Εικόνα

Εφαρμογή

Να υπολογίσετε το γινόμενο 0,8 x 3,2.

Εικόνα

α΄ τρόπος: Χωρίζουμε τις 2 ακέραιες μονάδες, τα 4 δέκατα
και τα 8 εκατοστά σε ….. ίσα μέρη. Επομένως 2,48 : 4 = …….. .

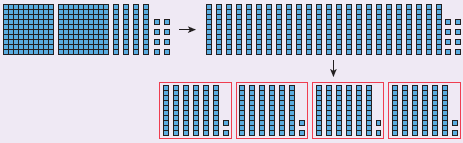
Εικόνα








β΄ τρόπος: Κάνουμε τη διαίρεση κάθετα.

Εικόνα

Αναστοχασμός

  1. Όταν διαιρούμε έναν δεκαδικό ή φυσικό αριθμό με το 0,1 ή το 0,01 ή το 0,001, το πηλίκο είναι
    μικρότερο ή μεγαλύτερο από τον διαιρετέο; Εξηγούμε την απάντησή μας.
  2. Πότε το πηλίκο μιας διαίρεσης είναι μικρότερο από το 1;