Μαθηματικά (Ε' Δημοτικού) - Βιβλίο Μαθητή (Εμπλουτισμένο)

Ο πολλαπλασιασμός στους δεκαδικούς αριθμούς

29

Εικόνα

Διερεύνηση

1. Αξιοποιούμε τις ιδέες των παιδιών και υπολογίζουμε το γινόμενο 0,8 x 0,4 με διαφορετικούς τρόπους:

Εικόνα
  1. Μετατρέπουμε τους δεκαδικούς αριθμούς σε κλάσματα.
    0,8 $\text{☓}$ 0,4 = $\dfrac{◻}{◻}$ $\text{☓}$ $\dfrac{◻}{◻}$ = $\dfrac{◻}{◻}$ = …….
  • Συζητάμε αν το γινόμενο θα είναι ίδιο αλλάζοντας τη
    σειρά των παραγόντων.

  1. Χρησιμοποιούμε μοντέλα αναπαράστασης
Εικόνα


  • Χρησιμοποιούμε το παραπάνω μοντέλο αναπαράστασης και χρωματίζουμε τα μέρη της ακέραιης μονάδας, για να βρούμε το γινόμενο 0,8 $\text{☓}$ 0,4. Είναι: 0,8 $\text{☓}$ 0,4 = ………….….

  1. Κάνουμε την πράξη κάθετα
Εικόνα
  • Υπολογίζουμε στο τετράδιό μας με κάθετη πράξη το γινόμενο 3,4 $\text{☓}$ 1,06 και χρησιμοποιούμε τους παραπάνω τρόπους, για να βάλουμε την υποδιαστολή.


Εικόνα

Περιγράφουμε όλες τις παραπάνω στρατηγικές που χρησιμοποιήσαμε.

2. Χρησιμοποιούμε την αριθμομηχανή τσέπης, για να υπολογίσουμε τα γινόμενα:

Εικόνα

α. 2,85 $\text{☓}$ 10 = ……...…     β. 2,85 $\text{☓}$ 100 = ….…..     γ. 2,85 $\text{☓}$ 1.000 = …...……

δ. 2,85 $\text{☓}$ 0,1 = …..……    ε. 2,85 $\text{☓}$ 0,01 = …....…    στ. 2,85 $\text{☓}$ 0,001 = …..……

Εικόνα

Τι συνέβη στον δεκαδικό αριθμό, όταν τον πολλαπλασιάσαμε με τους παραπάνω αριθμούς; Γιατί;

Ο πολλαπλασιασμός στους δεκαδικούς αριθμούς

Ενότητα 5

Βασικές μαθηματικές έννοιες και διεργασίες

 

 Παραδείγματα
Όταν πολλαπλασιάζουμε δεκαδικούς αριθμούς ή δεκαδικό αριθμό με φυσικό αριθμό:
  1. Κάνουμε εκτίμηση του γινομένου.
  2. Κάνουμε την πράξη κάθετα, σαν να ήταν οι παράγοντες φυσικοί αριθμοί, και έπειτα τοποθετούμε την υποδιαστολή στη σωστή θέση.
  3. Ελέγχουμε το γινόμενο με βάση την εκτίμησή μας.

 

 4,16 $\text{☓}$ 3,2 =
α. Κάνω εκτίμηση: 4 $\text{☓}$ 3=12
β. Υπολογίζω:
4,16 $\text{☓}$ 3,2=13,312
γ. Ελέγχω: To 13,312 είναι
κοντά στο 12.
Εικόνα
Στον πολλαπλασιασμό, αν αλλάξουμε τη σειρά των παραγόντων, δεν αλλάζει το αποτέλεσμα.

 

 4,16 $\text{☓}$ 3,2 $\text{☓}$ 1,2 = 3,2 $\text{☓}$ 1,2 $\text{☓}$ 4,16 = 13,312
Όταν πολλαπλασιάζουμε έναν δεκαδικό αριθμό με 10, 100, 1.000, ο αριθμός μεγαλώνει 10, 100, 1.000 φορές αντίστοιχα. Επομένως η υποδιαστολή μετακινείται 1, 2 ή 3 θέσεις δεξιά αντίστοιχα.

 

 10 $\text{☓}$ 3,4 = 34
100 $\text{☓}$ 3,4 = 340 (συμπληρώνω ένα μηδενικό).
Εικόνα

Εφαρμογή

Να υπολογίσετε το γινόμενο 0,8 $\text{☓}$ 3,2.
α. Κάνουμε εκτίμηση του αποτελέσματος: 0,8 $\text{☓}$ 3,2 είναι περίπου 1 $\text{☓}$ 3 = 3.
β. Υπολογίζουμε ακριβώς:
α΄ τρόπος: 0,8 $\text{☓}$ 3,2 = $\dfrac{8}{10}$ $\text{☓} $ $\dfrac{32}{10}$ = $\dfrac{8 ​ \text{☓} ​ 32}{100}$ = $\dfrac{256}{100}$ = …………
β΄ τρόπος:Χρησιμοποιούμε μοντέλα αναπαράστασης.

Εικόνα

                 γ΄ τρόπος:
    Κάνουμε την πράξη κάθετα.

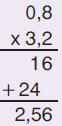
Εικόνα

Το τετράγωνο αναπαριστά την ακέραιη μονάδα.
Ζωγραφίζουμε με κίτρινο χρώμα το 3,2. Μετά με πράσινο χρώμα
ζωγραφίζουμε το 0,8 από το 3,2. Μετράμε και αναδιατάσσουμε τα
πράσινα τετραγωνάκια. Με τον παραπάνω τρόπο αναπαραστήσαμε
τον δεκαδικό αριθμό 2,56.
γ. Ελέγχουμε το αποτέλεσμα: To 2,56 είναι κοντά στο 3.

Μικροπείραμα μικροπείραμα

Εικόνα

Αναστοχασμός

  1. Ποιος αριθμός προκύπτει, αν πολλαπλασιάσουμε τον αριθμό 2,5 με 10 εκατοστά;
  2. Όταν πολλαπλασιάζουμε δυο δεκαδικούς αριθμούς μικρότερους από το 1, το γινόμενό τους είναι μικρότερο από τον κάθε αριθμό ξεχωριστά. Εξηγούμε γιατί συμβαίνει αυτό.