1. Συχνά στην καθημερινή ζωή κάνουμε εκτιμήσεις για διάφορες καταστάσεις.

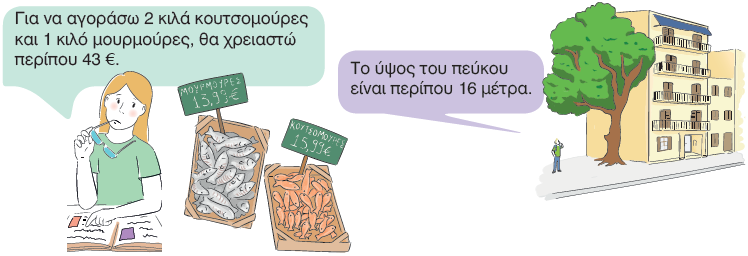
α. Υπολόγισε σωστά η Αγγελική τα χρήματα που θα χρειαστεί, για να αγοράσει ψάρια;
Γιατί πολλοί έμποροι δίνουν στα προϊόντα τους τιμές που τελειώνουν σε 0,99;

β. Τι νομίζετε ότι έλαβε υπόψη του ο Νίκος, για να εκτιμήσει το ύψος του πεύκου;

2.

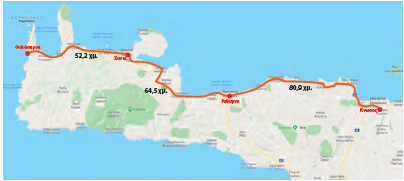
α. Σε ποιο ψηφίο στρογγυλοποίησε τους αριθμούς η
Δανάη; ........................................................................

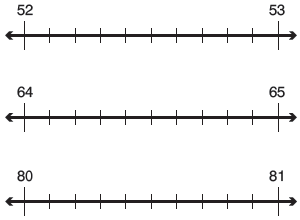
β. Τοποθετούμε τους δεκαδικούς αριθμούς που δείχνουν τις χιλιομετρικές αποστάσεις στις διπλανές αριθμογραμμές. Σε ποιον φυσικό αριθμό είναι κάθε δεκαδικός αριθμός πιο κοντά;

Στρογγυλοποιούμε τους δεκαδικούς αριθμούς με τη βοήθεια των αριθμογραμμών. Εξηγούμε τη σκέψη μας.

...................................................................................

...................................................................................

.........................................................................................................................................................................

Βασικές μαθηματικές έννοιες και διεργασίες		Παραδείγματα
Η εκτίμηση είναι ένα χρήσιμο εργαλείο στην καθημερινή ζωή, γιατί μας δίνει τη δυνατότητα να υπολογίζουμε κατά προσέγγιση διάφορα μεγέθη.		Το μήκος του μολυβιού είναι περίπου 8 εκ. Το ταξίδι θα διαρκέσει περίπου 2,5 ώρες. Το γινόμενο 7,99 x 2,47 είναι περίπου 8 x 2,5 = 20.
Η στρογγυλοποίηση στους δεκαδικούς αριθμούς γίνεται όπως και στους φυσικούς αριθμούς. Προσδιορίζουμε τη θέση του ψηφίου του αριθμού στην οποία θα κάνουμε τη στρογγυλοποίηση. Εξετάζουμε το ψηφίο που βρίσκεται στην αμέσως επόμενη δεξιά θέση. Αν είναι: ► 0, 1, 2, 3 ή 4, τότε αντικαθιστούμε το ψηφίο αυτό και όλα όσα είναι δεξιά του με το 0. ► 5, 6, 7, 8 ή 9, τότε αντικαθιστούμε το ψηφίο αυτό και όλα όσα είναι δεξιά του με το 0 και αυξάνουμε κατά μία μονάδα το ψηφίο της θέσης στην οποία κάνουμε τη στρογγυλοποίηση.		Στρογγυλοποιούμε στα δέκατα τους αριθμούς: α. 23,846     β. 23,876. Στην αμέσως επόμενη δεξιά θέση από το 8 είναι το 4. Τα ψηφία 4, 6 θα αντικατασταθούν με 0. Ο αριθμός θα γίνει: 23,800 ή 23,8. Στην αμέσως επόμενη δεξιά θέση από το 8 είναι το 7. Το ψηφίο 8 στα δέκατα θα αντικατασταθεί με το 9 και τα ψηφία 7, 6 θα αντικατασταθούν με το ψηφίο 0. Ο αριθμός θα γίνει: 23,900 ή 23,9.