Ο Έλληνας Ολυμπιονίκης Λευτέρης Πετρούνιας αναδείχτηκε Παγκόσμιος Πρωταθλητής στο άθλημα των κρίκων στις 7/10/2017 στο Μόντρεαλ του Καναδά. Στον πίνακα αναγράφονται οι επιδόσεις των έξι πρώτων αθλητών κατά τη σειρά με την οποία αγωνίστηκαν:

Χώρα	Αθλητής	Βαθμολογία
Ουκρανία	Ραντιβίλοφ	14,933
Τουρκία	Τσολάκ	15,066
Ρωσία	Αμπλιάζιν	15,333
Γαλλία	Αΐτ Σαΐντ	15,258
Ελλάδα	Πετρούνιας	15,433
Κίνα	Λιου	15,266

α. Παρατηρούμε τον πίνακα και απαντάμε στις παρακάτω ερωτήσεις:

1. Ποιος αθλητής πήρε την υψηλότερη βαθμολογία; ........................................................................................
2. Ποιος αθλητής πήρε τη χαμηλότερη βαθμολογία; ........................................................................................
3. Ποιος αθλητής έχει βαθμολογία κοντά στο 15 $\dfrac{1}{2}$; ........................................................................................

β. Τοποθετούμε τους παραπάνω αριθμούς στον πίνακα αξίας θέσης:

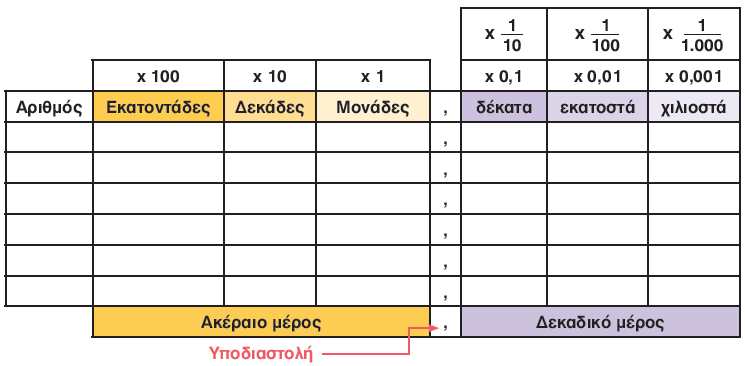
γ. Αναλύουμε τον αριθμό 15,258:
15,258 = (1 $\text{☓}$ 10) + (5 $\text{☓}$ 1) + (2 $\text{☓}$ ……) + (5 $\text{☓}$ ……..) + (…… $\text{☓}$ 0,001) ή
15,258 = (1 $\text{☓}$ 10) + (5 $\text{☓}$ 1) + (….. $\text{☓}$ $\dfrac{1}{10}$ ) + (…… $\text{☓}$ $\dfrac{1}{100}$ ) + (8 $\text{☓}$ ………)

Στο δεκαδικό μέρος ποιο ψηφίο έχει τη μεγαλύτερη αξία; ……………………………………

δ. Γράφουμε σε σειρά τους παραπάνω αριθμούς του πίνακα από τον μικρότερο στον μεγαλύτερο:

............................................. < ............................................. < ............................................ <

............................................. < ............................................. < ............................................

Βασικές μαθηματικές έννοιες και διεργασίες		Παραδείγματα
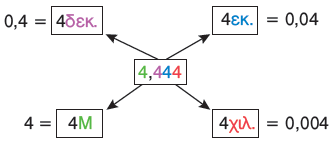
Σε έναν δεκαδικό αριθμό κάθε ψηφίο, ανάλογα με τη θέση του στον αριθμό, έχει διαφορετική αξία.
Μπορούμε να γράψουμε έναν δεκαδικό αριθμό: α. με ψηφία,        β. με λέξεις.		α. 32,006 β. τριάντα δύο και έξι χιλιοστά
Οι δεκαδικοί αριθμοί, όπως και οι φυσικοί, μπορούν να αναλυθούν με το δεκαδικό τους ανάπτυγμα.		3,315 = 3 Μ + 3 δεκ. + 1 εκ. + 5 χιλ. = = (3 x1) + (3 x 0,1) + (1 x 0,01) + (5 x 0,001)
Ανάμεσα σε δύο δεκαδικούς αριθμούς μεγαλύτερος είναι αυτός που έχει μεγαλύτερο ακέραιο μέρος.		26,5 > 24,998        (γιατί 26 > 24)
Για να συγκρίνουμε δύο δεκαδικούς αριθμούς με το ίδιο ακέραιο μέρος, συγκρίνουμε το δεκαδικό τους μέρος, πρώτα τα δέκατα, μετά τα εκατοστά κ.λπ.		Συγκρίνω:    19,76    και    19,7499 ίδιο ακέραιο μέρος (19 =19), ίδια δέκατα (7=7), διαφορετικά εκατοστά ( 6 > 4), άρα 19,76 > 19,7499.

Μικροπείραμα