Δεκαδικά κλάσματα – Δεκαδικοί αριθμοί

25

Διερεύνηση

1. Ο Σύλλογος Γονέων και Κηδεμόνων ενός Δημοτικού Σχολείου έβαψε με πράσινο χρώμα μέρος ενός τοίχου του σχολείου.

α.Αναπαριστάνουμε με ένα τετράγωνο τον τοίχο, όπως φαίνεται στο διπλανό σχήμα. Εκφράζουμε το μέρος της επιφάνειας του τοίχου που καλύφθηκε με πράσινο χρώμα με:

δεκαδικό κλάσμα: $\dfrac{◻}{10}$ ή $\dfrac{◻}{◻}$

δεκαδικό αριθμό: ……… ή ………

β. Παρατηρούμε με τον μεγεθυντικό φακό το τετράγωνο που αναπαριστάνει τον τοίχο. Κάθε τετραγωνάκι του είναι χωρισμένο σε …… ίσα μέρη και επομένως η ακέραιη μονάδα είναι χωρισμένη σε ……………. ίσα μέρη. Εκφράζουμε το μέρος της επιφάνειας του τοίχου που καλύφθηκε με πράσινο χρώμα με:

δεκαδικό κλάσμα: $\dfrac{.....}{1.000}$ δεκαδικό αριθμό: …………

2. Ο Σύλλογος Γονέων και Κηδεμόνων στη συνέχεια χρωμάτισε τη διπλάσια επιφάνεια.

α. Χρωματίζουμε το μέρος της επιφάνειας του τοίχου που καλύφθηκε με πράσινο χρώμα και το εκφράζουμε με:

δεκαδικό κλάσμα	δεκαδικό αριθμό
$\dfrac{.....}{.....}$ ή $\dfrac{.....}{.....}$ ή $\dfrac{.....}{.....}$	..... ή ..... ή .....

β. Εκφράζουμε τα παραπάνω δεκαδικά κλάσματα και δεκαδικούς αριθμούς με μεικτό αριθμό:

………………………………………….………………………………………

γ. Τοποθετούμε τους αριθμούς $\dfrac{16}{10}$ , $\dfrac{8}{10}$, 0,8 και 1,6 στην αριθμογραμμή.

Συζητάμε τον τρόπο με τον οποίο μετατρέπουμε τα δεκαδικά κλάσματα σε δεκαδικούς αριθμούς και το αντίστροφο.

Δεκαδικά κλάσματα – Δεκαδικοί αριθμοί

Ενότητα 5

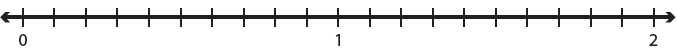
Βασικές μαθηματικές έννοιες και διεργασίες		Παραδείγματα
H ακέραιη μονάδα μπορεί να χωριστεί σε 10, 100, 1.000 ίσα μέρη κ.λπ. Τα δέκατα, τα εκατοστά και τα χιλιοστά της μονάδας μπορούμε να τα γράψουμε με κλάσμα ή δεκαδικό αριθμό.		ένα δέκατο: $\dfrac{1}{10}$ ή 0,1 ένα εκατοστό: $\dfrac{1}{100}$ ή 0,01 ένα χιλιοστό$\dfrac{1}{1.000}$ ή 0,001 1 = 10 δεκ. = 100 εκ. = 1.000 χιλ.
Τα κλάσματα που έχουν παρονομαστή το 10, 100, 1.000 κ.λπ. ονομάζονται δεκαδικά κλάσματα και μπορούν να γραφτούν και με τη μορφή δεκαδικών αριθμών και το αντίστροφο.		$\dfrac{4}{10}$ = 0,4 $\dfrac{32}{100}$ = 0,32 $\dfrac{583}{100}$ = 5,83
		0,543 = $\dfrac{543}{1.000}$ 1,2 = $\dfrac{12}{10}$ 3,31 = $\dfrac{331}{100}$
Οι δεκαδικοί αριθμοί έχουν δύο μέρη, ακέραιο και δεκαδικό, που χωρίζονται με υποδιαστολή. Το ακέραιο μέρος δείχνει τις ακέραιες μονάδες. Το δεκαδικό μέρος δείχνει μέρη της ακέραιης μονάδας. Στο δεκαδικό μέρος τα ψηφία είναι: 1 αν έχω χωρίσει την ακέραιη μονάδα σε 10 ίσα μέρη, 2 αν έχω χωρίσει σε 100, 3 αν έχω χωρίσει σε 1.000 κ.λπ.		38 ακέραιες μονάδες και 57 εκατοστά της ακέραιης μονάδας.
Ο δεκαδικός αριθμός μπορεί να γραφτεί και με τη μορφή μεικτού αριθμού.		38,57 = $\dfrac{3857}{100}$ ή 38,57 = 38$\dfrac{57}{100}$

Εφαρμογή Μετατροπή κλάσματος σε δεκαδικό αριθμό και αντίστροφα

1. Να μετατρέψετε τα κλάσματα $\dfrac{3}{20}$ και $\dfrac{14}{5}$ σε δεκαδικούς αριθμούς.

Μετατρέπουμε σε ισοδύναμα δεκαδικά κλάσματα και έπειτα σε δεκαδικούς αριθμούς.
α. $\dfrac{3}{20}$ = $\dfrac{3 \text{☓} 5} {20 \text{☓} 5}$ = $\dfrac{15}{100}$. Επομένως $\dfrac{3}{20}$ = $\dfrac{15}{100}$ = ..........
β. $\dfrac{14}{5}$ = $\dfrac{14 \text{☓} 2}{5 \text{☓} 2}$ = $\dfrac{28}{10}$ = $\dfrac{20}{10}$ + $\dfrac{8}{10}$ = 2 $\dfrac{8}{10}$ = 2,8 ή $\dfrac{14}{5}$ = $\dfrac{5}{5}$ + $\dfrac{5}{5}$ + $\dfrac{4}{5}$ = 2 $\dfrac{4}{5}$ = 2 $\dfrac{4 \text{☓} 2}{5 \text{☓} 2}$ = 2 $\dfrac{8}{10}$ = ……

2. Να μετατρέψετε τους δεκαδικούς αριθμούς 0,8 και 1,45 σε κλάσματα ή μεικτούς.
Μετατρέπουμε τους δεκαδικούς αριθμούς σε δεκαδικά κλάσματα και έπειτα τα δεκαδικά κλάσματα σε ισοδύναμα ανάγωγα κλάσματα.
α. 0,8 = $\dfrac{8}{10}$ = $\dfrac{8:2}{10:2}$ = $\text{—}$. β. 1,45 = $\dfrac{145}{100}$ = $\dfrac{100}{100}$ + $\dfrac{45}{100}$ = 1 + $\dfrac{45}{100}$ = 1 + $\dfrac{45 : 5}{100 : 5}$ = 1 $\dfrac{9}{20}$ ή $\text{—}$

Αναστοχασμός

Σε έναν δεκαδικό αριθμό μικρότερο της ακέραιης μονάδας, ποιο είναι το ακέραιο μέρος;
Πώς μπορούμε να γράψουμε έναν φυσικό αριθμό με τη μορφή δεκαδικού αριθμού;
Πόσα δέκατα είναι ο δεκαδικός αριθμός 2,4; Πόσα εκατοστά είναι ο ίδιος αριθμός;