Μαθηματικά (Ε' Δημοτικού) - Βιβλίο Μαθητή (Εμπλουτισμένο)

Πιθανότητες

24

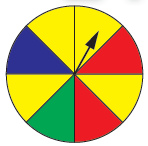
Εικόνα

Διερεύνηση

Εικόνα

Παίζουμε ένα παιχνίδι στο οποίο κερδίζει μόνον όποιος φέρει στον διπλανό τροχό το χρώμα που έχει επιλέξει. Ποιο χρώμα θα διάλεγες για εσένα;

α. Κάνουμε προβλέψεις για το πείραμα τύχης.


Εικόνα

Συζητάμε πόσο πιθανό είναι να έρθει καθένα από τα
χρώματα, αν περιστρέψουμε τον τροχό.

Αποτελέσματα της ομάδας μου
Χρώμα Καταμέτρηση με γραμμές Συχνότητα εμφάνισης με αριθμό
πράσινο    
κίτρινο    
μπλε    
κόκκινο    

β. Κάνουμε το πείραμα τύχης.

Χωριζόμαστε σε ομάδες και χρησιμοποιούμε τον τροχό από το παράρτημα. Περιστρέφουμε τον τροχό 20 φορές και καταγράφουμε τα αποτελέσματά μας.

1. Παρατηρούμε τη συχνότητα εμφάνισης κάθε χρώματος. Ποιο χρώμα είναι πιο πιθανόν να εμφανίζεται κάθε φορά;

.................................................................




Εικόνα
Εικόνα









2. Πόσες φορές αναμένουμε να εμφανιστεί κόκκινο χρώμα σε 8 περιστροφές του τροχού;

...........................................................................................................................................................

3. Πόσες φορές αναμένουμε να εμφανιστεί πράσινο χρώμα σε 8 περιστροφές του τροχού;

...........................................................................................................................................................

γ. Γράφουμε με κλάσμα την πιθανότητα εμφάνισης κάθε χρώματος, όταν περιστρέφουμε τον τροχό.

Πιθανότητα να έρθει: κίτρινο = $\dfrac{◻}{◻}$ , κόκκινο = $\dfrac{◻}{◻}$ , μπλε = $\dfrac{◻}{◻}$ , πράσινο = $\dfrac{◻}{◻}$

Εικόνα

δ. Τοποθετούμε τα κλάσματα στην παρακάτω κλίμακα.

Εικόνα





Εικόνα

Συγκρίνουμε τις πιθανότητες που υπολογίσαμε, με τον τρόπο αυτό, με τις αρχικές μας προβλέψεις.

Πιθανότητες

Ενότητα 4

Βασικές μαθηματικές έννοιες και διεργασίες

 

 Παραδείγματα
Ένα πείραμα που δεν μπορούμε να προβλέψουμε με βεβαιότητα το αποτέλεσμά του, όταν το κάνουμε, ονομάζεται πείραμα τύχης.

 

 Αν ρίξουμε ένα ζάρι 1000 φορές, δεν μπορούμε να προβλέψουμε πόσες φορές θα εμφανιστεί κάθε αριθμός.
Σε ένα πείραμα τύχης, το πόσο πιθανό είναι να έρθει ένα συγκεκριμένο αποτέλεσμα λέγεται πιθανότητα και μπορεί να υπολογιστεί με ένα κλάσμα:
πιθανότητα = $\dfrac{\textbf{πλήθος ​ των ​ επιθυμητών ​ αποτελεσμάτων}}{\textbf{πλήθος ​ των ​ δυνατών ​ αποτελεσμάτων}}$

 

 Η πιθανότητα να έρθει 3, αν ρίξουμε ένα ζάρι είναι:

$\dfrac{πόσες ​ φορές ​ το ​ 3 ​ στο ​ ζάρι}{πλήθος ​ των ​ αριθμών ​ στο ​ ζάρι}$ = $\dfrac{1}{6}$
Η πιθανότητα να έρθει ένα συγκεκριμένο αποτέλεσμα μπορεί να εκφραστεί με μια κλίμακα που εκτείνεται από το αδύνατο να συμβεί έως το βέβαιο ότι θα συμβεί. H μέση της κλίμακας αντιπροσωπεύει αυτό που είναι πιθανό τόσο να συμβεί, όσο και να μην συμβεί.

 

 Όλα τα δυνατά αποτελέσματα είναι 6 (1, 2, 3, 4, 5, 6). Το πλήθος των επιθυμητών απο-τελεσμάτων είναι 1 (το 3 εμφανίζεται μία φορά στα 6 αποτελέσματα).
Εικόνα
Εικόνα

Εφαρμογή Εκφράζω την πιθανότητα με κλάσμα

Μέσα σε μια τσάντα βρίσκονται ανακατεμένες ομοιόμορφες μπάλες. Οι 5 είναι κόκκινες, οι 2 κίτρινες και 3 είναι μπλε. .

α. Υπολογίζουμε την πιθανότητα να τραβήξουμε:

1. μια κίτρινη μπάλα: $\dfrac{\sf{πλήθος ​ ​ από ​ ​ κίτρινες ​ ​ μπάλες}}{\sf{πλήθος ​ ​ από ​ ​ όλες ​ ​ τις​ ​ μπάλες}}$ = $\dfrac{2}{10}$

2. μια κόκκινη μπάλα: $\dfrac{\sf{πλήθος ​ ​ από ​ ​ κόκκινες ​ ​ μπάλες}}{\sf{πλήθος ​ ​ από ​ ​ όλες ​ ​ τις​ ​ μπάλες}}$ = $\dfrac{5}{10}$ = $\dfrac{1}{2}$ (μισές – μισές πιθανότητες).

3. μια πράσινη μπάλα: $\dfrac{\sf{πλήθος ​ ​ από ​ ​ πράσινες ​ ​ μπάλες}}{\sf{πλήθος ​ ​ από ​ ​ όλες ​ ​ τις​ ​ μπάλες}}$ = $\dfrac{0}{10}$ = 0. Η πιθανότητα είναι 0, δηλαδή είναι αδύνατο να συμβεί, γιατί δεν υπάρχει πράσινη μπάλα.

4. μια κόκκινη ή κίτρινη ή μπλε μπάλα:

$\dfrac{\sf{πλήθος ​ ​ από ​ ​ κόκκινες ​ ​ και ​ ​ κίτρινες ​ ​ και ​ ​ μπλε ​ ​ μπάλες}}{\sf{πλήθος ​ ​ από ​ ​ όλες ​ ​ τις​ ​ μπάλες}}$ = $\dfrac{(5+2+3)}{10}$ = $\dfrac{10}{10}$ = 1.

Η πιθανότητα είναι 1, δηλαδή είναι βέβαιο ότι θα συμβεί, γιατί οι μπάλες στην τσάντα είναι μόνο κόκκινες, κίτρινες και μπλε.

β. Τοποθετούμε τις παραπάνω πιθανότητες στην παρακάτω αριθμογραμμή.

Εικόνα
Εικόνα

Αναστοχασμός

  1. Ο Νίκος ισχυρίζεται ότι σε ένα παιχνίδι τύχης με αριθμούς από το 1 έως το 20, το 17 είναι πιο πιθανό να εμφανιστεί, επειδή είναι ο τυχερός του αριθμός. Έχει δίκιο;
  2. Ρίχνουμε ένα ζάρι 10.000 φορές. Πόσες περίπου φορές θα έρθει ο αριθμός 2;