Χαρακτηριστικές τιμές δεδομένων – Mέση τιμή

23

Διερεύνηση

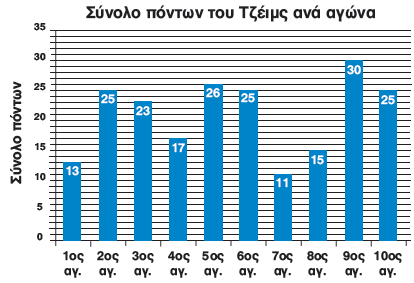
Ο Τζέιμς σημείωσε
στους δέκα πρώτους
αγώνες μπάσκετ της
ομάδας του τους πόντους
που φαίνονται στο
ραβδόγραμμα:

Παρατηρούμε το ραβδόγραμμα:

1. Πόσους πόντους σημείωσε συνολικά και στους δέκα αγώνες;

…………………………..…………

2. Αν οι συνολικοί πόντοι μοιράζονταν εξίσου και στους 10 αγώνες, πόσους πόντους θα σημείωνε σε κάθε αγώνα;

.........................................................................................................................................................

3. Χαράζουμε μια κόκκινη γραμμή παράλληλη στον οριζόντιο άξονα, που θα δείχνει το ύψος των ράβδων, εάν οι συνολικοί πόντοι μοιράζονταν εξίσου και στους 10 αγώνες.

Συμπληρώνουμε τον ακόλουθο πίνακα συχνοτήτων.

Σύνολο διαφορετικών πόντων ανά αγώνα	Καταμέτρηση με γραμμές	Συχνότητα εμφάνισης
13		1

1 Ποια είναι η μικρότερη τιμή πόντων; ....................

2. Ποια είναι η μεγαλύτερη τιμή πόντων; ................

3. Ποια τιμή πόντων εμφανίζεται πιο συχνά; ..........

Διατάσσουμε τους πόντους με τη σειρά από τους λιγότερους, ανά αγώνα, στους περισσότερους.

……………………………...............…………………

Ποια τιμή ή ποιες δύο τιμές βρίσκονται στη μέση της διάταξης και χωρίζουν το σύνολο των τιμών σε δυο ίσα μέρη, από τα οποία το ένα μέρος έχει τις μικρότερες τιμές και το άλλο τις μεγαλύτερες;

............................................................................................................................................................

Συζητάμε και κάνουμε προβλέψεις για το μέλλον του παίκτη.

Με βάση τα δεδομένα, ποια πρόβλεψη μπορούμε να κάνουμε για την πορεία του παίκτη στη διάρκεια της αγωνιστικής περιόδου;
Ποιοι πιθανοί παράγοντες μπορούν να ανατρέψουν τις προβλέψεις μας;

Χαρακτηριστικές τιμές δεδομένων – Mέση τιμή

Ενότητα 4

Βασικές μαθηματικές έννοιες και διεργασίες		Παραδείγματα
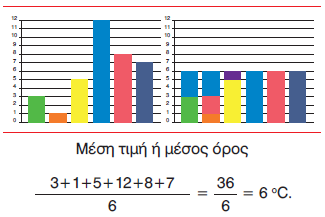
Κατά την επεξεργασία των αριθμητικών δεδομένων, βρίσκουμε κάποιες χαρακτηριστικές τιμές, χρήσιμες στην ερμηνεία των δεδομένων. Μία από αυτές είναι η μέση τιμή ή μέσος όρος.		Οι μετρήσεις της θερμοκρασίας στη Λαμία κάθε 4 ώρες στις 25/12/2017 ήταν: 3 °C, 1 °C, 5 °C, 12 °C, 8 °C, 7 °C.
Για να υπολογίσουμε τη μέση τιμή ή τον μέσο όρο, προσθέτουμε τις τιμές όλων των δεδομένων και διαιρούμε το άθροισμά τους με το πλήθος των δεδομένων. Μέση τιμή ή μέσος όρος = $\dfrac{\textbf{άθροισμα δεδομένων}}{\textbf{πλήθος δεδομένων}}$

Εφαρμογή Υπολογίζω τη μέση τιμή

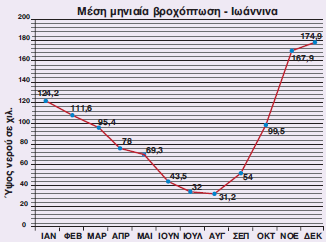
Σύμφωνα με το Εθνικό Αστεροσκοπείο Αθηνών, η μέση μηνιαία βροχόπτωση στην Αθήνα τον περασμένο αιώνα ήταν 33,29 χιλιοστά. Συγκρίνουμε τη μέση μηνιαία βροχόπτωση της Αθήνας με αυτήν της πόλης των Ιωαννίνων την ίδια περίοδο.
Παρατηρούμε και σχολιάζουμε το διάγραμμα.

1. Άθροισμα των δεδομένων:
124,2 +111,6 + 95,4 + 78 + 69,3 + 43,5 + 32 + 31,2 + 54 + 99,5 + 167,9 + 174,9 = 1081,5.

2. Πλήθος των δεδομένων: 12.

3. Άρα η μέση τιμή είναι:

$\dfrac{1081,5}{12}$ = 1081,5 : 12 = 90,125 χιλ.

Παρατηρούμε ότι η μέση μηνιαία βροχόπτωση στα Ιωάννινα είναι σχεδόν τριπλάσια από αυτήν της Αθήνας.

Η μέση τιμή της βροχόπτωσης το καλοκαίρι στα Ιωάννινα είναι περίπου όση είναι η μέση μηνιαία τιμή όλου του έτους για την Αθήνα.

Μικροπείραμα Μικροπείραμα Μικροπείραμα

Αναστοχασμός

Η μέση τιμή ενός συνόλου δεδομένων είναι πάντα η τιμή ενός από τα δεδομένα;
Αν γνωρίζουμε τη μέση τιμή του ύψους 180 αγοριών Ε΄ δημοτικού, μπορούμε να εκτιμήσουμε το ύψος που έχουν όλα τα αγόρια στην ηλικία αυτή;
Αν γνωρίζουμε τη μέση τιμή της θερμοκρασίας ενός τόπου σε χρονικό διάστημα 7 ημερών, μπορούμε να εκτιμήσουμε τη μέση τιμή της θερμοκρασίας του ίδιου τόπου και για τις επόμενες 7 ημέρες; Δικαιολογούμε την απάντησή μας.