
Οι μαθητές και οι μαθήτριες της Ε΄ τάξης φτιάχνουν στο μάθημα των εικαστικών αφίσες και προσκλήσεις για τις εκδηλώσεις τους.
α. Τα κορίτσια φτιάχνουν προσκλήσεις με τα $\dfrac{2}{3}$ του χαρτονιού. Για καθεμιά χρησιμοποιούν το $\dfrac{1}{6}$ του χαρτονιού. Πόσες προσκλήσεις φτιάχνουν;

«Πόσες φορές χωράει …………………………………….»
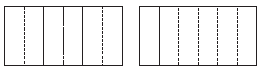

Κάνουμε την πράξη: $\dfrac{2}{3}$÷$\dfrac{1}{6}$ = $\dfrac{4}{6}$ ÷ $\dfrac{1}{6}$ = ⬜ ÷ ⬜ = ⬜.
Άρα τα κορίτσια θα φτιάξουν ………. προσκλήσεις.
β. Τα αγόρια έχουν 3 ίδια χαρτόνια για να φτιάξουν αφίσες. Για καθεμιά χρησιμοποιούν τα $\dfrac{3}{5}$ του χαρτονιού. Πόσες αφίσες φτιάχνουν;
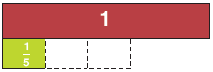

Κάνουμε την πράξη: 3 ÷ $\dfrac{3}{5}$= $\dfrac{ }{5}$ ÷ $\dfrac{3}{5}$ =⬜ ÷ ⬜ = ⬜.
Άρα τα αγόρια θα φτιάξουν ………. αφίσες.
| Βασικές μαθηματικές έννοιες και διεργασίες |
|
Παραδείγματα |
| Για να διαιρέσουμε δυο ομώνυμα κλάσματα, διαιρούμε τους αριθμητές τους. |
|
$\dfrac{3}{5}$ : $\dfrac{4}{5}$ = 3 : 4 = $\dfrac{3}{4}$ , $\dfrac{6}{8}$ : $\dfrac{3}{8}$ = 6 : 3=2 |
| Για να διαιρέσουμε δυο ετερώνυμα κλάσματα, τα μετατρέπουμε πρώτα σε ομώνυμα και έπειτα διαιρούμε τους αριθμητές τους. |
|
$\dfrac{2}{3}$ : $\dfrac{6}{5}$ = $\dfrac{10}{15}$ : $\dfrac{18}{15}$ = 10 : 18 = $\dfrac{10}{18}$ = $\dfrac{5}{9}$ |
| Όταν σε μια διαίρεση οι αριθμοί είναι διαφορετικής μορφής, τους μετατρέπουμε όλους στην ίδια μορφή. |
|
2,5 : 3$\dfrac{1}{2}$ = $\dfrac{25}{10}$ : $\dfrac{7}{2}$ = $\dfrac{25}{10}$ : $\dfrac{35}{10}$ = 25 : 35 = $\dfrac{25}{35}$ = $\dfrac{5}{7}$ |
| Πρόσθετη μαθηματική ιδέα Ένας άλλος τρόπος για να διαιρέσουμε δύο κλάσματα είναι να αντιστρέψουμε τους όρους του δεύτερου κλάσματος και, αντί για διαίρεση, να κάνουμε πολλαπλασιασμό. π.χ. $\dfrac{2}{3}$:$\dfrac{5}{4}$=$\dfrac{2}{3}$ $\text{☓}$ $\dfrac{4}{5}$=$\dfrac{8}{15}$, 6:$\dfrac{3}{4}$=$\dfrac{6}{1}$ $\text{☓}$ $\dfrac{4}{3}$=$\dfrac{6 \text{☓} 4}{3}$=$\dfrac{24}{3}$=8 |
|
Εξήγηση του κανόνα
Ο πολλαπλασιασμός και η διαίρεση είναι αντίστροφες πράξεις: Π.χ. Μοιράζω 6 μπαλόνια σε 3 παιδιά.α. Κάνω διαίρεση: 6 : 3 = 2 μπαλόνια. β. Κάνω πολλαπλασιασμό: Αφού τα παιδιά είναι 3, το καθένα θα πάρει το $\dfrac{1}{3}$ των μπαλονιών: Σημείωση: Ο διαιρετέος μπορεί να είναι και κλάσμα. |

Στη γιορτή της Δανάης οι καλεσμένοι μοιράστηκαν εξίσου τα $\dfrac{3}{4}$ ενός ταψιού με μουσακά. Πόσοι ήταν οι καλεσμένοι, αν κάθε κομμάτι μουσακά ήταν $\dfrac{1}{16}$ του ταψιού;
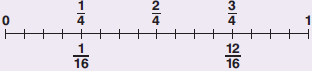
α΄ τρόπος: Με τη βοήθεια της αριθμογραμμής
Στην αριθμογραμμή, από το 0 έως το 1 αντιστοιχεί ολόκληρο το ταψί. Βρίσκουμε τα $\dfrac{3}{4}$. Χωρίζουμε την αριθμογραμμή σε ... ίσα μέρη και παίρνουμε τα .... . Κάθε κομμάτι είναι το $\dfrac{1}{16}$ του ταψιού, γι’ αυτό ξαναχωρίζουμε την αριθμογραμμή σε ... ίσα μέρη. Μετράμε πόσες φορές χωράει το $\dfrac{1}{16}$ είναι στα $\dfrac{3}{4}$. Βρίσκουμε ................. κομμάτια, άρα οι καλεσμένοι είναι 12.
β΄ τρόπος: Δημιουργία ομώνυμων κλασμάτων: $\dfrac{3}{4}$ : $\dfrac{1}{16}$= $\text{—}$ : $\text{—}$ = ...................... καλεσμένοι.
γ΄ τρόπος: Αντιστροφή του διαιρέτη και πολλαπλασιασμός: $\dfrac{3}{4}$ : $\dfrac{1}{16}$ = $\dfrac{3}{4}$ x $\text{—}$ =$\dfrac{48}{ }$= ...................... καλεσμένοι
