Μαθηματικά (Ε' Δημοτικού) - Βιβλίο Μαθητή (Εμπλουτισμένο)
1. Κάθε ξύλινο ράφι της βιβλιοθήκης της τάξης έχει μήκος $\dfrac{2}{3}$μ.
Πόσα μέτρα ξύλου θα χρειαστεί, για να αντικατασταθούν 3 ράφια;
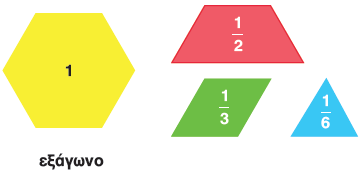
2. Χρησιμοποιούμε τα γεωμετρικά σχήματα του παραρτήματος, για να βρούμε τα παρακάτω γινόμενα, αν το εξάγωνο είναι η ακέραιη μονάδα.
| α. | 3 $\text{☓}$ $\dfrac{1}{2}$= | 4 $\text{☓}$ $\dfrac{1}{2}$= |
| β. | 2 $\text{☓}$ $\dfrac{1}{6}$= | $\dfrac{1}{6}$ $\text{☓}$ 2= |
| γ. | 6 $\text{☓}$ $\dfrac{1}{6}$= | 3 $\text{☓}$ $\dfrac{1}{3}$= |
3. Τα $\dfrac{2}{3}$ ενός οικοπέδου είναι κήπος. Στο $\dfrac{1}{5}$ του κήπου αυτού φυτέψαμε λουλούδια.
Τι μέρος του οικοπέδου καλύπτεται από λουλούδια;
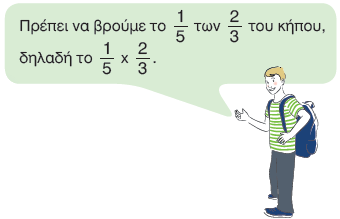
Σχεδιάζουμε στο παραπάνω σχήμα και υπολογίζουμε:
4.Βρίσκουμε τα γινόμενα με τη βοήθεια των μοντέλων αναπαράστασης.
| Βασικές μαθηματικές έννοιες και διεργασίες |
|
Παραδείγματα |
| Στον πολλαπλασιασμό ενός φυσικού αριθμού με ένα κλάσμα, ο φυσικός αριθμός μάς δείχνει πόσες φορές προσθέτω το κλάσμα με τον εαυτό του. Στον πολλαπλασιασμό, αν αλλάξουμε τη σειρά των παραγόντων, το γινόμενο παραμένει το ίδιο. |
|
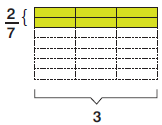
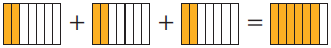 3 $\text{☓}$ $\dfrac{2}{7}$ = $\dfrac{2}{7}$ +$\dfrac{2}{7} + \dfrac{2}{7}$ = $\dfrac{3 \text{☓} 2}{7}$ = $\dfrac{6}{7}$ |
| Το γινόμενο φυσικού αριθμού με κλάσμα ή κλάσματος με φυσικό αριθμό είναι ένα κλάσμα που έχει αριθμητή το γινόμενο του αριθμητή με τον φυ-σικό αριθμό και παρονομαστή τον παρονομαστή του κλάσματος. |
|
$\dfrac{2}{7}$ $\text{☓}$ 3 = 3 $\text{☓}$ $\dfrac{2}{7}$ |
| Όταν ζητάμε ένα μέρος ενός αριθμού, φυσικού ή κλασματικού, κάνουμε πολλαπλασιασμό. |
|
$\dfrac{1}{5}$ $\text{☓}$ $\dfrac{2}{3}$=$\dfrac{1 \text{☓} 2}{5 \text{☓} 3}$=$\dfrac{2}{15}$ Βρίσκουμε το $\dfrac{1}{5}$ του $\dfrac{2}{3}$.
|
| Το γινόμενο δυο κλασμάτων είναι ένα κλάσμα που έχει αριθμητή το γινόμενο των αριθμητών και πα-ρονομαστή το γινόμενο των παρονομαστών. |
|
|
| Αντίστροφοι αριθμοί λέγονται δυο αριθμοί που το γινόμενό τους είναι 1. |
|
$\dfrac{1}{5}$ $\text{☓}$ 5 = $\dfrac{1}{5}$ $\text{☓}$ $\dfrac{5}{1}$ = 1 , $\dfrac{7}{5}$ x $\dfrac{5}{7}$ = $\dfrac{35}{35}$ = 1 |
1. Να βρείτε το $\dfrac{1}{3}$ από το $\dfrac{1}{2}$ μιας σοκολάτας.
α΄ τρόπος: α. Αναπαριστάνουμε τη σοκολάτα με ένα ορθογώνιο. Χρωματίζουμε το $\dfrac{1}{2}$. β. Χωρίζουμε το $\dfrac{1}{2}$ σε 3 ίσα μέρη και από αυτά χρωματίζουμε το 1. γ. Χωρίζουμε όμοια και το υπόλοιπο ορθογώνιο. Παρατηρούμε ότι το $\dfrac{1}{3}$ του $\dfrac{1}{2}$του ορθογωνίου είναι το $\dfrac{1}{6}$ του ορθογωνίου.
β΄ τρόπος: Βρίσκουμε το $\dfrac{1}{3}$ του $\dfrac{1}{2}$ με πολλαπλασιασμό: $\dfrac{1}{3}$ $\text{☓}$ $\dfrac{1}{2}$ = $\dfrac{1\text{☓}1}{3\text{☓}2}$ = $\dfrac{1}{6}$
2. Να βρείτε το γινόμενο 2 x 1 $\dfrac{1}{4}$.
α΄ τρόπος: 2 x 1 $\dfrac{1}{4}$ = 2 x (1 + $\dfrac{1}{4}$ ) = (2 x 1) + (2 $\text{☓}$ $\dfrac{1}{4}$) = 2 + $\dfrac{2}{4}$ = 2 $\dfrac{2}{4}$
β΄ τρόπος: μετατροπή μεικτού σε κλάσμα μεγαλύτερο της μονάδας : 2 $\text{☓}$ 1 $\dfrac{1}{4}$ =2 $\text{☓}$ $\dfrac{5}{4}$ = $\dfrac{10}{4}$ = 2 $\dfrac{2}{4}$
