
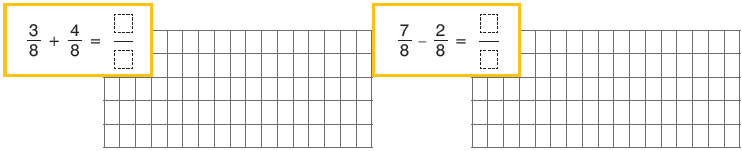
1. Χρησιμοποιούμε το τετραγωνισμένο χαρτί, για να αναπαραστήσουμε με ράβδους ή ορθογώνια τα κλάσματα και να υπολογίσουμε τα αθροίσματα και τις διαφορές:
α. $\dfrac{3}{8}+\dfrac{4}{8}$β. $\dfrac{7}{8}$–$\dfrac{2}{8}$.
2. Χρησιμοποιούμε ράβδους κλασμάτων, για να αναπαραστήσουμε και να υπολογίσουμε αθροίσματα και διαφορές κλασμάτων.
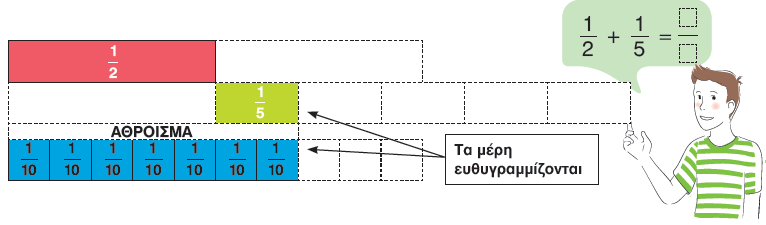
α. Εξηγούμε τον τρόπο με τον οποίο σκέφτηκε ο Νίκος και έπειτα συμπληρώνουμε το άθροισμα.
....................................................................................................................................................
....................................................................................................................................................
β. Θα μπορούσε ο Νίκος, αντί για τις ράβδους $\dfrac{1}{10}$, να χρησιμοποιήσει τις ράβδους $\dfrac{1}{8}$;
Εξηγούμε: ....................................................................................................................................
γ. Χρησιμοποιούμε τις ράβδους για να βρούμε τη διαφορά $\dfrac{3}{4}$ – $\dfrac{1}{8}$.
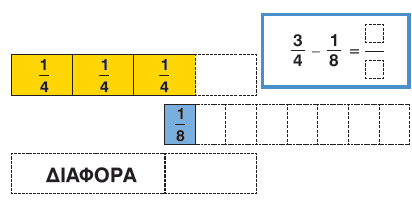
Εξηγούμε τον τρόπο εργασίας μας.
.........................................................
.........................................................
.........................................................
δ.Ποιες άλλες ράβδους θα μπορούσαμε να χρησιμοποιήσουμε για να αναπαραστήσουμε τη διαφορά;...............................................................................................................................................

| Βασικές μαθηματικές έννοιες και διεργασίες |
|
Παραδείγματα |
| Τα κλάσματα που έχουν ίδιο παρονομαστή λέγονται ομώνυμα, ενώ τα κλάσματα που έχουν διαφορετικό παρονομαστή λέγονται ετερώνυμα. |
|
$\dfrac{2}{5}$ , $\dfrac{7}{5}$ $\dfrac{2}{5} , \dfrac{3}{7} , \dfrac{9}{4}$ |
| Για να προσθέσουμε ή να αφαιρέσουμε ετερώνυμα κλάσματα τα μετατρέπουμε πρώτα σε ομώνυμα και στη συνέχεια προσθέτουμε ή αφαιρούμε τους αριθμητές, ενώ παρονομαστή αφήνουμε τον ίδιο. Στο τέλος, κάνουμε απλοποίηση. |
|
|

1. Να βρείτε το άθροισμα: 6$\dfrac{3}{4}$+2$\dfrac{1}{2}$
α΄ τρόπος: Μετατρέπουμε τους μεικτούς αριθμούς σε κλάσματα.
6$\dfrac{3}{4}$ + 2$\dfrac{1}{2}$ =………………………………………………………….……………………………………
β΄ τρόπος: Προσθέτουμε χωριστά τις ακέραιες μονάδες από τα κλάσματα.
6 $\dfrac{3}{4}$+ 2 $\dfrac{1}{2}$ = 8 + $\dfrac{3}{4}$ + $\dfrac{1}{2}$ = ………………………………………………………………………………..
Σε κάθε περίπτωση, στο τέλος, μετατρέπουμε πάλι σε μεικτό αριθμό και, αν γίνεται, κάνουμε και απλοποίηση.
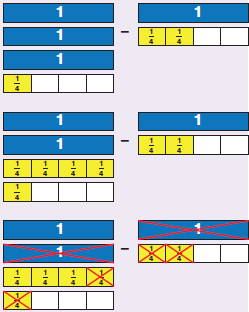
2. Με τη βοήθεια του μοντέλου , να κάνετε την παρακάτω αφαίρεση: 3 $\dfrac{1}{4}$ – 1 $\dfrac{2}{4}$
...................................................................................................
...................................................................................................
...................................................................................................
...................................................................................................
Περιγράφουμε τη διαδικασία: .......................................................
...................................................................................................
...................................................................................................
